Skip to main content

Advertisement

Springer Nature Link
Log in

Extended least squares support vector machines for ordinal regression

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

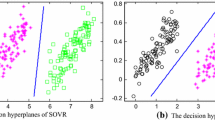
We extend LS-SVM to ordinal regression, which has wide applications in many domains such as social science and information retrieval where human-generated data play an important role. Most current methods based on SVM for ordinal regression suffer from the problem of ignoring the distribution information reflected by the samples clustered around the centers of each class. This problem would degrade the performance of SVM-based methods since the classifiers only depend on the scattered samples on the border which induce large margin. Our method takes the samples clustered around class centers into account and has a competitive computational complexity. Moreover, our method would easily produce the optimal cut-points according to the prior class probabilities and hence may obtain more reasonable results when the prior class probabilities are not the same. Experiments on simulated datasets and benchmark datasets, especially on the real ordinal datasets, demonstrate the effectiveness of our method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Notes

  1. In the original paper [27], the form of the classifier is \(y(x)=\text{ sign }[\omega ^\top \varphi (x)+b]\). Here, we use the classifier \(y(x)=\text{ sign }[\omega ^\top \varphi (x)-b]\) to keep consistence with Sect. 3.

  2. The second term should be \(\alpha ^{\top }DKD\alpha\) after this substitution, but we use \(\Vert \alpha \Vert ^2\) instead for regularization and smoothing purpose as in [36, 39].

  3. Since EBC is a framework of reducing ordinal regression problem to binary classification, the computational complexity varies from \(2N-n_1-n_K\) to KN when the parameters change.

  4. The cut-points in this section are normalized by \(\frac{b_j}{\Vert w\Vert }\).

  5. The datasets are available at http://www.gatsby.ucl.ac.uk/~chuwei/ordinalregression.html.

  6. Because the partition for the first four datasets has been given by Chu, we just use these splits in our experiments for comparison purpose.

  7. The datasets are available at the WEKA website (http://www.cs.waikato.ac.nz/ml/index.html).

References

  1. Hastie T, Tibshirani R, Friedman J (2009) The elements of statistical learning, 2nd edn. Springer, Heidelberg

    Book  MATH  Google Scholar 

  2. Cruz-Ramirez M, Fernandez JC, Valero A, Gutierrez PA, Hervas-Martnez C (2013) Multiobjective Pareto ordinal classification for predictive microbiology. In: Snášel V, Abraham A, Corchado ES (eds) Soft computing models in industrial and environmental applications, Springer, Berlin, Heidelberg, pp 153–162

    Google Scholar 

  3. Kramer S, Widmer G, Pfahringer B, DeGroeve M (2001) Prediction of ordinal classes using regression trees. Fundam Inf 47(1–2):1–13

    MathSciNet  MATH  Google Scholar 

  4. Chu W, Keerthi SS (2007) Support vector ordinal regression. Neural Comput 19:792–815

    Article  MathSciNet  MATH  Google Scholar 

  5. McCullagh P, Nelder JA (1989) Generalized linear models, 2nd edn. Champman and Hall, London

    Book  MATH  Google Scholar 

  6. Crammer K, Singer Y (2002) Pranking with ranking. In: Dietterich TG, Becher S, Ghahramani Z (eds) Advances in neural information processing systems 14, vol 1. MIT Press, Cambridge, pp 641–647

    Google Scholar 

  7. Herbrich R, Graepel T, Obermayer K (2000) Large margin rank boundaries for ordinal regression. Advances in large margin classifiers. MIT Press, Cambridge

    Google Scholar 

  8. Agresti A (2002) Categorical data analysis, 2nd edn. Wiley, New York

    Book  MATH  Google Scholar 

  9. McCullagh P (1980) Regression models for ordinal data. J R Stat Soc Ser B 42:109–142

    MathSciNet  MATH  Google Scholar 

  10. Boser B, Guyon I, Vapnik V (1992) A training algorithm for optimal margin classifier. In: Proceedings of the fifth annual ACM workshop on computational learning research. ACM, pp 144–52

  11. Vapnik V (1998) Statistical learning theory. Wiley, New York

    MATH  Google Scholar 

  12. Cristianini N, Shawe-Taylor J (1999) An introduction to support vector machines. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  13. Gonzalez L, Angulo C, Velasco F, Catala A (2006) Dual unification of bi-class support vector machine formulations. Pattern Recognit 39(7):1325–1332

    Article  MATH  Google Scholar 

  14. Xue H, Chen S, Yang Q (2011) Structural regularized support vector machine: a framework for structural large margin classifier. IEEE Trans Neural Netw 22(4):573–587

    Article  Google Scholar 

  15. Kim S, Park YJ, Toh K, Lee S (2010) SVM-based feature extraction for face recognition. Pattern Recognit 43(8):2871–2881

    Article  MATH  Google Scholar 

  16. Chen Y, Su C, Yang T (2013) Rule extraction from support vector machines by genetic algorithms. Neural Comput Appl 23(3–4):729–739

    Article  Google Scholar 

  17. Rosillo R, Giner J, Fuente D (2014) The effectiveness of the combined use of VIX and support vector machines on the prediction of SP 500. Neural Comput Appl 22(2):321–332

    Google Scholar 

  18. Azar AT, El-Said SA (2014) Performance analysis of support vector machines classifiers in breast cancer mammography recognition. Neural Comput Appl 24(5):1163–1177

    Article  Google Scholar 

  19. Angulo C, Ruiz F, Gonzalez L, Ortega JA (2006) Multi-classification by using tri-class SVM. Neural Process Lett 23:90–101

    Article  Google Scholar 

  20. Shashua A, Levin A (2003) Ranking with large margin principle: two approaches. In: Becker S, Thrun S, Obermayer K (eds) Advances in neural information processing systems 15, MIT Press, Cambridge, pp 961–968

    Google Scholar 

  21. Zhao B, Wang F, Zhang C (2009) Block-quantized support vector ordinal regression. IEEE Trans Neural Netw 20(5):882–890

    Article  Google Scholar 

  22. Pelckmans K, Karsmakers P, Suykens JAK, De Moor B (2006) Ordinal least squares support vector machines—a discriminant analysis approach. In: Proceedings of the machine learning for signal processing (MLSP 2006), pp 1–8

  23. Lin L, Lin HT (2007) Ordinal regression by extended binary classification. In: Advances in neural information processing systems 19. Proceedings of the 2006 Conference (NIPS 2006). MIT Press, pp 865–872

  24. Cardoso JS, Pinto JF (2007) Learning to classify ordinal data: the data replication method. J Mach Learn Res 8:1393–1429

    MathSciNet  MATH  Google Scholar 

  25. Sun BY, Li J, Wu DD (2010) Kernel discriminant learning for ordinal regression. IEEE Trans Knowl Data Eng 22(6):906–910

    Article  Google Scholar 

  26. Kramer KA, Hall LO, Goldgof DB, Remsen A, Luo T (2009) Fast support vector machines for continuous data. IEEE Trans Syst Man Cybern Part B Cybern 39(4):989–1001

    Article  Google Scholar 

  27. Suykens JAK, Vandewalle J (1999) Least squares support vector machine classifiers. Neural Process Lett 9:293–300

    Article  MathSciNet  MATH  Google Scholar 

  28. Suykens JAK, van Gestel T, De Brabanter J (2002) Least squares support vector machines. World Scientific, Singapore

    Book  MATH  Google Scholar 

  29. Van Gestel T, Suykens JAK, Lanckriet G (2002) A Bayesian framework for least squares support vector machine classifiers, gaussian processes and Kernel Fisher discriminant analysis. Neural Comput 14(5):1115–1147

    Article  MATH  Google Scholar 

  30. Adankon MM, Cheriet M (2009) Model selection for the LS-SVM. Application to handwriting recognition. Pattern Recognit 42(12):3264–3270

    Article  MATH  Google Scholar 

  31. Adankon MM, Cheriet M, Biem A (2011) Semisupervised learning using Bayesian interpretation: application to LS-SVM. IEEE Trans Neural Netw 22(4):513–524

    Article  Google Scholar 

  32. Evgeniou T, Pontil M, Poggio T (2001) Regularization networks and support vector machines. Adv Comput Math 13:1–50

    Article  MathSciNet  MATH  Google Scholar 

  33. Williams CKI (1998) Prediction with Gaussian process: from linear regression to linear prediction and beyond. In: Jordan MI (ed) Learning and inference in graphical models. Kluwer Academic Press, Dordrecht

    Google Scholar 

  34. Saunders C, Gammerman A, Vovk V (1998) Ridge regression learning algorithm in dual variables. In: Proceedings of the 15th International Conference on Machine Learning (ICML98), pp 515–521

  35. Van Gestel T, Suykens JAK (2004) Benchmarking least squares support vector machine classifiers. Mach Learn 54:5–32

    Article  MATH  Google Scholar 

  36. Fung G, Mangasarian OL (2001) Proximal support vector machine classifiers. ACM Special Internet Group on Management of Data AAAI, ACM, New York

    Book  MATH  Google Scholar 

  37. Cevikalp H, Neamtu M, Barkana A (2007) The kernel common vector method: a novel nonlinear subspace classifier for pattern recognition. IEEE Trans Syst Man Cybern Part B Cybern 37(4):937–951

    Article  Google Scholar 

  38. Müller K-R, Mika S, Rätsch G (2001) An introduction to kernel-based learning algorithms. IEEE Trans Neural Netw 12(2):181–201

    Article  Google Scholar 

  39. Lee YJ, Mangasarian OL (2001) SSVM: a smooth support vector machine. Comput Optim Appl 20(1):5–22

    Article  MathSciNet  MATH  Google Scholar 

  40. Francis FB, Jordan MI (2005) Predictive low-rank decomposition for kernel methods. In: Proceedings of the 22nd international conference on machine learning (ICML2005), pp 33–40

  41. Gaudette L, Japkowicz N (2009) Evaluation methods for ordinal regression. Canadian AI 2009, LNAI 5549, pp 207–210

  42. Waegeman W, Baetsb BD, Boullarta L (2008) ROC analysis in ordinalregression learning. Pattern Recognit Lett 29(1):1–9

    Article  Google Scholar 

  43. Baccianella S, Esuli A, Sebastiani F (2009) Evaluation measures for ordinal regression. In: 2009 Ninth international conference on intelligent systems design and applications

Download references

Acknowledgments

This research is supported by the Natural Science Foundation of Guangdong Province under grants 2014A030310332 and 2014A030310414.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, College of Mathematics and Informatics, South China Agricultural University, Guangzhou, 510642, China

    Na Zhang

Authors
  1. Na Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Na Zhang.

Appendix: Proof of Proposition 1

Appendix: Proof of Proposition 1

By obtaining the expressions of \(\xi _j^i\) and \(\tilde{\xi }_j^i\) from the equality constraint of (11) and substituting them for \(\xi _j^i\) and \(\tilde{\xi }_j^i\) in (10), the QP problem of (10) and (11) is converted to

$$\min _{\omega , b}{\mathcal {J}}(\omega , b)=\frac{1}{2}\left[ \sum _{j=1}^{K-1}\sum _{i\in \mathcal {I}_j}{(\omega ^\top x_i-b_j+1)^2}+\sum _{j=1}^{K-1}\sum _{i\in \mathcal {I}_{j+1}}{(-\omega ^\top x_i+b_j+1)^2}\right] +\frac{\lambda }{2}\Vert \omega \Vert ^2$$
(26)

subject to

$$b_1\le b_2\le \ldots \le b_{K-1}.$$
(27)

Define the following Lagrangian equation:

$${\mathcal {L}}(\omega ,b;\eta )={\mathcal {J}}(\omega ,b) -\sum _{j=1}^{K-2}{\eta _j(b_{j+1}-b_j)},$$
(28)

with Lagrange multipliers \(\eta _j\ge 0\). From the condition \(\frac{\partial {{\mathcal {L}}}}{\partial {b_j}}=0\) we get

$$\sum _{i\in \mathcal {I}_j}-(\omega ^\top x_i-b_j+1)+\sum _{i\in \mathcal {I}_{j+1}}(-\omega ^\top x_i+b_j+1)+\eta _j-\eta _{j-1}=0,$$
(29)

where \(\eta _0=0\). Since \(b_1<b_2<\ldots <b_{K-1}\), from KKT conditions, we get \(\eta _j=0\) for \(j=1,2,\ldots ,K-2\). Therefore, from Eq. (29) we can obtain Eq. (12).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, N. Extended least squares support vector machines for ordinal regression. Neural Comput & Applic 27, 1497–1509 (2016). https://doi.org/10.1007/s00521-015-1948-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-015-1948-2

Keywords