Skip to main content
Springer Nature Link
Log in

Stability in distribution of stochastic delay recurrent neural networks with Markovian switching

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

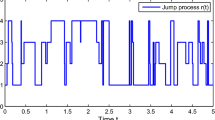
This paper investigates the stability in distribution of stochastic delay recurrent neural networks with Markovian switching. Using Lyapunov function and stochastic analysis techniques, sufficient conditions on the stability in distribution are given. For such recurrent neural networks, it reveals that the limit distribution of transition probability for segment process associated with solution process is indeed a unique ergodic invariant probability measure. Moreover, a numerical example is also provided to demonstrate the effectiveness and applicability of the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Haykin S (1994) Neural networks. Prentice-Hall, Upper Saddle River

    MATH  Google Scholar 

  2. Liu D, Michel A (1993) Celluar neural networks for associative memories. IEEE Trans Circuits Syst II 40(2):119–121

    Article  MathSciNet  Google Scholar 

  3. Arik S (2000) Stability analysis of delayed neural networks. IEEE Trans Circuits Syst I 47(7):1089–1092

    Article  MathSciNet  MATH  Google Scholar 

  4. Hirasawa K, Mabu S, Hu J (2006) Propagation and control of stochastic signals through universal learning networks. Neural Netw 19(4):487–499

    Article  MATH  Google Scholar 

  5. Cao J, Wang J (2004) Absolute exponential stability of recurrent neural networks with Lipschitz-continuous activation functions and time delays. Neural Netw 17(3):379–390

    Article  MATH  Google Scholar 

  6. Li L, Huang L (2009) Dynamical behaviors of a class of recurrent neural networks with discontinuous neuron activations. Appl Math Model 33(12):4326–4336

    Article  MathSciNet  MATH  Google Scholar 

  7. Huang Y, Zhang H, Wang Z (2012) Dynamical stability analysis of multiple equilibrium points in time-varying delayed recurrent neural networks with discontinuous activation functions. Neurocomputing 91:21–28

    Article  Google Scholar 

  8. Wan L, Sun J (2005) Mean square exponential stability of stochastic delayed Hopfield neural networks. Phys Lett A 343(4):306–318

    Article  MATH  Google Scholar 

  9. Sun Y, Cao J (2007) pth moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Anal Real 8(4):1171–1185

    Article  MathSciNet  MATH  Google Scholar 

  10. Huang C, He Y, Huang L, Zhu W (2008) pth moment stability analysis of stochastic recurrent neural networks with time-varying delays. Inf Sci 178(9):2194–2203

    Article  MathSciNet  MATH  Google Scholar 

  11. Ma L, Da F (2009) Mean-square exponential stability of stochastic Hopfield neural networks with time-varying discrete and distributed delays. Phys Lett A 373(25):2154–2161

    Article  MathSciNet  MATH  Google Scholar 

  12. Li B, Xu D (2009) Mean square asymptotic behavior of stochastic neural networks with infinitely distributed delays. Neurocomputing 72(13–15):3311–3317

    Article  Google Scholar 

  13. Chen W, Zheng W (2010) Robust stability analysis for stochastic neural networks with time-varying delay. IEEE Trans Neural Netw 21(3):508–514

    Article  Google Scholar 

  14. Song Q (2011) Stochastic dissipativity analysis on discrete-time neural networks with time-varying. Neurocomputing 74(5):838–845

    Article  Google Scholar 

  15. Wang Z, Liu Y, Liu X (2006) Exponential stability of delayed recurrent neural networks with Markovian jumping parameters. Phys Lett A 356(4–5):346–352

    Article  MATH  Google Scholar 

  16. Lou X, Cui B (2007) Delay-dependent stochastic stability of delayed Hopfield neural networks with Markovian jump parameters. J Math Anal Appl 328(1):316–326

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu Y, Wang Z, Liu X (2008) On delay-dependent robust exponential stability of stochastic neural networks with mixed time delays and Markovian switching. Nonlinear Dyn 54(3):199–212

    Article  MathSciNet  MATH  Google Scholar 

  18. Liu Y, Wang Z, Liang J, Liu X (2009) Stability and synchronization of discrete-time Markovian jumping neural networks with mixed mode-dependent time delays. IEEE Trans Neural Netw 20(7):1102–1116

    Article  Google Scholar 

  19. Shen Y, Wang J (2009) Almost sure exponential stability of recurrent neural networks with Markov switching. IEEE Trans Neural Netw 20(5):840–855

    Article  Google Scholar 

  20. Wu Z, Su H, Chu J (2010) State estimation for discrete Markovian jumping neural networks with delay. Neurocomputing 73(10–12):2247–2254

    Article  Google Scholar 

  21. Zhu E, Zhang H, Zou J (2010) Stability analysis of recurrent neural networks with random delay and Markovian switching. J. Inequal. Appl. 2010, Article ID 191546, 12 pages

  22. Balasubramaniam P, Lakshmanan S (2010) State estimation for Markovian jumping recurrent neural networks with interval time-varying delays. Nonlinear Dyn 60(4):661–675

    Article  MathSciNet  MATH  Google Scholar 

  23. Chen Y, Zheng W (2012) Stochastic state estimation for neural networks with distributed delays and Markovian jump. Neural Netw 25:14–20

    Article  MathSciNet  MATH  Google Scholar 

  24. Liao X, Mao X (1996) Exponential stability and instability of stochastic neural networks. Stoch Anal Appl 14(2):165–185

    Article  MathSciNet  MATH  Google Scholar 

  25. Tino P, Cernansky M, Benuskova L (2004) Markovian architectural bias of recurrent neural networks. IEEE Trans Neural Netw 15(1):6–15

    Article  Google Scholar 

  26. Mao X, Yuan C (2006) Stochastic differential equations with Markovian switching. Imperial College Press, London

    Book  MATH  Google Scholar 

  27. Basak G, Bisi A, Ghosh M (1996) Stability of a random diffusion with linear drift. J Math Anal Appl 202(2):604–622

    Article  MathSciNet  MATH  Google Scholar 

  28. Yuan C, Mao X (2003) Asymptotic stability in distribution of stochastic differential equations with Markovian switching. Stoch Process Appl 103(2):277–291

    Article  MathSciNet  MATH  Google Scholar 

  29. Yuan C, Zou J, Mao X (2003) Stability in distribution of stochastic differential delay equations with Markovian switching. Syst Control Lett 50(3):195–207

    Article  MathSciNet  MATH  Google Scholar 

  30. Bao J, Hou Z, Yuan C (2009) Stability in distribution of neutral stochastic differential delay equations with Markovian switching. Stat Probabil Lett 79(15):1663–1673

    Article  MathSciNet  MATH  Google Scholar 

  31. Hu G, Wang K (2012) Stability in distribution of neutral stochastic functional differential equations with Markovian switching. J Math Anal Appl 385(2):757–769

    Article  MathSciNet  MATH  Google Scholar 

  32. Mao X, Matasov A, Pinunovskiy A (2000) Stochastic differential delay equations with Markovian switching. Bernoulli 6(1):73–90

    Article  MathSciNet  MATH  Google Scholar 

  33. Bao J, Yin G, Yuan C, Wang L (2014) Exponential ergodicity for retarded stochastic differential equations. Appl Anal 93(11):2330–2349

    Article  MathSciNet  MATH  Google Scholar 

  34. Bao J, Yuan C (2014) Numerical approximation of stationary distributions for stochastic partial differential equations. J Appl Probab 51(3):858–873

    Article  MathSciNet  MATH  Google Scholar 

  35. Bao J, Yin G, Yuan C (2014) Ergodicity for functional stochastic differential equations and applications. Nonlinear Anal 98:66–82

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China under Grants Nos.11101054, 11272067, Hunan Provincial Natural Science Foundation of China under Grant No. 12JJ4005, the Scientific Research Funds of Hunan Provincial Education Department of China under Grant No.13C1036, Humanities and Social Sciences Foundation of Ministry of Education of China under Grants No. 12YJAZH173 and the National Social Science Foundation of China under Grant No.15BJY12.

Author information

Authors and Affiliations

  1. School of Mathematics and Computing Science, Changsha University of Science and Technology, Changsha, 410004, Hunan, People’s Republic of China

    Enwen Zhu

  2. Department of Mathematics, Wayne State University, Detroit, MI, 48202, USA

    George Yin

  3. Department of Mathematics, Statistics and Computer Science, University of Wisconsin-Stout, Menomonie, WI, 54751, USA

    Quan Yuan

Authors
  1. Enwen Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. George Yin
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Quan Yuan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Enwen Zhu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhu, E., Yin, G. & Yuan, Q. Stability in distribution of stochastic delay recurrent neural networks with Markovian switching. Neural Comput & Applic 27, 2141–2151 (2016). https://doi.org/10.1007/s00521-015-2013-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-015-2013-x

Keywords