Neural identifier for unknown discrete-time nonlinear delayed systems

Abstract

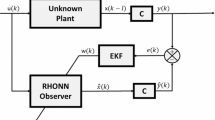
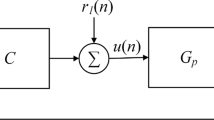
This work proposes a discrete-time nonlinear neural identifier based on a recurrent high-order neural network trained with an extended Kalman filter-based algorithm for discrete-time deterministic multiple-input multiple-output systems with unknown dynamics and time-delay. To prove the semi-globally uniformly ultimately boundedness of the proposed neural identifier, the stability analysis based on the Lyapunov approach is included. Applicability of the proposed identifier is shown via simulation and experimental results, all of them performed under the presence of unknown external and internal disturbances as well as unknown time-delays.

Appendix

Proof of Theorem 1

Step 1, for ${\mathbf {V}}\left( k\right)$. First consider, the equation for each i-th neuron $(i=1,...,n)$

$$\begin{aligned} V_{i}\left( k\right)= & \, \gamma _{i}e_{i}^{2}\left( k\right) +\widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \nonumber \\ \Delta V_{i}\left( k\right)= & \, V\left( k+1\right) -V\left( k\right) \nonumber \\= & \, \gamma _{i}e_{i}^{2}\left( k+1\right) \nonumber \\&+\,\widetilde{w}_{i}^{T}\left( k+1\right) P_{i}\left( k+1\right) \widetilde{w}_{i}\left( k+1\right) \nonumber \\&-\,\widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) -\gamma _{i}e_{i}^{2}\left( k\right) \end{aligned}$$

(23)

Using (10) and (14) in (23)

$$\begin{aligned} \Delta V_{i}\left( k\right)= & \,\left[ \widetilde{w}_{i}\left( k\right) -\eta _{i}K_{i}\left( k\right) e_{i}\left( k\right) \right] ^{T}[P_{i}\left( k\right) -A_{i}\left( k\right) ] \\ \times&\left[ \widetilde{w}_{i}\left( k\right) -\eta _{i}K_{i}\left( k\right) e_{i}\left( k\right) \right] \\&+\,\gamma _{i}\left[ \widetilde{w}_{i}\left( k\right) z_{i}\left( x(k-l),u(k)\right) +\epsilon _{z_{i}}\right] ^{2} \\&-\,\widetilde{w}_{i}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) -\gamma _{i}e_{i}^{2}\left( k\right) \end{aligned}$$

(24)

with

$$A_{i}\left( k\right) =K_{i}\left( k\right) H_{i}^{\top }\left( k\right) P_{i}\left( k\right) +Q_{i}\left( k\right)$$

(25)

then, (24) can be expressed as

$$\begin{aligned} \Delta V_{i}\left( k\right)= & \, \widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&-\,\eta _{i}e_{i}\left( k\right) K_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&-\,\widetilde{w}_{i}^{T}\left( k\right) A_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&+\,\eta _{i}e_{i}\left( k\right) K_{i}^{T}\left( k\right) A_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&-\,\eta _{i}e_{i}\left( k\right) \widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) K_{i}\left( k\right) \\&+\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) P_{i}\left( k\right) K_{i}\left( k\right) \\&+\,\eta _{i}e_{i}\left( k\right) \widetilde{w}_{i}^{T}\left( k\right) A_{i}\left( k\right) K_{i}\left( k\right) \\&-\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) A_{i}\left( k\right) K_{i}\left( k\right) \\&+\,\gamma _{i}\left( \widetilde{w}_{i}\left( k\right) z_{i}\left( x(k-l),u(k)\right) \right) ^{2} \\&+\,\gamma _{i}2\epsilon _{z_{i}}\widetilde{w}_{i}\left( k\right) z_{i}\left( x(k),u(k)\right) \\&+\,\gamma _{i}\epsilon _{z_{i}}^{2}-\widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) -\gamma _{i}e_{i}^{2}\left( k\right) \end{aligned}$$

(26)

Using the inequalities

$$\begin{aligned} X^{T}X+Y^{T}Y\ge & 2X^{T}Y \\ X^{T}X+Y^{T}Y\ge & -2X^{T}Y \\ -\lambda _{\min }\left( P\right) X^{2}\ge & -X^{T}PX\ge -\lambda _{\max }\left( P\right) X^{2} \end{aligned}$$

(27)

which are valid $\forall X,Y\in \mathfrak {R}^{n}$, $\forall P\in \mathfrak {R}^{n\times n}, P=P^{T}>0,$ then (26) can be rewritten as

$$\begin{aligned} \Delta V_{i}\left( k\right)\le & -\widetilde{w}_{i}^{T}\left( k\right) A_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&-\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) A_{i}\left( k\right) K_{i}\left( k\right) \\&+\,\widetilde{w}_{i}^{T}\left( k\right) \widetilde{w}_{i}\left( k\right) +e_{i}^{2}\left( k\right) \\&+\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) P_{i}\left( k\right) P_{i}^{T}\left( k\right) K_{i}\left( k\right) \\&+\,\eta _{i}^{2}\widetilde{w}_{i}^{T}A_{i}\left( k\right) K_{i}\left( k\right) K_{i}^{T}\left( k\right) A_{i}^{T}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&+\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) P_{i}\left( k\right) K_{i}\left( k\right) \\&+\,2\gamma _{i}\left( \widetilde{w}_{i}\left( k\right) z_{i}\left( x(k-l),u(k)\right) \right) ^{2} \\&+\,2\gamma _{i}\epsilon _{z_{i}}^{2}-\gamma _{i}e_{i}^{2}\left( k\right) \end{aligned}$$

(28)

Then,

$$\begin{aligned} \Delta V_{i}\left( k\right)\le & -\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}\lambda _{\min }\left( A_{i}\left( k\right) \right) \\&-\,\eta _{i}^{2}\left| e_{i}\left( k\right) \right| ^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\min }\left( A_{i}\left( k\right) \right) \\&+\,\eta _{i}^{2}\left| e_{i}\left( k\right) \right| ^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\max }^{2}\left( P_{i}\left( k\right) \right) \\&+\,2\eta _{i}^{2}\left| e_{i}\left( k\right) \right| ^{2}\left\| K_{i}\left( k\right) \right\| ^{2} \\&+\,\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}\lambda _{\max }\left( P_{i}\left( k\right) \right) \\&+\,\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}\lambda _{\max }^{2}\left( A_{i}\left( k\right) \right) \\&+\,2\gamma _{i}\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}\left\| z_{i}\left( x(k-l),u(k)\right) \right\| ^{2} \\&+\,2\gamma _{i}\epsilon _{z_{i}}^{2}-\gamma _{i}\left| e_{i}\left( k\right) \right| ^{2} \end{aligned}$$

(29)

Defining

$$\begin{aligned} E_{i}\left( k\right)= & \,\lambda _{\min }\left( A_{i}\left( k\right) \right) -\lambda _{\max }^{2}\left( A_{i}\left( k\right) \right) \\&-\,2\gamma _{i}\left\| z_{i}\left( x(k-l),u(k)\right) \right\| ^{2}+\lambda _{\max }\left( P_{i}\left( k\right) \right) \\ F_{i}\left( k\right)= & \,\gamma _{i}+\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\min }\left( A_{i}\left( k\right) \right) \\&-\,\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\max }^{2}\left( P_{i}\left( k\right) \right) -2\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2} \end{aligned}$$

and selecting $\eta _{i}$, $\gamma _{i}$, $Q_{i}$ and $R_{i}$, such that $E_{i}>0$ and $F_{i}>0$, $\forall k$, then, (29) can be expressed as

$$\begin{aligned} \Delta {V_i}\left( k \right) \le- & {\left\| {{{\tilde{\omega }}_i}\left( k \right) } \right\| ^2}{E_i}\left( k \right) - {\left| {{e_i}\left( k \right) } \right| ^2}{F_i}\left( k \right) \\+ &\, 2{\gamma _i}\delta \varepsilon _{{z_i}}^2 \end{aligned}$$

(30)

Hence, $\Delta V_{i}\left( k\right) <0$ when

$$\left\| \widetilde{w}_{i}\left( k\right) \right\| >\sqrt{\frac{2\gamma _{i}\epsilon _{z_{i}}^{2}}{E_{i}\left( k\right) }}\equiv \kappa _{1}$$

(31)

or

$$\left| e_{i}\left( k\right) \right| >\sqrt{\frac{2\gamma _{i}\epsilon _{z_{i}}^{2}}{F_{i}\left( k\right) }}\equiv \kappa _{2}$$

(32)

Step 2. Now for ${\mathbf {V}}\left( k\right)$, consider the Lyapunov function candidate.

$$\begin{aligned} {\mathbf {V}}\left( k\right)= & \, \sum \limits _{i=1}^{n}\widetilde{w} _{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) +\gamma _{i}e_{i}^{2}\left( k\right) \\ \Delta {\mathbf {V}}\left( k\right)= &\, \sum \limits _{i=1}^{n}\left( \widetilde{w }_{i}^{T}\left( k+1\right) P_{i}\left( k+1\right) \widetilde{w}_{i}\left( k+1\right) \right. \\&\left. +\,\gamma _{i}e_{i}^{2}\left( k+1\right) -\widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \right. \\&\left. -\,\gamma _{i}e_{i}^{2}\left( k\right) \right) \end{aligned}$$

(33)

Using (10) and (14) in (23)

$$\begin{aligned} \Delta {\mathbf {V}}\left( k\right)= &\, \sum \limits _{i=1}^{n}\left( \left[ \widetilde{w}_{i}\left( k\right) -\eta _{i}K_{i}\left( k\right) e_{i}\left( k\right) \right] ^{T}\right. \\ \times &\,[P_{i}\left( k\right) -A_{i}\left( k\right) ]\left[ \widetilde{w}_{i}\left( k\right) -\eta _{i}K_{i}\left( k\right) e_{i}\left( k\right) \right] \\&+\,\gamma _{i}\left[ \widetilde{w}_{i}\left( k\right) z_{i}\left( x(k-l),u(k)\right) +\epsilon _{z_{i}}\right] ^{2} \\&\left. -\,\widetilde{w}_{i}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) -\gamma _{i}e_{i}^{2}\left( k\right) \right) \end{aligned}$$

(34)

Defining

$$\begin{aligned} A_{i}\left( k\right)= & \,K_{i}\left( k\right) H_{i}^{\top }\left( k\right) P_{i}\left( k\right) +Q_{i}\left( k\right) \\ E_{i}\left( k\right)= & \,\lambda _{\min }\left( A_{i}\left( k\right) \right) -\lambda _{\max }^{2}\left( A_{i}\left( k\right) \right) \\&-\,2\gamma _{i}\left\| z_{i}\left( x(k-l),u(k)\right) \right\| ^{2}+\lambda _{\max }\left( P_{i}\left( k\right) \right) \\ F_{i}\left( k\right)= & \,\gamma _{i}+\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\min }\left( A_{i}\left( k\right) \right) \\&-\,\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\max }^{2}\left( P_{i}\left( k\right) \right) -2\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2} \end{aligned}$$

and selecting $\eta _{i}$, $\gamma _{i}, Q_{i}$ and $R_{i}$, such that $E_{i}>0$ and $F_{i}>0$, $\forall k$, then, (24) can be expressed as

$$\begin{aligned} \Delta {\mathbf {V}}\left( k\right)\le & \sum \limits _{i=1}^{n}(-\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}E_{i}\left( k\right) \\&- \,\left| e_{i}\left( k\right) \right| ^{2}\left( k\right) F_{i}\left( k\right) +2\gamma _{i}\epsilon _{z_{i}}^{2}) \end{aligned}$$

Hence, $\Delta {\mathbf {V}}\left( k\right) <0$ when (31) or (32) is fulfilled

Therefore, considering Step 1 and Step 2 for (23), the solution of (10) and (14) is SGUUB. $\square$

Remark 1

Considering Theorem 1 and its proof, it can be easily shown that the result can be extended to a system (12) with multiple delays like $x\left( k-l_{i}\right)$ with $i=1,2,\ldots$, can be used instead of $x\left( k-l\right)$ in (3) and/or for time-varying delays $x\left( k-l_{i}\left( k\right) \right)$ with $l_{i}\left( k\right)$ bounded by $l_{i}\left( k\right) \le l$.