Abstract
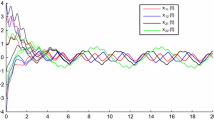
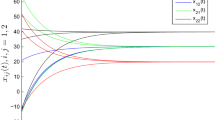
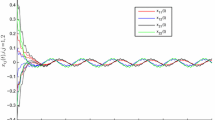
In this paper, the finite-time stability for a class of shunting inhibitory cellular neural networks with neutral proportional delays is discussed. By employing differential inequality techniques, several sufficient conditions are obtained to ensure the finite-time stability for the considered neural networks. Meanwhile, the generalized exponential synchronization is also established. An example along with its numerical simulation is presented to demonstrate the validity of the proposed results.


Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Hien LV (2014) An explicit criterion for finite-time stability of linear nonautonomous systems with delays. Appl Math Lett 30:12–18
Erneux T (2009) Applied delay differential equations. Springer, New York
Phat VN, Hien LV (2009) An application of Razumikhin theorem to exponential stability for linear non-autonomous systems with time-varying delay. Appl Math Lett 22:1412–1417
Ngoc PHA (2012) On exponential stability of nonlinear differential systems with time-varying delay. Appl Math Lett 25:1208–1213
Song B, Park JH, Wu ZG, Zhang Y (2013) New results on delay-dependent stability analysis for neutral stochastic delay systems. J Franklin Inst 350:840–852
Seuret A, Gouaisbaut F (2013) Wirtinger-based integral inequality: application to time-delay systems. Automatica 49:2860–2866
Bouzerdoum A, Pinter RB (1993) Shunting inhibitory cellular neural networks: derivation and stability analysis. IEEE Trans Circuits Syst 1 Fundam Theory Appl 40:215–221
Bouzerdoum A, Pinter RB (1991) Analysis and analog implementation of directionally sensitive shunting inhibitory cellular neural networks. Visual Inf Process Neurons Chips SPIE 1473:29–38
Bouzerdoum A, Pinter RB (1992) Nonlinear lateral inhibition applied to motion detection in the fly visual system. In: Pinter RB, Nabet B (eds) Nonlinear Vision. CRC Press, Boca Raton, pp 423–450
Chen Z (2013) A shunting inhibitory cellular neural network with leakage delays and continuously distributed delays of neutral type. Neural Comput Appl 23:2429–2434
Liu B (2015) Pseudo almost periodic solutions for neutral type CNNs with continuously distributed leakage delays. Neurocomputing 148:445–454
Liu X (2015) Exponential convergence of SICNNs with delays and oscillating coefficients in leakage terms. Neurocomputing 168:500–504
Zhao C, Wang Z (2015) Exponential convergence of a SICNN with leakage delays and continuously distributed delays of neutral type. Neural Process Lett. 41:239–247
Ockendon JR, Tayler AB (1971) The dynamics of a current collection system for an electric locomotive. Proc R Soc A 322:447–468
Fox L, Mayers DF, Ockendon JR, Tayler AB (1971) On a functional-differential equation. J Inst Math Appl 8(3):271–307
Derfel GA (1982) On the behaviour of the solutions of functional and functional-differential equations with several deviating arguments. Ukr Math J 34:286–291
Derfel GA (1990) Kato problem for functional-differential equations and difference Schrödinger operators. Oper Theory 46:319–321
Ockendon JR, Tayler AB (1971) The dynamics of a current collection system for an electric locomotive. Proc R Soc A 322:447–468
Fox L, Mayers DF, Ockendon JR, Tayler AB (1971) On a functional-differential equation. J Inst Math Appl 8(3):271–307
Derfel GA (1982) On the behaviour of the solutions of functional and functional-differential equations with several deviating arguments. Ukr Math J 34:286–291
Song X, Zhao P, Xing Z, Peng J (2016) Global asymptotic stability of CNNs with impulses and multi-proportional delays. Appl Sci Math Methods 39:722–733
Derfel GA (1990) Kato problem for functional-differential equations and difference Schrödinger operators. Oper Theory 46:319–321
Karafyllis I (2006) Finite-time global stabilization by means of time-varying distributed delay feedback. SIAM J Control Optim 45:320–342
Moulay E, Dambrine M, Yeganefar N, Perruquetti W (2008) Finite-time stability and stabilization of time-delay systems. Syst Control Lett 57:561–566
Yang R, Wang Y (2012) Finite-time stability and stabilization of a class of nonlinear time-delay systems. SIAM J Control Optim 50(5):3113–3131
Yang R, Wang Y (2013) Finite-time stability analysis and H control for a class of nonlinear time-delay Hamiltonian systems. Automatica 49:390–401
Efimov D, Polyakov A, Fridman E, Perruquetti W, Richard JP (2014) Comments on finite-time stability of time-delay systems. Automatica 50:1944–1947
Amato F, Ambrosino R, Ariola M, Cosentino C, De Tomasi G (2014) Finite-time stability and control. Springer, London
Garcia G, Tarbouriech S, Bernussou J (2009) Finite-time stabilization of linear time-varying continuous systems. IEEE Trans Autom Control 54:364–369
Amato F, Ariola M, Cosentino C (2010) Finite-time control of discrete-time linear systems: analysis and design conditions. Automatica 46:919–924
Yu Y (2016) Finite-time stability on a class of non-autonomous SICNNs with multi-proportional delays. Asian J Control. doi:10.1002/asjc.1323
Liu B (2016) Finite-time stability of CNNs with neutral proportional delays and time-varying leakage delays. Appl Sci Math Methods. doi:10.1002/mma.3976
Hien L, Son DT (2015) Finite-time stability of a class of non-autonomous neural networks with heterogeneous proportional delays. Appl Math Comput 251:14–23
Chen T, Wang L (2007) Power-rate global stability of dynamical systems with unbounded time-varying delays. IEEE Trans Circuits Syst II Express Briefs 54(8):705–709
Chen T, Wang L (2007) Global \(\mu\)-stability of delayed neural networks with unbounded time-varying delays. IEEE Trans Neural Netw 18(8):1836–1840
Wang L, Chen T (2014) Multiple \(\mu\)-stability of neural networks with unbounded time-varying delays. Neural Netw 53:109–118
Acknowledgments
The author thanks for the anonymous referees valuable opinions. The suggestions improve this paper and motivate some further works.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by the Natural Scientific Research Fund of Hunan Provincial of China (Grant Nos. 2016JJ6103, 2016JJ6104), and the Construction Program of the Key Discipline in Hunan University of Arts and Science−Applied Mathematics.
Rights and permissions
About this article
Cite this article
Yu, Y. Finite-time stability on a class of SICNNs with neutral proportional delays. Neural Comput & Applic 28 (Suppl 1), 97–105 (2017). https://doi.org/10.1007/s00521-016-2295-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-016-2295-7