Skip to main content

Advertisement

Springer Nature Link
Log in

pth Moment synchronization of Markov switched neural networks driven by fractional Brownian noise

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

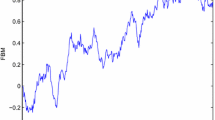
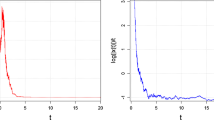
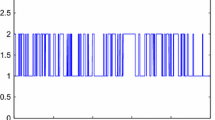
This paper deals with the pth moment synchronization problem for a type of the stochastic neural networks with Markov switched parameters and driven by fractional Brownian noise (FBNSNN). A method called time segmentation method, very different to the Lyapunov functional approach, has been presented to solve the above problem. Meanwhile, based on the trajectory of error system, associating with infinitesimal operator theory, we propose a sufficient condition of consensus for the drive–response system. The criterion of pth moment exponential stability for FBNSNN can guarantee the synchronization under the designed controller. Finally, two numerical examples and some illustrative figures are provided to show the feasibility and effectiveness for our theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Zhang W, Li C, Huang T, Xiao M (2015) Synchronization of neural networks with stochastic perturbation via aperiodically intermittent control. Neural Netw 71:105–111

    Article  Google Scholar 

  2. Wu Z, Shi P, Su H, Chu J (2014) Local synchronization of chaotic neural networks with sampled data and saturating actuators. IEEE Trans Cybern 44(12):2635–2645

    Article  Google Scholar 

  3. Ding S, Wang Z (2015) Stochastic exponential synchronization control of memristive neural networks with multiple time-varying delays. Neurocomputing 162:16–25

    Article  Google Scholar 

  4. Zhou X, Zhou W, Yang J (2015) A novel scheme for synchronization control of stochastic neural networks with multiple time-varying delays. Neurocomputing 159:50–57

    Article  Google Scholar 

  5. Wei Q, Liu D, Lewis FL (2015) Optimal distributed synchronization control for continuous-time heterogeneous multi-agent differential graphical games. Inf Sci 317:96–113

    Article  Google Scholar 

  6. Song Y, Wen S (2015) Synchronization control of stochastic memristor-based neural networks with mixed delays. Neurocomputing 156(25):121–128

    Article  Google Scholar 

  7. Zhou W, Zhu Q, Shi P, Su H, Fang Jianan, Zhou Liuwei (2014) Adaptive synchronization for neutral-type neural networks with stochastic perturbation and Markovian switching parameters. IEEE Trans Cybern 44(12):2848–2860

    Article  Google Scholar 

  8. Zhou X, Zhou W, Yang J (2015) Stochastic synchronization of neural networks with multiple time-varying delays and Markovian jump. J Frankl Inst 352(3):1265–1283

    Article  MathSciNet  MATH  Google Scholar 

  9. Ma Y, Zheng Y (2015) Projective lag synchronization of Markovian jumping neural networks with mode-dependent mixed time-delays based on an integral sliding mode controller. Neurocomputing 168:626–636

    Article  Google Scholar 

  10. Tong D, Zhou W, Zhou X (2015) Exponential synchronization for stochastic neural networks with multi-delayed and Markovian switching via adaptive feedback control. Commun Nonlinear Sci Numer Simul 29:359–371

    Article  MathSciNet  Google Scholar 

  11. Wu Z, Shi P, Su H, Chu J (2013) Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled data. IEEE Trans Cybern 43(6):1796–1806

    Article  Google Scholar 

  12. Yang J, Zhou W, Shi P, Yang X, Zhou Xianghui, Hongye Su (2015) Adaptive synchronization of delayed Markovian switching neural networks with Lévy noise. Neurocomputing 156(25):231–238

    Article  MATH  Google Scholar 

  13. Wu Z, Park JH, Su H, Chu J (2012) Passivity analysis of Markov jump neural networks with mixed time-delays and piecewise-constant transition rates. Nonlinear Anal Real World Appl 13(5):2423–2431

    Article  MathSciNet  MATH  Google Scholar 

  14. Mao X, Shen Y, Yuan C (2008) Almost surely asymptotic stability of neutral stochastic differential delay equations with Markovian switching. Stoch Process Appl 118:1385–1406

    Article  MathSciNet  MATH  Google Scholar 

  15. Wang T, Zhao S, Zhou W, Yu W (2015) Finite-time state estimation for delayed Hopfield neural networks with Markovian jump. Neurocomputing 156(25):193–198

    Article  Google Scholar 

  16. Ksendal B (2005) Stochastic differential equations, 6th edn. Springer, Berlin

    Google Scholar 

  17. Mao X, Yuan C (2006) Stochastic differential equations with Markovian switching. Imperial College Press, London

    Book  MATH  Google Scholar 

  18. Wang Z, Liu Y, Li M (2006) Stability analysis for stochastic Cohen–Grossberg neural networks with mixed time delays. IEEE Trans Neural Netw 17:814–820

    Article  Google Scholar 

  19. Zhou X, Zhou W, Dai A, Yang J (2014) Asymptotical stability of stochastic neural networks with multiple time-varying delays. Int J Control 88(3):613–621

    Article  MathSciNet  MATH  Google Scholar 

  20. Chen H, Zhao Y (2015) Delay-dependent exponential stability for uncertain neutral stochastic neural networks with interval time-varying delay. Int J Syst Sci 46(14):2584–2597

    Article  MathSciNet  MATH  Google Scholar 

  21. Wang Z, Shu H, Fang J (2006) Robust stability for stochastic Hopfield neural networks with time delays. Nonlinear Anal Real World Appl 7(5):1119–1128

    Article  MathSciNet  MATH  Google Scholar 

  22. Yang L, Li Y (2015) Existence and exponential stability of periodic solution for stochastic Hopfield neural networks on time scales. Neurocomputing 167:543–550

    Article  Google Scholar 

  23. Peng J, Liu Z (2011) Stability analysis of stochastic reaction–diffusion delayed neural networks with Lévy noise. Neural Comput Appl 20(4):535–541

    Article  Google Scholar 

  24. Yang J, Zhou W, Shi P (2015) Synchronization of delayed neural networks with Lévy noise and Markovian switching via sampled data. Nonlinear Dyn 81(3):1179–1189

    Article  MATH  Google Scholar 

  25. Zhou W, Yang J, Yang X (2014) Almost surely exponential stability of neural networks with Lévy noise and Markovian switching. Neurocomputing 145:154–159

    Article  Google Scholar 

  26. Caraballo T, Garrido-Atienza MJ, Taniguchi T (2011) The existence and exponential behavior of solutions to stochastic delay evolution equations with a fractional Brownian motion. Nonlinear Anal 74:3671–3684

    Article  MathSciNet  MATH  Google Scholar 

  27. Diop MA, Garrido-Atienza MJ (2014) Retarded evolution systems driven by fractional Brownian motion with Hurst parameter \(H>\frac{1}{2}\). Nonlinear Anal Theory Methods Appl 97:15–29

    Article  MathSciNet  MATH  Google Scholar 

  28. Duncan TE, Maslowski B, Pasik-Duncan B (2005) Stochastic equations in Hilbert space with a multiplicative fractional Gaussian noise. Stoch Process Their Appl 115:1357–1383

    Article  MathSciNet  MATH  Google Scholar 

  29. Boufoussi B, Hajji S (2012) Neutral stochastic functional differential equations driven by a fractional Brownian motion in a Hilbert space. Stat Probab Lett 82:1549–1558

    Article  MathSciNet  MATH  Google Scholar 

  30. Ke Y, Miao C (2015) Stability analysis of fractional-order Cohen–Grossberg neural networks with time delay. Int J Comput Math 92(6):1102–1113

    Article  MathSciNet  MATH  Google Scholar 

  31. Zhang S, Yu Y, Wang H (2015) Mittag–Leffler stability of fractional-order Hopfield neural networks. Nonlinear Anal Hybrid Syst 16:104–121

    Article  MathSciNet  MATH  Google Scholar 

  32. Wang H, Yu Y, Wen G (2015) Global stability analysis of fractional-order Hopfield neural networks with time delay. Neurocomputing 154:15–23

    Article  Google Scholar 

  33. Bao H, Cao J (2015) Projective synchronization of fractional-order memristor-based neural networks. Neural Netw 63:1–9

    Article  MATH  Google Scholar 

  34. Rakkiyappan R, Cao J, Velmurugan G (2015) Existence and uniform stability analysis of fractional-order complex-valued neural networks with time delays. IEEE Trans Neural Netw Learn Syst 26(1):84–97

    Article  MathSciNet  MATH  Google Scholar 

  35. Mishura Y (2008) Stochastic calculus for fractional Brownian motion and related processes. In: Lecture notes in mathematics, Springer, Heidelberg

    Google Scholar 

  36. Yu W, Cao J (2007) Synchronization control of stochastic delayed neural networks. Phys A 373:252–260

    Article  Google Scholar 

  37. Su S, Lin Z, Garcia A (2016) Distributed synchronization control of multiagent systems with unknown nonlinearities. IEEE Trans Cybern 46(1):325–338

    Article  Google Scholar 

Download references

Acknowledgments

This work is partially supported by the Open Research Fund Program of Institute of Applied Mathematics Yangtze University (Grant No. KF1602).

Author information

Authors and Affiliations

  1. School of Information and Mathematics, Yangtze University, Jingzhou, 434023, China

    Xianghui Zhou & Zhi Li

  2. School of Mathematics and Statistics, Anyang Normal University, Anyang, 455000, China

    Jun Yang

  3. College of Electronic and Electrical Engineering, Shanghai University of Engineering Science, Shanghai, 201620, China

    Dongbing Tong

Authors
  1. Xianghui Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jun Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zhi Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Dongbing Tong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xianghui Zhou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, X., Yang, J., Li, Z. et al. pth Moment synchronization of Markov switched neural networks driven by fractional Brownian noise. Neural Comput & Applic 29, 823–836 (2018). https://doi.org/10.1007/s00521-016-2593-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-016-2593-0

Keywords