Skip to main content
Springer Nature Link
Log in

Analytical scrutiny of nonlinear equation of hypocycloid motion by AGM

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

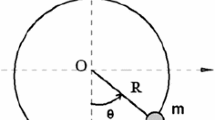
The curve produced by fixed point on the circumference of a small circle of specified radius rolling around the inside of a large circle with bigger radius than the other one is named hypocycloid. In the present paper, a semi-hypocycloid motion of a cylinder has been simulated by extracting the governing nonlinear differential equation of this especial motion, and then, the obtained equation has been solved completely by a simple and innovative approach which we have named it Akbari–Ganji’s method (AGM). On the basis of comparisons which have been made between the gained solutions by AGM, numerical method (Runge–Kutta 4th) and VIM, it is possible to indicate that AGM can be successfully applied for various differential equations. In this paper, a nonlinear vibrational equation has been solved by AGM, and afterward, the application of AGM will be shown in our own specified problem. It is noteworthy that this method has some valuable advantages, for instance in this approach, it is not necessary to utilize dimensionless parameters in order to simplify equation. So there is no need to convert the variables to new ones that heightens the complexity of the problem. Moreover by utilizing AGM, the shortage of boundary condition(s) for solving differential equation will be terminated by using derivatives of main differential equation(s). The results reveal that this method is very effective, simple, reliable and can be applied for many other nonlinear problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Abbreviations

u(t):

Vibrational displacement \(\left( {\text{m}} \right)\)

\(\dot{u}(t)\) :

Vibrational velocity \(\left( {\frac{\text{m}}{\text{s}}} \right)\)

\({\ddot{u}}(t)\) :

Vibrational acceleration \(\left( {\frac{\text{m}}{{{\text{s}}^{2} }}} \right)\)

\(\theta \left( t \right)\) :

Angular position as a function of time \(\left( {\text{rad}} \right)\)

\(A\) :

Initial amplitude of vibration \(\left( {\text{m}} \right)\)

\(\omega\) :

Angular frequency \(\left( {\frac{\text{rad}}{\text{s}}} \right)\)

\(\ddot{\psi }(t)\) :

Angular acceleration \(\left( {\frac{\text{rad}}{{{\text{s}}^{2} }}} \right)\)

\(g\) :

Gravity acceleration \(\left( {\frac{\text{m}}{{{\text{s}}^{2} }}} \right)\)

\(m\) :

Mass of the cylinder \(\left( {\text{kg}} \right)\)

\(w\) :

Weight of the cylinder \(\left( {\text{N}} \right)\)

\(I_{\text{c}}\) :

Mass moment of inertia about instantaneous center \(\left( {{\text{kg}}\,{\text{m}}^{2} } \right)\)

\(\sum {M_{\text{c}} }\) :

Resultant moment about instantaneous center of rotation \(\left( {{\text{N}}\,{\text{m}}} \right)\)

\(R\) :

Radius of circular path \(\left( {\text{m}} \right)\)

\(r\) :

Radius of the cylinder \(\left( {\text{m}} \right)\)

References

  1. Sheikholeslami M, Sheykholeslami FB, Khoshhal S (2014) Effect of magnetic field on Cu-water nanofluid heat transfer using GMDH-type neural network. Neural Comput Appl 25:171–178

    Article  Google Scholar 

  2. Sheikholeslami M, Ganji DD, Ashorynejad HR (2012) Analytical investigation of Jeffery-Hamel flow with high magnetic field and nanoparticle by Adomian decomposition method. Appl Math Mech 33:25–36

    Article  MathSciNet  MATH  Google Scholar 

  3. Imani AA, Ganji DD, Rokni HB, Latifizadeh H (2012) Approximate traveling wave solution for shallow water wave equation. Appl Math Model 36:1550–1557

    Article  MathSciNet  MATH  Google Scholar 

  4. Sfahani MG, Barari A, Omidvar M, Ganji SS, Domairry G (2011) Dynamic response of inextensible beams by improved energy balance method. Proc Inst Mech Eng Part K J Multi-body Dyn 225(1):66–73

    Google Scholar 

  5. Sheikholeslami M, Ashorynejad HR, Domairry G, Hashim I (2012) Flow and heat transfer of Cu-water nanofluid between a stretching sheet and a porous surface in a rotating system. Journal of Applied Mathematics 2012(2012). doi:10.1155/2012/421320

  6. He JH (1999) Variational iteration method: a kind of nonlinear analytical technique: some examples. Int J Non-Linear Mech 344:699

    Article  MATH  Google Scholar 

  7. Ganji SS, Ganji DD, Babazadeh H, Sadoughi N (2010) Application of amplitude-frequency formulation to nonlinear oscillation system of the motion of a rigid rod rocking back. Math Methods Appl Sci 33(2):157–166

    MathSciNet  MATH  Google Scholar 

  8. He Ji-Huan, Xu-Hong Wu (2006) Exp-function method for nonlinear wave equations. Chaos Solitos Fractals 30(3):700–708

    Article  MathSciNet  MATH  Google Scholar 

  9. Chang JR (2011) The exp-function method and generalized solitary solutions. Comput Math Appl 61(8):2081–2084

    Article  MathSciNet  MATH  Google Scholar 

  10. Ganji ZZ, Ganji DD, Bararnia H (2009) Approximate general and explicit solutions of nonlinear BBMB equations exp-function method. Appl Math Model 33(4):1836–1841

    Article  MathSciNet  MATH  Google Scholar 

  11. Ahmadi AR, Zahmatkesh A, Hatami M, Ganj DD (2014) A comprehensive analysis of the flow and heat transfer for a nanofluid over an unsteady stretching flat plate. Powder Technol 258:125–133

    Article  Google Scholar 

  12. Mirzaee Farshid (2011) Differential transform method for solving linear and nonlinear systems of ordinary differential equations. Appl Math Sci 5(70):3465–3472

    MathSciNet  MATH  Google Scholar 

  13. Jafari H, Alipour M, Tajadodi H (2010) Two-dimensional differential transform method for solving nonlinear partial differential equation. Int J Res Rev Appl Sci 2:47–52

    MATH  Google Scholar 

  14. Sheikholeslami M, Ashorynejad HR, Ganji DD, Kolahdooz A (2011) Investigation of rotating MHD viscous flow and heat transfer between stretching and porous surfaces using analytical method. Math Probl Eng 2011(2011). doi:10.1155/2011/258734

  15. He JH (2004) The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl Math Comput 151:287–292

    MathSciNet  MATH  Google Scholar 

  16. Sheikholeslamia M, Ganjia DD, Ashorynejad HR (2013) Investigation of squeezing unsteady nanofluid flow using ADM. Powder Technol 239:259–265

    Article  Google Scholar 

  17. Akbari MR, Ganji DD, Majidian A, Ahmadi AR (2014) Solving nonlinear differential equations of Vanderpol, Rayleigh and Duffing by AGM. Research Article, Higher Education Press and Springer, Berlin, 9(2):177–190

  18. Meresht NB, Ganji DD (2016) Solving nonlinear differential equation arising in dynamical systems by AGM. Int J Appl Comput Math. doi:10.1007/s40819-015-0131-x-2016

    Google Scholar 

  19. Meriam JL, Kraige LG (2012) Engineering mechanics dynamics, 7th edn. Wiley, Hoboken

    MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to Alireza Ahmadi, who helped to improve and amend the paper with his useful and practical suggestions.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Babol Noshirvani University of Technology, P.O. Box 484, Babol, Iran

    Navid Balazadeh Meresht & D. D. Ganji

Authors
  1. Navid Balazadeh Meresht
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. D. D. Ganji
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Navid Balazadeh Meresht.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Meresht, N.B., Ganji, D.D. Analytical scrutiny of nonlinear equation of hypocycloid motion by AGM. Neural Comput & Applic 29, 1575–1582 (2018). https://doi.org/10.1007/s00521-016-2654-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-016-2654-4

Keywords