Skip to main content
Springer Nature Link
Log in

A mathematical model of MHD nanofluid flow having gyrotactic microorganisms with thermal radiation and chemical reaction effects

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

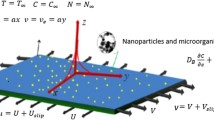
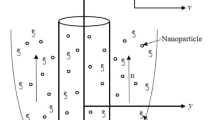
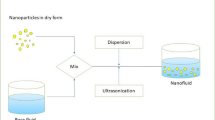
In this article, we have examined three-dimensional unsteady MHD boundary layer flow of viscous nanofluid having gyrotactic microorganisms through a stretching porous cylinder. Simultaneous effects of nonlinear thermal radiation and chemical reaction are taken into account. Moreover, the effects of velocity slip and thermal slip are also considered. The governing flow problem is modelled by means of similarity transformation variables with their relevant boundary conditions. The obtained reduced highly nonlinear coupled ordinary differential equations are solved numerically by means of nonlinear shooting technique. The effects of all the governing parameters are discussed for velocity profile, temperature profile, nanoparticle concentration profile and motile microorganisms’ density function presented with the help of tables and graphs. The numerical comparison is also presented with the existing published results as a special case of our study. It is found that velocity of the fluid diminishes for large values of magnetic parameter and porosity parameter. Radiation effects show an increment in the temperature profile, whereas thermal slip parameter shows converse effect. Furthermore, it is also observed that chemical reaction parameter significantly enhances the nanoparticle concentration profile. The present study is also applicable in bio-nano-polymer process and in different industrial process.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Abbreviations

\(\bar{u},\bar{v},\bar{w}\) :

Velocity components

\(\bar{r},\bar{z}\) :

Cylindrical coordinate

Re :

Reynolds number

\(\tilde{t}\) :

Time

\(\bar{C}\) :

Nanoparticle volume fraction

\(\bar{P}\) :

Pressure

F w :

Suction/injection parameter

\(\bar{T}_{\infty }\) :

Atmosphere temperature

\(\bar{C}_{\infty }\) :

Atmosphere concentration

\(\bar{T}_{w}\) :

Surface temperature

N t :

Thermophoresis parameter

N b :

Brownian motion parameter

N 1 :

Velocity slip parameter

\(\bar{n}_{w}\) :

Surface density of motile-organism

\(\bar{k}_{\text{p}}\) :

Permeability of porous medium

\(\bar{t}\) :

Time

J :

Heat flux of microorganisms

a 0 (>0):

Constant

c F :

Forchheimer coefficient

Q 0 :

Heat source/sink

\(\bar{D}_{1}\) :

Thermal slip factor

\(D_{{\bar{T}}}\) :

Thermophoretic diffusion coefficient

\(\bar{n}\) :

Density of motile microorganisms

\(\bar{b}\) :

Chemotaxis constant

W c :

Maximum cell swimming speed

S :

Unsteady parameter

D B :

Brownian diffusion coefficient

\(D_{{\bar{n}}}\) :

A micro-organism diffusivity

Pr :

Prandtl number

Sc :

Schmidt number

Sb :

Bio-convection Schmidt number

Pe :

Peclet number

k f :

Forchheimer number

M :

Magnetic parameter

R d :

Thermal radiation parameter

H S :

Heat source/sink parameter

q w :

Surface heat flux

q M :

Surface mass flux

q N :

Motile surface microorganism flux

k′:

Mean absorption coefficient

\(C_{{F\bar{x}}}\) :

Skin friction coefficient

\(Nu_{{\bar{x}}}\) :

Nusselt number

\(Sh_{{\bar{x}}}\) :

Sherwood number

\(N_{{n\bar{x}}}\) :

Density number of motile microorganisms

\(\bar{\beta }\) :

Contraction expansion strength

\(\bar{\alpha }_{m}\) :

Thermal conductivity

(ρc)f :

Heat capacity of the fluid

(ρc)p :

Heat capacity of nanoparticle

σ :

Electrical conductivity

μ :

Viscosity of nanofluid

θ :

Temperature profile

ϕ :

Nanoparticle concentration profile

Φ:

Motile microorganism density profile

\(\bar{\sigma }\) :

Stefan–Boltzmann constant

β :

Velocity slip

τ w :

Shear stress

ρ p :

Density of nanoparticles

σ :

Electrical conductivity

β T :

Thermal slip

ρ :

Density

ν :

Kinematic viscosity

γ :

Chemical reaction parameter

References

  1. Thomas S, Yang W (eds) (2009) Advances in polymer processing: from macro-to nano-scales. Woodhead Publishing, Oxford

    Google Scholar 

  2. Bachok N, Ishak A (2010) Flow and heat transfer over a stretching cylinder with prescribed surface heat flux. Malays J Math Sci 4:159–169

    MATH  Google Scholar 

  3. Stasiak J, Squires AM, Castelletto V, Hamley IW, Moggridge GD (2009) Effect of stretching on the structure of cylinder and sphere-forming styrene–isoprene–styrene block copolymers. Macromolecules 42:5256–5265

    Article  Google Scholar 

  4. Sakiadis BC (1961) Boundary layer behaviour on continuous solid surfaces: I. Boundary layer equations for two-dimensional and axisymmetric flow. AIChE J 7:26–28

    Article  Google Scholar 

  5. Crane LJ (1970) Flow past a stretching plate. Z Angew Math Phys 21(4):645–647. doi:10.1007/BF01587695

    Article  Google Scholar 

  6. Datta BK, Roy P, Gupta AS (1985) Temperature field over a stretching sheet with uniform heat flux. Int J Heat Mass Trans 12:89–94

    Article  Google Scholar 

  7. Chen CK, Char MI (1988) Heat transfer of a continuous stretching surface with suction and blowing. J Math Anal Appl 135:568–580

    Article  MathSciNet  MATH  Google Scholar 

  8. Bhatti MM, Shahid A, Rashidi MM (2016) Numerical simulation of fluid flow over a shrinking porous sheet by successive linearization method. Alex Eng J 55:51–56

    Article  Google Scholar 

  9. Bhatti MM, Abbas T, Rashidi MM (2016) A New numerical simulation of MHD stagnation-point flow over a permeable stretching/shrinking sheet in porous media with heat transfer. Iran J Sci Technol Trans A Sci. doi:10.1007/s40995-016-0027-6

    Google Scholar 

  10. Saidur R, Leong KY, Mohammad HA (2011) A review on applications and challenges of nanofluids. Renew sustain Energy Rev 15:1646–1668

    Article  Google Scholar 

  11. Wong KV, De Leon O (2010) Applications of nanofluids: current and future. Adv Mech Eng 2:519659

    Article  Google Scholar 

  12. Yu W, Xie H (2012) A review on nanofluids: preparation, stability mechanisms, and applications. J Nanomater 2012:1

    Google Scholar 

  13. Raees A, Xu H, Liao SJ (2015) Unsteady mixed nano-bioconvection flow in a horizontal channel with its upper plate expanding or contracting. Int J Heat Mass Transf 86:174–182

    Article  Google Scholar 

  14. Anoop KB, Sundararajan T, Das SK (2009) Effect of particle size on the convective heat transfer in nanofluid in the developing region. Int J Heat Mass Transf 52:2189–2195

    Article  MATH  Google Scholar 

  15. Pedley TJ (2010) Instability of uniform micro-organism suspensions revisited. J Fluid Mech 647:335–359

    Article  MathSciNet  MATH  Google Scholar 

  16. Xu H, Pop I (2014) Mixed convection flow of a nanofluid over a stretching surface with uniform free stream in the presence of both nanoparticles and gyrotactic microorganisms. Int J Heat Mass Transf 75:610–623

    Article  Google Scholar 

  17. Aziz A, Khan WA, Pop I (2012) Free convection boundary layer flow past a horizontal flat plate embedded in porous medium filled by nanofluid containing gyrotactic microorganisms. Int J Therm Sci 56:48–57

    Article  Google Scholar 

  18. Tham L, Nazar R, Pop I (2013) Mixed convection flow over a solid sphere embedded in a porous medium filled by a nanofluid containing gyrotactic microorganisms. Int J Heat Mass Transf 62:647–660

    Article  Google Scholar 

  19. Saranya S, Radha KV (2014) Review of nanobiopolymers for controlled drug delivery. Polym Plast Technol Eng 53:1636–1646

    Article  Google Scholar 

  20. Oh JK, Lee DI, Park JM (2009) Biopolymer-based microgels/nanogels for drug delivery applications. Prog Polym Sci 34:1261–1282

    Article  Google Scholar 

  21. Abo-Eldahab EM, Abd El-Aziz M (2000) Radiation effect on heat transfer in electrically conducting fluid at a stretching surface with uniform free stream. J Phys D Appl Phys 33:3180–3185

    Article  Google Scholar 

  22. Cortell R (2008) Effects of viscous dissipation and radiation on the thermal boundary layer over a nonlinearly stretching sheet. Phys Lett A 372:631–636

    Article  MATH  Google Scholar 

  23. Cortell R (2006) Effects of viscous dissipation and work done by deformation on MHD flow and heat transfer of a viscoelastic fluid over a stretching sheet. Phys Lett A 357:298–305

    Article  MATH  Google Scholar 

  24. Bhatti MM, Abbas T, Rashidi MM, Ali MES (2016) Numerical simulation of entropy generation with thermal radiation on MHD carreau nanofluid towards a shrinking sheet. Entropy 18(6):200

    Article  MathSciNet  Google Scholar 

  25. Bhatti MM, Rashidi MM (2016) Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J Mol Liq 221:567–573

    Article  Google Scholar 

  26. Bhatti MM, Rashidi MM (2016) Entropy generation with nonlinear thermal radiation in MHD boundary layer flow over a permeable shrinking/stretching sheet: numerical solution. J Nanofluids 5:543–548

    Article  Google Scholar 

  27. Anjalidevi SP, Kandasamy R (1999) Effects of chemical reaction, heat and mass transfer on laminar flow along a semi infinite horizontal plate. Heat Mass Transf 35:465–467

    Article  Google Scholar 

  28. Hayat T, Muhammad T, Shehzad AS, Alsaedi A (2015) Similarity solution to threedimensional boundary layer flow of second grade nanofluid past a stretching surface with thermal radiation and heat source/sink. AIP Adv 5:017107

    Article  Google Scholar 

  29. Abel MS, Siddheshwar PG, Mahesha N (2009) Effects of thermal buoyancy and variable thermal conductivity on the MHD flow and heat transfer in a power-law fluid past a vertical stretching sheet in the presence of a non-uniform heat source. Int J Non Linear Mech 44:1–12

    Article  MATH  Google Scholar 

  30. Sheikholeslami M, Rashidi MM (2015) Effect of space dependent magnetic field on free convection of Fe3O4–water nanofluid. J Taiwan Inst Chem Eng. doi:10.1016/jjtice.2015.03.035

    Google Scholar 

  31. Sheikholeslami M (2014) Effect of spatially variable magnetic field on ferrofluid flow and heat transfer considering constant heat flux boundary condition. Eur Phys J Plus 2014:129–248

    Google Scholar 

  32. Sheikholeslami M, Ganji DD, Rashidi MM (2015) Ferrofluid flow and heat transfer in a semi annulus enclosure in the presence of magnetic source considering thermal radiation. J Taiwan Inst Chem Eng 47:6–17

    Article  Google Scholar 

  33. Ishak A, Nazar R, Pop I (2008) Magnetohydrodynamics flow and heat transfer due to a stretching cylinder. Energy Convers Manag 49:3265–3269

    Article  MATH  Google Scholar 

  34. Mukhopadhyay S (2013) MHD boundary layer slip flow along a stretching cylinder. Ain Shams Eng J 4:317–324

    Article  Google Scholar 

  35. Ishak A (2010) Unsteady MHD flow and heat transfer over a stretching plate. J Appl Sci 10:2127–2131

    Article  Google Scholar 

  36. Pop I, Na TY (1998) A note on MHD flow over a stretching permeable surface. Mech Res Commun 25:263–269

    Article  MathSciNet  MATH  Google Scholar 

  37. Khan K, Abel MS, Sonth RM (2003) Visco-elastic MHD flow heat and mass transfer over a porous stretching sheet with dissipation of energy and stress work. Heat Mass Trans 40:47–57

    Article  Google Scholar 

  38. Abed Mahdi R, Mohammed HA, Munisamy KM, Saeid NH (2015) Review of convection heat transfer and fluid flow in porous media with nanofluid. Renew Sust Energy Rev 41:715–734

    Article  Google Scholar 

  39. Abed Mahdi R, Mohammed HA, Munisamy KM (2013) Improvement of convection heat transfer by using porous media and nanofluid: review. Int J Sci Res 2:34–47

    Google Scholar 

  40. Das KS, Choi SU, Yu W, Pradep T (2007) Nanofluid: science and technology. Wiley, London

    Book  Google Scholar 

  41. James M, Mureithi EW, Kuznetsov D (2014) Natural convection flow past an impermeable vertical plate embedded in nanofluid saturated porous medium with temperature dependent viscosity. Asian J Math Appl 2014:ama0165

    Google Scholar 

  42. Ishak A, Nazar R, Pop I (2008) Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Energy Convers Manag 49:3265–3269

    Article  MATH  Google Scholar 

  43. Wang CY (1988) Fluid flow due to a stretching cylinder. Phys Fluids 31:466–468

    Article  Google Scholar 

  44. Basir MFM, Uddin MJ, Ismail AM, Bég OA (2016) Nanofluid slip flow over a stretching cylinder with Schmidt and Péclet number effects. AIP Adv 6:055316

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai, 200072, China

    M. M. Bhatti

  2. Department of Mathematics, Siksha ‘O’ Anusandhan University, Khandagiri, Bhubaneswar, Odisha, 751030, India

    S. R. Mishra

  3. Department of Mathematics, Quaid-I-Azam University, Islamabad, 44000, Pakistan

    T. Abbas

  4. Shanghai Key Lab of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Tongji University, Shanghai, 201804, China

    M. M. Rashidi

Authors
  1. M. M. Bhatti
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. R. Mishra
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. T. Abbas
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. M. M. Rashidi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to M. M. Bhatti.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bhatti, M.M., Mishra, S.R., Abbas, T. et al. A mathematical model of MHD nanofluid flow having gyrotactic microorganisms with thermal radiation and chemical reaction effects. Neural Comput & Applic 30, 1237–1249 (2018). https://doi.org/10.1007/s00521-016-2768-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-016-2768-8

Keywords