Abstract
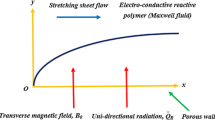
This article presents an analysis of stagnation point of coupled flow and heat transfer of an upper-convected Maxwell fluid over a stretching sheet along with magnetic effects and slip condition at the boundary. The recently proposed Cattaneo–Christov model is employed in the energy equation to investigate the effects of thermal relaxation time. Similarity transformations are adopted to convert the governing partial differential equations into ordinary differential equations. Numerical solution of the system of ODEs is achieved by shooting method together with Runge–Kutta method of order four. The effects of stretching ratio parameter (0 ≤ e ≤ 0.5), elasticity number (0 ≤ β ≤ 1.5), heat flux relaxation time (0 ≤ γ ≤ 1.5), magnetic parameter (0 ≤ M ≤ 1.5), slip coefficient (1 ≤ b ≤ 4) and Prandtl number (0 ≤ Pr ≤ 1.5) on velocity and temperature are investigated graphically and numerically. It is observed that temperature boosts up with an increase in thermal relaxation time.












Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Abbreviations
- a, c :
-
Constants (1/time)
- b :
-
Slip coefficient
- e :
-
Stretching ratio parameter \( \left( {\tfrac{c}{a}} \right) \)
- T w :
-
Wall temperature (K)
- f′:
-
Dimensionless velocity \( \left( {\tfrac{\text{m}}{\text{s}}} \right) \)
- M :
-
Magnetic parameter
- \( {\mathbf{V}} \) :
-
Velocity vector \( \left( {\tfrac{\text{m}}{\text{s}}} \right) \)
- Pr:
-
Prandtl number \( \left( {\tfrac{\nu }{\alpha }} \right) \)
- α :
-
Thermal diffusivity \( \left( {\tfrac{{{\text{m}}^{ 2} }}{\text{s}}} \right) \)
- η :
-
Similarity variable (m)
- σ :
-
Electrical conductivity \( \left( {\tfrac{\text{S}}{\text{m}}} \right) \)
- λ 1 :
-
Relaxation time of the fluid (s)
- σ v :
-
Tangential momentum accommodation
- θ :
-
Dimensionless temperature (K)
- B 0 :
-
Magnetic field strength (T)
- c p :
-
Specific heat \( \left( {\tfrac{\text{J}}{\text{kgK}}} \right) \)
- T :
-
Temperature of fluid (K)
- T ∞ :
-
Ambient temperature (K)
- (x, y):
-
Coordinate axis (m)
- k :
-
Thermal conductivity \( \left( {\tfrac{\text{W}}{\text{mK}}} \right) \)
- \( {\mathbf{q}} \) :
-
Heat flux \( \left( {\tfrac{\text{J}}{\text{s}}} \right) \)
- (u, v):
-
Velocity components \( \left( {\tfrac{\text{m}}{\text{s}}} \right) \)
- β :
-
Elasticity number
- ρ :
-
Density of fluid \( \left( {\tfrac{\text{kg}}{{{\text{m}}^{ 3} }}} \right) \)
- λ 0 :
-
Free path of molecular mean
- λ 2 :
-
Relaxation time of heat flux (s)
- ν :
-
Kinematic viscosity \( \left( {\tfrac{{{\text{m}}^{ 2} }}{\text{s}}} \right) \)
- γ :
-
Thermal relaxation time (s)
References
Rashidi MM, Erfani E (2012) Analytical method for solving steady MHD convective and slip flow due to a rotating disk with viscous dissipation and ohmic heating. Eng Comput 29:562–579
Ab olbashari MH, Freido onimehr N, Nazari F, Rashidi MM (2014) Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technol 267:256–267
Rashidi MM, Ali M, Freidoonimehr N, Rostami B, Hossain MA (2014) Mixed convective heat transfer for MHD viscoelastic fluid flow over a porous wedge with thermal radiation. Mech Eng Adv. doi:10.1155/2014/735939
Freidoonimehr N, Rashidi MM, Mahmud S (2015) Unsteady MHD free convective flow past a permeable stretching vertical surface in a nano-fluid. Int J Ther Sci 87:136–145
Turkyilmazoglu M (2016) Magnetic field and slip effects on the flow and heat transfer of stagnation point Jeffrey fluid over deformable surfaces. Int J Heat Mass Transf 71:549–556
Turkyilmazoglu M (2015) An analytical treatment for the exact solutions of MHD flow and heat over two-three dimensional deforming bodies. Int J Heat Mass Transf 90:781–789
Turkyilmazoglu M (2012) Multiple analytic solutions of heat and mass transfer of magnetohydrodynamic slip flow for two types of viscoelastic fluids over a stretching surface. J Heat Transf 134:071701–1–071701–9
Turkyilmazoglu M (2016) Equivalences and correspondences between the deforming body induced flow and heat in two-three dimensions. Phys Fluids 28:043102–1–043102–10
Cattaneo C (1948) Sulla conduzione del calore. Atti Semin Mat Fis Univ Modena Reggio Emilia 3:83–101
Christov CI (2009) On frame indifferent formulation of the Maxwell–Cattaneo model of finite speed heat conduction. Mech Res Commun 36:481–486
Straughan B (2010) Thermal convection with the Cattaneo–Christov model. Int J Heat Mass Transf 53:95–98
Tibullo V, Zampoli V (2011) A uniqueness result for the Cattaneo–Christov heat conduction model applied to incompressible fluids. Mech Res Commun 38:77–99
Han S, Zheng L, Li C, Zhang X (2014) Coupled flow and heat transfer in viscoelastic fluid with Cattaneo–Christov heat flux model. Appl Math Lett 38:87–93
Khan JA, Mustafa M, Hayat T, Alsaedi A (2015) Numerical study of Cattaneo–Christov heat flux model for viscoelastic flow due to an exponentially stretching surface. PLoS ONE 10(9):e0137363
Hie menz K (1911) Die Grenzschicht an einem in den gleichfrmigen flessigkeitsstrom eingetauchten geraden Kreiszylinder. Ding Polytech J 5:321–326
Homann F (1936) Die einfluss grsse zahigkeit bei der strmung um der zylinder und um die kugel. J Appl Math Mech 16:153–164
Choi JJ, Rusak Z, Tichy JA (1999) Maxwell fluid suction flow in a channel. Non-Newtonian Fluid Mech 85:165–187
Abbas Z, Sajid M, Hayat T (2006) MHD boundary-layer flow of an upper-convected Maxwell fluid in a porous channel. Theor Comput Fluid Dyn 20:229–238
Aliakbar V, Pahlavan AA, Sadeghy K (2009) The influence of thermal radiation on MHD flow of Maxwellian fluids above stretching sheets. Commun Nonlinear Sci Numer Simul 14:779–794
Mustafa M (2015) Cattaneo–Christov heat flux model for rotating flow and heat transfer of upper convected Maxwell fluid. AIP Adv 5:047109
Kumaria M, Nath G (2009) Steady mixed convection stagnation-point flow of upper convected Maxwell fluids with magnetic field. Int J Non-Linear Mech 44:1048–1055
Sadeghy K, Hajibeygib H, Taghavia SM (2006) Stagnation-point flow of upper-convected Maxwell fluids. Int J Non-Linear Mech 41:1242–1247
Hayat T, Awais M, Qasim M, Hendi AA (2011) Effects of mass transfer on the stagnation point flow of an upper-convected Maxwell (UCM) fluid. Int J Heat Mass Transf 54:3777–3782
Hayat T, Mustafa M, Shehzad SA, Obaidat S (2012) Melting heat transfer in the stagnation-point flow of an upper-convected Maxwell (UCM) fluid past a stretching sheet. Int J Numer Meth Fluids 68:233–243
Hayat T, Khan MI, Farooq M, Yasmeen T, Alsaedi A (2016) Stagnation point flow with Cattaneo–Christov heat flux and homogeneous-heterogeneous reactions. J Mol Liq 220:49–55
Sui J, Zheng L, Zhang X (2016) Boundary layer heat and mass transfer with Cattaneo Christov double-diffusion in upper-convected Maxwell fluid past a stretching sheet with slip velocity. Int J Ther Sci 104:461468
Na TY (1979) Computational methods in engineering boundary value problems. Academic Press, London
Abel MS, Tawade JV, Nandeppanavar MM (2012) MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica 47:385393
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Authors have no conflict of interest for this publication.
Rights and permissions
About this article
Cite this article
Mehmood, Y., Sagheer, M., Hussain, S. et al. MHD stagnation point flow and heat transfer in viscoelastic fluid with Cattaneo–Christov heat flux model. Neural Comput & Applic 30, 2979–2986 (2018). https://doi.org/10.1007/s00521-017-2902-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-017-2902-2