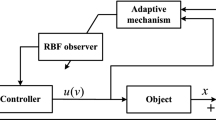
Abstract
This paper focuses on the state-feedback control problem for a class of high-order nonlinear systems with unknown time delay and control coefficients. Based on a novel dynamic gain-based backstepping technique and radial basis function neural network (RBF NN) approximation approach, the restrictions on high-order and nonlinearities are removed or further relaxed. Under these weaker conditions, a smooth state-feedback controller is skillfully constructed with only one adaptive parameter. In addition, the knowledge of time delay, NN nodes and weights is not necessary to be known a priori. It is proven that the designed controller can render the closed-loop system be semi-globally uniformly ultimately bounded. Finally, both practical and numerical examples are shown to demonstrate the effectiveness of the proposed scheme.


Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Khalil HK (2002) Nonlinear systems, 3rd edn. Prentice-Hall, New York
Isidori A (1995) Nonlinear control systems, 3rd edn. Springer, London
Ge SS, Hong F, Lee TH (2005) Robust adaptive control of nonlinear systems with unknown time delays. Automatica 41(7):1181–1190
Zhang X, Baron L, Liu Q, Boukas EK (2011) Design of stabilizing controllers with a dynamic gain for feedforward nonlinear time-delay systems. IEEE Trans Autom Control 56(3):692–697
Jo HW, Choi HL, Lim JT (2014) Observer based output feedback regulation of a class of feedforward nonlinear systems with uncertain input and state delays using adaptive gain. Syst Control Lett 71:44–53
Zhang Z, Xu S (2015) Observer design for uncertain nonlinear systems with unmodeled dynamics. Automatica 51:80–84
Wang Z, Zhai J, Ai W, Fei S (2015) Global practical tracking for a class of uncertain nonlinear systems via sampled-data control. Appl Math Comput 260:257–268
Shen Q, Shi P (2015) Distributed command filtered backstepping consensus tracking control of nonlinear multiple-agent systems in strict-feedback form. Automatica 53(3):120–124
Wu Z, Cui M, Shi P (2012) Backstepping control in vector form for stochastic Hamiltonian systems. SIAM J Control Optim 50(2):925–942
Nguang SK (2000) Robust stabilization of a class of time-delay nonlinear systems. IEEE Trans Autom Control 45(4):756–762
Lin W, Qian C (2000) Adding one power integrator: a tool for global stabilization of high-order lower-triangular systems. Syst Control Lett 39(4):339–351
Lin W, Qian C (2000) Adaptive regulation of high-order lower-triangular systems: adding a power integrator technique. Syst Control Lett 39(5):353–364
Sun ZY, Xue LY, Zhang K (2015) A new approach to finite-time adaptive stabilization of high-order uncertain nonlinear system. Automatica 58:60–66
Zhang J, Liu YG (2011) A new approach to adaptive control design without over-parametrization for a class of uncertain nonlinear systems. Sci China Inf Sci 54(7):1419–1429
Zhang XH, Xie XJ (2014) Global state feedback stabilisation of nonlinear systems with high-order and low-order nonlinearities. Int J Control 87(3):642–652
Qian C (2005) A homogeneous domination approach for global output feedback stabilization of a class of nonlinear systems. In: Proceedings of the American control conference, Portland USA, pp 4708–4715
Xie XJ, Duan N, Yu X (2011) State-feedback control of high-order stochastic nonlinear systems with SiISS inverse dynamics. IEEE Trans Autom Control 56(8):1921–1926
Xie XJ, Duan N, Zhao CR (2014) A combined homogeneous domination and sign function approach to output-feedback stabilization of stochastic high-order nonlinear systems. IEEE Trans Autom Control 56(5):1303–1309
Xie XJ, Duan N (2010) Output tracking of high-order stochastic nonlinear systems with application to benchmark mechanical system. IEEE Trans Autom Control 55(5):1197–1202
Qian C, Lin W (2006) Recursive observer design, homogeneous approximation and nonsmooth output feedback stabilization of nonlinear systems. IEEE Trans Autom Control 51(9):1457–1471
Zhou S, Feng G, Nguang SK (2002) Comments on ‘Robust stabilization of a class of time-delay nonlinear systems’. IEEE Trans Autom Control 47(9):1586–1586
Li G, Zang C, Liu X (2003) Comments on ‘Robust stabilization of a class of time-delay nonlinear systems’. IEEE Trans Autom Control 48(5):908–908
Lv LN, Sun ZY, Xie XJ (2015) Adaptive control for high-order time-delay uncertain nonlinear system and application to chemical reactor system. Int J Adapt Control Signal Process 29:224–241
Gao F, Wu Y (2015) Further results on global state feedback stabilization of high-order nonlinear systems with time-varying delays. ISA Trans 55:41–48
Sun ZY, Zhang XH, Xie XJ (2013) Continuous global stabilisation of high-order time-delay nonlinear systems. Int J Control 86(6):994–1007
Sun ZY, Liu ZG, Zhang XH (2015) New results on global stabilization for time-delay nonlinear systems with low-order and high-order growth conditions. Int J Robust Nonlinear Control 25(6):878–899
Zhang X, Lin Y (2014) Global stabilization of high-order nonlinear time-delay systems by state feedback. Syst Control Lett 65:89–95
Zhang X, Lin Y (2015) Adaptive control of nonlinear time-delay systems with application to a two-stage chemical reactor. IEEE Trans Autom Control 60(4):1074–1079
Zhang X, Lin W, Lin Y (2017) Nonsmooth feedback control of time-delay nonlinear systems: a dynamic gain based approach. IEEE Trans Autom Control 62(1):438–444
Manivannan R, Mahendrakumar G, Samidurai R, Cao J, Alsaedi A (2017) Exponential stability and extended dissipativity criteria for generalized neural networks with interval time-varying delay signals. J Franklin Inst 354(11):4353–4376
Zhong J, Lu J, Liu Y, Cao J (2014) Synchronization in an array of output-coupled Boolean networks with time delay. IEEE Trans Neural Netw Learn Syst 25(12):2288–2294
Shi P, Zhang Y, Chadli M, Agarwal R (2016) Mixed H-infinity and passive filtering for discrete fuzzy neural networks with stochastic jumps and time delays. IEEE Trans Neural Netw Learn Syst 27(4):903–909
Ge SS, Hong F, Lee TH (2004) Adaptive neural control of nonlinear time-delay systems with unknown virtual control coefficients. IEEE Trans Syst Man Cybern B Cybern 34(1):499–516
Yoo SJ, Park JB, Choi YH (2009) Adaptive neural control for a class of strict-feedback nonlinear systems with state time delays. IEEE Trans Neural Netw 20(7):1209–1215
Ho DWC, Li J, Niu Y (2005) Adaptive neural control for a class of nonlinearly parametric time-delay systems. IEEE Trans Neural Netw 16(3):625–635
Shi P, Li F, Wu L, Lim CC (2016) Neural network-based passive filtering for delayed neural-type semi-Markovian jump systems. IEEE Trans Neural Netw Learn Syst. doi:10.1109/TNNLS.2016.2573853
Lu CH, Tai CC, Chen TC, Wang WC (2015) Fuzzy neural network speed estimation method for induction motor speed sensorless control. Int J Innov Comput Inf Control 11(2):433–446
Gao S, Ning B, Dong H (2015) Adaptive neural control with intercepted adaptation for time-delay saturated nonlinear systems. Neural Comput Appl 26(8):1849–1857
Zhao X, Shi P, Zheng X, Zhang J (2016) Intelligent tracking control for a class of uncertain high-order nonlinear systems. IEEE Trans Neural Netw Learn Syst 27(9):1976–1982
Hua C, Yu C, Guan X (2014) Neural network observer-based networked control for a class of nonlinear systems. Neurocomputing 133:103–110
Zhou Q, Shi P, Xu S, Li H (2013) Observer-based adaptive neural network control for nonlinear stochastic systems with time-delay. IEEE Trans Neural Netw Learn Syst 24(1):71–80
Yu Z, Li S, Du H (2014) Adaptive neural output feedback control for stochastic nonlinear time-delay systems with unknown control directions. Neural Comput Appl 25(7):1979–1992
Yu Z, Li S (2014) Neural-network-based output-feedback adaptive dynamic surface control for a class of stochastic nonlinear time-delay systems with unknown control directions. Neurocomputing 129:540–547
Chen W, Jiao L, Li J, Li R (2010) Adaptive NN backstepping output feedback control for stochastic nonlinear strict-feedback systems with time-varying delays. IEEE Trans Syst Man Cybern B Cybern 40(3):939–950
Duan N, Min HF (2016) Decentralized adaptive NN state-feedback control for large-scale stochastic high-order nonlinear systems. Neurocomputing 173(3):1412–1421
Min HF, Duan N, Zhang ZJ (2015) Adaptive output-feedback control for stochastic robot system based on neural network. In: Proceedings of the 34th Chinese control conference. IEEE, Hangzhou, Zhejiang, pp 1839–1844
Min H, Duan N (2015) Adaptive NN state-feedback control for stochastic high-order nonlinear systems with time-varying control direction and delays. Math Probl Eng 2015(723425):1–11
Wang H, Chen B, Lin C (2012) Adaptive neural control for strict-feedback stochastic nonlinear systems with time-delay. Neurocomputing 77:267–274
Qian C, Lin W (2002) Practical output tracking of nonlinear systems with uncontrollable unstable linearization. IEEE Trans Autom Control 47(1):21–36
Hua C, Guan X, Shi P (2005) Robust backstepping control for a class of time delay systems. IEEE Trans Autom Control 50(6):894–899
Acknowledgements
This work is supported by National Natural Science Foundation of China (Nos. 61573172, 61403173, 61503166), 333 High-Level Talents Training Program in Jiangsu Province (No. BRA2015352) and Program for Fundamental Research of Natural Sciences in Universities of Jiangsu Province (No. 15KJB510011) and Jiangsu Province Innovation Program of Graduate Students of China (No. KYCX17_0364).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Appendix
Appendix
Proof of Proposition 1
We prove it by induction. Assume that at step (\(i-1\)), there exist a series of virtual control laws
such that \(U_{i-1}\) satisfies
Now, we prove (52) still holds for (30). Firstly, from (4) and (7), one has
where \(\bar{f}_i=f_i-\sum _{j=1}^{i-1}\frac{\partial \alpha _i}{\partial x_j} (x_{j+1}^{p_j}+f_j)\,-\sum _{j=1}^{i-2}\frac{\partial \alpha _i}{\partial L_j}\dot{L}_j\) and \(\bar{g}_{id}=g_{id}-\sum _{j=1}^{i-1}\frac{\partial \alpha _i}{\partial x_j}g_{jd}\). Choosing Lyapunov function (30) and using (31), (52)–(53), one can get
In the sequel, we focus on estimating the third–fifth terms on the right-hand side of (54). From (2), one gets \(\bar{f}_i(X_i)=W_i^{*^T}S_i(X_i)+\delta _i(X_i)\), \(|\delta _i(X_i)|\le \varepsilon _i\), where \(\varepsilon _i>0\) is a design constant, \(X_i=(\bar{z}_i,\bar{L}_{i-1},\hat{\theta })^T \in S_{X_i}=\{X_i|X_i\in S_x\}\). Then, using \((a+b)^n=\sum _{i=0}^nC_n^ia^{n-i}b^i\), (5)–(7), Lemmas 1 and 2 and \(\Vert W_{i}^{*^T}\Vert ^2\Vert S_{i}\Vert ^2\le \Vert W_{i}^{*^T}\Vert ^2N_{i}\le \theta\), there exist positive constants \(\xi _i\), \(\bar{\gamma }_i=\sum _{j=0}^{\frac{p_i-1}{2}}\gamma _{ij}\), \(\gamma _{ij}\), \(\tilde{\gamma }_i\), and smooth functions \(\lambda _i(\hat{\theta })\), \(\Phi _{i}(\hat{\theta })\), \(\Phi _{i+1,0}(\bar{z}_i,\bar{L}_{i-1},\hat{\theta })\), \(\varrho _{ij}(\bar{z}_{jd})\), \(\varrho _{ii}(\bar{z}_{id},\bar{L}_{i-2,d})\) with \(j=1,\ldots ,i-1\) such that
Finally, by choosing \(U_i\) as (30) and substituting (55)–(57) into (54), one can yield (32). The proof is completed. \(\square\)
Rights and permissions
About this article
Cite this article
Duan, N., Min, H., Shu, Z. et al. A combined NN and dynamic gain-based approach to further stabilize nonlinear time-delay systems. Neural Comput & Applic 31, 2183–2193 (2019). https://doi.org/10.1007/s00521-017-3180-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-017-3180-8