Skip to main content
Springer Nature Link
Log in

Quantum multiverse optimization algorithm for optimization problems

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

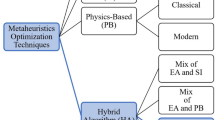
In this paper, a new hybrid algorithm called quantum multiverse optimization (QMVO) is proposed. The proposed QMVO is based on quantum computing and multiverse optimization (MVO) algorithm. The main features of quantum theory and MVO were applied in a new algorithm to find the optimal trade-off between exploration and exploitation. QMVO algorithm depends on adopting a quantum representation of the search space and the integration of the quantum interference and operators in the multiverse optimization algorithm to obtain the optimal solution of the objective function. The performance of QMVO algorithm is evaluated by using 50 unimodal and multimodal benchmark functions. The experimental results show that the proposed algorithm has comprehensive superiority in solving complex numerical optimization problems. Also, the results show that the proposed QMVO is a promising optimization algorithm compared with other well-known and popular algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Abbas N, Aftan H (2014) Quantum artificial bee colony algorithm for numerical function optimization. Int J Comput Appl 93(9):28–30

    Google Scholar 

  2. Benioff P (1980) The computer as a physical system: a microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. J Stat Phys 22(5):563–591

    Article  MathSciNet  MATH  Google Scholar 

  3. Coelho L (2008) A quantum particle swarm optimizer with chaotic mutation operator. Chaos Solitons Fractals 37(5):1409–1418

    Article  Google Scholar 

  4. Derrac J, Garca S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1(1):3–18

    Article  Google Scholar 

  5. Deutsch D (1985) Quantum theory, the Church–Turing principle and the universal quantum computer. Proc R Soc A 400(1818):97–117

    Article  MathSciNet  MATH  Google Scholar 

  6. Digalakis J, Margaritis K (2001) On benchmarking functions for genetic algorithms. Int. J. Comput. Math. 77:481–506

    Article  MathSciNet  MATH  Google Scholar 

  7. Draa A, Meshoul S, Talbi H (2010) Batouche a quantum-inspired differential evolution algorithm for solving the n-queens problem. Int Arab J Inf Technol 7(1):21–27

    Google Scholar 

  8. Du K, Swamy M (2016) Search and optimization by metaheuristics, vol 1. Springer, New York City, p 434

    Book  MATH  Google Scholar 

  9. Faris H, Aljarah I, Mirjalili S (2016) Training feedforward neural networks using multi-verse optimizer for binary classification problems. Appl Intell 45:322–332

    Article  Google Scholar 

  10. Faris H, Hassonah M, Al-Zoubi A, Mirjalili S, Aljarah I (2017) A multi-verse optimizer approach for feature selection and optimizing SVM parameters based on a robust system architecture. Neural Comput Appl 1–15

  11. Gottfried K, Yan T (2003) Quantum mechanics: fundamentals, vol. 2. Springer-Verlag, New York

  12. Han K, Kim J (2002) Quantum-inspired evolutionary algorithm for a class of combinatorial optimization. IEEE Trans Evol Comput 6(6):580–93

    Article  MathSciNet  Google Scholar 

  13. Han K, Kim J (2004) Quantum-inspired evolutionary algorithms with a new termination criterion, h epsi; gate, and two-phase scheme. IEEE Trans Evol Comput 8(2):156–169

    Article  MathSciNet  Google Scholar 

  14. Han KH, Kim JH (1997) No free lunch theorems for optimization. IEEE Trans Evol Comput 1:67–82

    Article  Google Scholar 

  15. Herrera B, Coelho L, Steiner M (2015) Quantum inspired particle swarm combined with Lin–Kernighan–Helsgaun method to the traveling salesman problem. Pesquisa Operacional 35:465–488

    Article  Google Scholar 

  16. Jamil M, Yang X (2013) A literature survey of benchmark functions for global optimization problems. Int J Math Model Numer Optim 4(2):150–194

    MATH  Google Scholar 

  17. Jangir P, Parmar S, Trivedi I, Bhesdadiya R (2017) A novel hybrid particle swarm optimizer with multi verse optimizer for global numerical optimization and optimal reactive power dispatch problem. Eng Sci Technol Int J 20(2):570–586

    Article  Google Scholar 

  18. Jiao L, Li Y, Gong M, Zhang X (2008) Quantum-inspired immune clonal algorithm for global optimization. IEEE Trans Syst Man Cybern Part B Cybern 38(5):1234–1253

    Article  Google Scholar 

  19. Jing L, Wenbo X, Jun S (2005) Quantum-behaved particle swarm optimization with mutation operator. In: 17th IEEE international conference on tools with artificial intelligence (ICTAI’05), pp 240–244

  20. Jun S, Wenbo X, Bin F (2005) Adaptive parameter control for quantum-behaved particle swarm optimization on individual level. In: IEEE international conference on systems, man and cybernetics, vol 4, pp 3049–3054

  21. Kennedy J, Eberhart R(1995) Particle swarm optimization. In: IEEE international conference on neural networks, Perth, WA, pp 1942–1948

  22. Layeb A (2010) Hybrid quantum scatter search algorithm for combinatorial optimization problems. J Ann Comput Sci Ser 8(2):227–244

    Google Scholar 

  23. Layeb A (2013) A hybrid quantum inspired harmony search algorithm for 0–1 optimization problems. J Comput Appl Math 253:14–25

    Article  MathSciNet  MATH  Google Scholar 

  24. Layeb A, Saidouni DE (2004) A new quantum evolutionary local search algorithm forMAX3-SAT problem. In: Proceedings of the 3rd international workshop on hybrid artificial intelligence systems, Lecture notes in artificial intelligence, vol 5271. Springer, Berlin, pp 172–179

  25. Layeb A, Saidouni DE (2010) A new quantum evolutionary algorithm with sifting strategy for binary decision diagram ordering problem. Int J Cogn Inform Nat Intell 4(4):47–61

    Article  Google Scholar 

  26. Meng X, Liu Y, Gao X, Zhang H (2014) A new bio-inspired algorithm: chicken swarm optimization. In: Advances in swarm intelligence: 5th international conference, ICSI, Cham, pp 86–94

  27. Meng X, Liu Y, Gao X, Zhang H (2014) A new bio-inspired algorithm: chicken swarm optimization. In: Advances in swarm intelligence: 5th international conference, ICSI, Cham, pp 86–94

  28. Mirjalili S (2015) Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl Based Syst 89:228–249

    Article  Google Scholar 

  29. Mirjalili S (2016) SCA: a sine cosine algorithm for solving optimization problems. Knowl Based Syst 96:120–130

    Article  Google Scholar 

  30. Mirjalili S, Mirjalili SM, Hatamlou A (2016) Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput Appl 27(2):495–513

    Article  Google Scholar 

  31. Mirjalili S, Seyed M, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61

    Article  Google Scholar 

  32. Molga M, Smutnicki C (2005) Test functions for optimization needs. unpublished paper

  33. Montanaro A (2016) Quantum algorithms: an overview. npj Quantum Inf 2:1–8

    Article  Google Scholar 

  34. Narayanan A, Moore M (1996) Quantum-inspired genetic algorithms. In: Proceedings of IEEE international conference on evolutionary computation, Nogaya, Japan, pp 61–66

  35. Rehman O, Yang S, Khan S (2017) A modified quantum-based particle swarm optimization for engineering inverse problem. COMPEL Int J Comput Math Electr Electron Eng 36:168–187

    Article  Google Scholar 

  36. Shor P (1997) Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J Sci Stat Comput 26:1484–1509

    Article  MathSciNet  MATH  Google Scholar 

  37. Sun J, Feng B, Xu W (2004) Particle swarm optimization with particles having quantum behavior. In: Congress on evolutionary computation, vol 1, pp 325–331

  38. Surjanovic S, Bingham D (2016) Virtual library of simulation experiments: test functions and datasets. Retrieved September 25 from http://www.sfu.ca/~ssurjano

  39. Tegmark M (2004) Science and ultimate reality: quantum theory, cosmology, and complexity. Cambridge Unversity Press, Cambridge, UK, pp 459–491

    Book  Google Scholar 

  40. Wilcoxon F (1945) Individual comparisons by ranking methods. Biom Bull 1:80–83

    Article  Google Scholar 

  41. Wolpert D, Macready W (2004) Quantum-inspired evolutionary algorithms with a new termination criterion, h gate, and two phase scheme. IEEE Trans Evol Comput 8(2):156–169

    Article  Google Scholar 

  42. Yang X-S (2010) Test problems in optimization. Wiley, London, pp 261–266

    Google Scholar 

  43. Yang XS, Cui ZH, Xiao RB, Gandomi AH, Karamanoglu M (2013) Swarm intelligence and bio-inspired computation. Elsevier Science Publishers BV, Amsterdam, The Netherlands, The Netherlands, pp 3–23

    Book  Google Scholar 

  44. Yao X, Liu Y, Lin G (1999) Evolutionary programming made faster. IEEE Trans Evol Comput 3:82–102

    Article  Google Scholar 

  45. Ykhlef M (2011) A quantum swarm evolutionary algorithm for mining association rules in large databases. J King Saud Univ Comput Inf Sci 23:1–6

    Article  Google Scholar 

  46. Zouache A, Moussaoui A (2015) Quantum-inspired differential evolution with particle swarm optimization for knapsack problem. J Inf Sci Eng 31:1757–1773

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Computers and Information, Cairo University, Cairo, Egypt

    Gehad Ismail Sayed & Aboul Ella Hassanien

  2. Faculty of Science, Helwan University, Cairo, Egypt

    Ashraf Darwish

  3. Scientific Research Group in Egypt, Cairo, Egypt

    Gehad Ismail Sayed, Ashraf Darwish & Aboul Ella Hassanien

Authors
  1. Gehad Ismail Sayed
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ashraf Darwish
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Aboul Ella Hassanien
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Gehad Ismail Sayed.

Ethics declarations

Conflicts of interest

We declare that we have no significant competing financial, professional or personal interests that might have influenced the performance or presentation of the work described in this manuscript.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sayed, G.I., Darwish, A. & Hassanien, A.E. Quantum multiverse optimization algorithm for optimization problems. Neural Comput & Applic 31, 2763–2780 (2019). https://doi.org/10.1007/s00521-017-3228-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-017-3228-9

Keywords