Non-negative enhanced discriminant matrix factorization method with sparsity regularization

Abstract

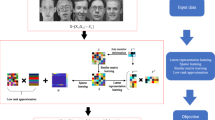
Efficient low-rank representation of data plays a significant role in the field of computer vision and pattern recognition. In order to obtain a more discriminant and sparse low-dimensional representation, a novel non-negative enhanced discriminant matrix factorization method with sparsity regularization is proposed in this paper. Firstly, the local invariance and discriminant information of the low-dimensional representation are incorporated into the objective function to construct a new within-class encouragement constraint term, and the weighted coefficients are introduced to further enhance the compactness between the samples that belong to the same class in the new base space. Secondly, a new between-class penalty term is constructed to maximize the difference between different classes of samples, and meanwhile, the weighted coefficients are introduced to further enhance the discreteness and discriminativeness between classes. Finally, to learn the part-based representation of data better, the sparse constraint term is further introduced, and consequently, the sparseness of data representation, the local invariance, and the discriminativeness are integrated into a unified framework. Moreover, the optimization solution and the convergence proof of objective function are given. The extensive experiments demonstrate the strong robustness of the proposed method to face recognition and image classification under occlusions.

Appendix: Proof of Theorem 1

To prove Theorem 1, it is necessary to show the nonincreasing property of objective function in Eq. (14) under the iteration rules in Eqs. (20) and (21). As the iteration rule of Eq. (20) is identical to original NMF, the convergence proof of NMF can be adopted to manifest that objective function is nonincreasing under the iteration rule in Eq. (20), and it is only needed to prove that the objective function is nonincreasing under Eq. (21). An auxiliary function approximate to that utilized in the Expectation Maximization (EM) algorithm is adopted in the proof process.

Definition 1

If the conditions $G(M,M^{(t)} ) \ge F(M),G(M,M) = F(M)$ hold, then $G(M,M^{(t)} )$ is an auxiliary function of $F(M)$.

Lemma 1

If$G(M,M^{(t)} )$is an auxiliary function of$F(M)$, then$F(M)$is nonincreasing under the following update condition.

$$ M^{(t + 1)} = \arg \min_{M} G(M,M^{(t)} ) $$

(26)

Proof

$F(M^{(t + 1)} ) \le G(M^{(t + 1)} ,M^{(t)} ) \le G(M^{(t)} ,M^{(t)} ) = F(M^{(t)} )$.

Lemma 2

Function$G({\mathbf{H}}(k),{\mathbf{H}}^{(t)} (k))$, namely an auxiliary function of$F({\mathbf{H}}(k))$, and$F({\mathbf{H}}(k))$are given by Eqs. (27) and (28), respectively:

$$ \begin{aligned} G({\mathbf{H}}(k),{\mathbf{H}}^{(t)} (k)) & = \sum\limits_{i,j} {\left( {B_{i,j} (k)\log B_{i,j} (k) - B_{i,j} (k)} \right)} - \sum\limits_{i,j} {B_{i,j} (k)} \sum\limits_{m} {\left( {\frac{{Z_{i,m} (k)H_{m,j}^{(t)} (k)}}{{\sum\limits_{m} {Z_{i.m} (k)H_{m,j}^{(t)} (k)} }}} \right.} \\ & \quad \times \left. {\left( {\log (Z_{i,m} (k)H_{m,j} (k)) - \log \frac{{Z_{i,m} (k)H_{m,j}^{(t)} (k)}}{{\sum\limits_{m} {Z_{i.m} (k)H_{m,j}^{(t)} (k)} }}} \right)} \right){ + }\sum\limits_{i,j,k} {Z_{i,m} (k)H_{m,j} (k)} \\ & \quad { + }\gamma \sum\limits_{i = 1}^{C} {\sum\limits_{j \ne m}^{{N_{i} }} {\frac{{rat_{i} }}{{N_{i} (N_{i} - 1)}}\left\| {{\varvec{\upeta}}_{j}^{(i)} (k) - {\varvec{\upeta}}_{m}^{(i)} (k)} \right\|_{2}^{2} } } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \lambda \sum\limits_{i,j} {H_{i,j} (k)} \\ & \quad - \frac{\delta }{C(C - 1)}\sum\limits_{i \ne j}^{C} {W^{\prime}_{i,j} (k)\left\| {{\varvec{\upmu}}^{(i)} (k) - {\varvec{\upmu}}^{(j)} (k)} \right\|_{2}^{2} } \\ \end{aligned} $$

(27)

$$ \begin{aligned} F\left( {{\mathbf{H}}(k)} \right) = D_{NEDMF\_SR} & = \sum\limits_{i,j} {\left( {B_{i,j} (k)\log \frac{{B_{i,j} (k)}}{{\left( {{\mathbf{Z}}(k){\mathbf{H}}(k)} \right)_{i,j} }} - B_{i,j} (k) + ({\mathbf{Z}}(k){\mathbf{H}}(k))_{i,j} } \right)} \\ {\kern 1pt} & \quad + \gamma \sum\limits_{i = 1}^{C} {\sum\limits_{j \ne m}^{{N_{i} }} {\frac{{rat_{i} }}{{N_{i} (N_{i} - 1)}}\left\| {{\varvec{\upeta}}_{j}^{(i)} (k) - {\varvec{\upeta}}_{m}^{(i)} (k)} \right\|_{2}^{2} } } \\ & \quad - \frac{\delta }{C(C - 1)}\sum\limits_{{{\kern 1pt} i \ne j}}^{C} {W^{\prime}_{i,j} (k)\left\| {{\varvec{\upmu}}^{(i)} (k) - {\varvec{\upmu}}^{(j)} (k)} \right\|_{2}^{2} } \\ & \quad + \lambda \sum\limits_{i,j} {H_{i,j} (k)} \\ \end{aligned} $$

(28)

Proof

It is easy to find that $G({\mathbf{H}}(k),{\mathbf{H}}(k)) = F({\mathbf{H}}(k))$. According to Lemma 1, it is only need to show $G({\mathbf{H}}(k),{\mathbf{H}}^{(t)} (k)) \ge F({\mathbf{H}}(k))$ to prove that $G({\mathbf{H}}(k),{\mathbf{H}}^{(t)} (k))$ is an auxiliary function of $F({\mathbf{H}}(k))$.

Due to the convexity of $\log \left( {\sum\nolimits_{m} {Z_{i,m} (k)H_{m,j} (k)} } \right)$, the following inequality holds for each non-negative element $a_{m}$, all of which subject to the condition of $\sum\nolimits_{m} {a_{m} = 1}$.

$$ - \log \left( {\sum\limits_{m} {Z_{i,m} (k)H_{m,j} (k)} } \right) \le - \sum\limits_{m} {a_{m} \log \frac{{Z_{i,m} (k)H_{m,j} (k)}}{{a_{m} }}} $$

(29)

Assume $a_{m} = Z_{i,m} (k)H_{m,j}^{(t)} (k) \ \sum\nolimits_{m} Z_{i,m}(k)H_{m,j}^{(t)} (k)$, Eq. (29) can be transformed as follows:

$$ - \log \left( {\sum\limits_{m} {Z_{i,m} (k)H_{m,j} (k)} } \right) \le - \sum\nolimits_{k} {\frac{{Z_{i,m} (k)H_{m,j}^{(t)} (k)}}{{\sum\limits_{k} {Z_{i,m} (k)H_{m,j}^{(t)} (k)} }}\left( {\log \left( {Z_{i,m} (k)H_{m,j} (k)} \right) - \log \frac{{Z_{i,m} (k)H_{m,j}^{(t)} (k)}}{{\sum\nolimits_{m} {Z_{i,m} (k)H_{m,j}^{(t)} (k)} }}} \right)} $$

(30)

From Eq. (30), it is easily observed that $G({\mathbf{H}}(k),{\mathbf{H}}^{(t)} (k)) \ge F({\mathbf{H}}(k))$. Consequently, $G({\mathbf{H}}(k),{\mathbf{H}}^{(t)} (k))$ can be viewed as an auxiliary function of $F({\mathbf{H}}(k))$.

Proof of Theorem 1

The minimum of $G({\mathbf{H}}(k),{\mathbf{H}}^{(t)} (k))$ in regard to $H_{m,l} (k)$ is obtained by setting the gradient to zero:

$$ \begin{aligned} \frac{{\partial G({\mathbf{H}}(k),{\mathbf{H}}^{(t)} (k))}}{{\partial H_{m,l} (k)}} & = - \sum\nolimits_{i} {{{B}}_{i,l} (k)\frac{{Z_{i,m} (k)H_{m,l}^{(t)} (k)}}{{\sum\nolimits_{n} {Z_{i,n} (k)H_{n,l}^{(t)} (k)} }}} \frac{1}{{H_{m,l} (k)}} \\ & \quad + \sum\nolimits_{i} {Z_{i,m} (k)} + \frac{{4rat_{r} \gamma }}{{N_{r} - 1}}\left( {H_{m,l} (k) - \mu_{m}^{(r)} (k)} \right) \\ & \quad - \frac{{4\delta W^{\prime}_{i,r} \left( k \right)}}{{N_{r} C\left( {C - 1} \right)}}\sum\limits_{i \ne r}^{C} {\left( {\mu_{m}^{(r)} (k) - \mu_{m}^{(i)} (k)} \right)} + \lambda \\ & = 0 \\ \end{aligned} $$

(31)

The above equation is a quadratic equation of $H_{m,l} (k)$, and by solving it, the iterative rule of Eq. (20) can be obtained. According to Lemma 1, now that $G({\mathbf{H}}(k),{\mathbf{H}}^{(t)} (k))$ is an auxiliary function, and then, the function $F({\mathbf{H}}(k))$, i.e., $D_{NEDMF\_SR}$, is nonincreasing under the iterative rule in Eq. (20).