Skip to main content
Springer Nature Link
Log in

A machine-learning-enhanced hierarchical multiscale method for bridging from molecular dynamics to continua

  • Extreme Learning Machine and Deep Learning Networks
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

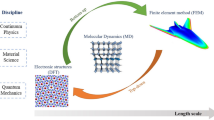
Abstract

In the community of computational materials science, one of the challenges in hierarchical multiscale modeling is information-passing from one scale to another, especially from the molecular model to the continuum model. A machine-learning-enhanced approach, proposed in this paper, provides an alternative solution. In the developed hierarchical multiscale method, molecular dynamics simulations in the molecular model are conducted first to generate a dataset, which represents physical phenomena at the nanoscale. The dataset is then used to train a material failure/defect classification model and stress regression models. Finally, the well-trained models are implemented in the continuum model to study the mechanical behaviors of materials at the macroscale. Multiscale modeling and simulation of a molecule chain and an aluminum crystalline solid are presented as the applications of the proposed method. In addition to support vector machines, extreme learning machines with single-layer neural networks are employed due to their computational efficiency.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Abraham FF, Broughton JQ, Bernstein N, Kaxiras E (1998) Spanning the length scales in dynamic simulation. Comput Phys 12(6):538–546

    Google Scholar 

  2. Ademiloye A, Zhang L, Liew K (2017) Atomistic-continuum model for probing the biomechanical properties of human erythrocyte membrane under extreme conditions. Comput Methods Appl Mech Eng 325:22–36

    MathSciNet  MATH  Google Scholar 

  3. Akusok A, Bjork KM, Miche Y, Lendasse A (2015) High-performance extreme learning machines: a complete toolbox for big data applications. IEEE Access 3:1011–1025

    Google Scholar 

  4. Arroyo M, Belytschko T (2003) A finite deformation membrane based on inter-atomic potentials for the transverse mechanics of nanotubes. Mech Mater 35(3–6):193–215

    Google Scholar 

  5. Artrith N, Urban A (2016) An implementation of artificial neural-network potentials for atomistic materials simulations: performance for TiO 2. Comput Mater Sci 114:135–150

    Google Scholar 

  6. Badia S, Bochev P, Lehoucq R, Parks ML, Fish J, Nuggehally MA, Gunzburger M (2007) A Force-Based Blending Model forAtomistic-to-Continuum Coupling. Int J Multiscale Comput Eng 5(5):387–406

    Google Scholar 

  7. Bélisle E, Huang Z, Le Digabel S, Gheribi AE (2015) Evaluation of machine learning interpolation techniques for prediction of physical properties. Comput Mater Sci 98:170–177

    Google Scholar 

  8. Bogdanor MJ, Oskay C, Clay SB (2015) Multiscale modeling of failure in composites under model parameter uncertainty. Comput Mech 56(3):389–404

    MathSciNet  MATH  Google Scholar 

  9. Chen C, Deng Z, Tran R, Tang H, Chu IH, Ong SP (2017) Accurate force field for molybdenum by machine learning large materials data. Phys Rev Mater 1(4):043603

    Google Scholar 

  10. Chen S, Cowan C, Grant P (1991) Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans Neural Netw 2(2):302–309

    Google Scholar 

  11. Hsu Chih-Wei, Lin Chih-Jen (2002) A comparison of methods for multiclass support vector machines. IEEE Trans Neural Netw 13(2):415–425

    Google Scholar 

  12. Cortes C, Vapnik V (1995) Support-vector networks. Mach Learn 20(3):273–297

    MATH  Google Scholar 

  13. Curtin WA, Miller RE (2003) Atomistic/continuum coupling in computational materials science. Modell Simul Mater Sci Eng 11(3):R33–R68

    Google Scholar 

  14. Ericksen J (1984) The Cauchy and Born hypotheses for crystals. In: Phase Transformations and Material Instabilities in Solids. Elsevier, pp 61–77

  15. Fish J (2006) Bridging the scales in nano engineering and science. J Nanopart Res 8(5):577–594

    Google Scholar 

  16. Fritzen F, Kunc O (2018) Two-stage data-driven homogenization for nonlinear solids using a reduced order model. Eur J Mech A Solids 69:201–220

    MathSciNet  MATH  Google Scholar 

  17. Ghaffari MA, Zhang Y, Xiao S (2018) Multiscale modeling and simulation of rolling contact fatigue. Int J Fatigue 108:9–17

    Google Scholar 

  18. Glielmo A, Sollich P, De Vita A (2017) Accurate interatomic force fields via machine learning with covariant kernels. Phys Rev B 95(21):214302

    Google Scholar 

  19. Goodfellow I, Bengio Y, Courville A (2016) Deep learning. MIT Press, Cambridge

    MATH  Google Scholar 

  20. Grabowski K, Zbyrad P, Uhl T, Staszewski WJ, Packo P (2017) Multiscale electro-mechanical modeling of carbon nanotube composites. Comput Mater Sci 135:169–180

    Google Scholar 

  21. Gracie R, Belytschko T (2011) An adaptive concurrent multiscale method for the dynamic simulation of dislocations. Int J Numer Meth Eng 86(4–5):575–597

    MATH  Google Scholar 

  22. Huang G-B, Zhu Q-Y, Siew C-K (2004) Extreme learning machine: a new learning scheme of feedforward neural networks. In: IEEE international joint conference on neural networks (IEEE Cat. No.04CH37541), vol 2. IEEE, pp 985–990

  23. Gupta A, Cecen A, Goyal S, Singh AK, Kalidindi SR (2015) Structure-property linkages using a data science approach: application to a non-metallic inclusion/steel composite system. Acta Mater 91:239–254

    Google Scholar 

  24. Hansen K, Biegler F, Ramakrishnan R, Pronobis W, von Lilienfeld OA, Müller KR, Tkatchenko A (2015) Machine learning predictions of molecular properties: accurate many-body potentials and nonlocality in chemical space. J Phys Chem Lett 6(12):2326–2331

    Google Scholar 

  25. Hornik K, Stinchcombe M, White H (1989) Multilayer feedforward networks are universal approximators. Neural Netw 2(5):359–366

    MATH  Google Scholar 

  26. Hu R, Roshdibenam V, Johnson HJ, Eirola E, Akusok A, Miche Y, Björk KM, Lendasse A (2018) Elm-som: A continuous self-organizing map for visualization. In: International joint conference on neural networks (IJCNN). IEEE, pp 1–8

  27. Huang G, Huang GB, Song S, You K (2015) Trends in extreme learning machines: a review. Neural Netw 61:32–48

    MATH  Google Scholar 

  28. Huang GB (2014) An insight into extreme learning machines: random neurons random features and kernels. Cogn Comput 6(3):376–390

    MathSciNet  Google Scholar 

  29. Huang GB (2015) What are extreme learning machines? Filling the gap between Frank Rosenblatt’s dream and John von Neumann’s puzzle. Cogn Comput 7:263–278

    Google Scholar 

  30. Huang GB, Zhu QY, Siew CK (2006) Extreme learning machine: theory and applications. Neurocomputing 70(1–3):489–501

    Google Scholar 

  31. Ibañez R, Abisset-Chavanne E, Aguado JV, Gonzalez D, Cueto E, Chinesta F (2018) A manifold learning approach to data-driven computational elasticity and inelasticity. Arch Comput Methods Eng 25(1):47–57

    MathSciNet  MATH  Google Scholar 

  32. Ibañez R, Borzacchiello D, Aguado JV, Abisset-Chavanne E, Cueto E, Ladeveze P, Chinesta F (2017) Data-driven non-linear elasticity: constitutive manifold construction and problem discretization. Comput Mech 60(5):813–826

    MathSciNet  MATH  Google Scholar 

  33. Igelnik B, Pao YH (1995) Stochastic choice of basis functions in adaptive function approximation and the functional-link net. IEEE Trans Neural Networks 6(6):1320–1329

    Google Scholar 

  34. Jahya A, Herink M, Misra S (2013) A framework for predicting three-dimensional prostate deformation in real time. Int J Med Robot Comput Assist Surg 9(4):e52–e60

    Google Scholar 

  35. Jain A, Hautier G, Ong SP, Persson K (2016) New opportunities for materials informatics: resources and data mining techniques for uncovering hidden relationships. J Mater Res 31(08):977–994

    Google Scholar 

  36. Jiang S, Tao J, Sewell TD, Chen Z (2017) Hierarchical multiscale simulations of crystalline \(\beta\)-octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (\(\beta\)-HMX): Generalized interpolation material point method simulations of brittle fracture using an elastodamage model derived from molecular dynamics. Int J Damage Mech 26(2):293–313

    Google Scholar 

  37. Kalidindi SR, Niezgoda SR, Salem AA (2011) Microstructure informatics using higher-order statistics and efficient data-mining protocols. JOM 63(4):34–41

    Google Scholar 

  38. Kelchner CL, Plimpton SJ, Hamilton JC (1998) Dislocation nucleation and defect structure during surface indentation. Phys Rev B 58(17):11085–11088

    Google Scholar 

  39. Le BA, Yvonnet J, He QC (2015) Computational homogenization of nonlinear elastic materials using neural networks. Int J Numer Meth Eng 104(12):1061–1084

    MathSciNet  MATH  Google Scholar 

  40. Lendasse A, Wertz V, Verleysen M (2003) Model selection with cross-validations and bootstraps—application to time series prediction with RBFN models. In: Xu L, Kaynak O, Alpaydin E, Oja E (ed) Artificial neural networks and neural information processing—ICANN/ICONIP 2003. Lecture notes in computer science, vol 2714. Springer, Berlin, pp 573–580

  41. Liu W, Karpov E, Zhang S, Park H (2004) An introduction to computational nanomechanics and materials. Comput Methods Appl Mech Eng 193(17–20):1529–1578

    MathSciNet  MATH  Google Scholar 

  42. Liu WK, Qian D, Gonella S, Li S, Chen W, Chirputkar S (2010) Multiscale methods for mechanical science of complex materials: Bridging from quantum to stochastic multiresolution continuum. Int J Numer Meth Eng 83(8–9):1039–1080

    MATH  Google Scholar 

  43. Liu Z, Bessa M, Liu WK (2016) Self-consistent clustering analysis: an efficient multi-scale scheme for inelastic heterogeneous materials. Comput Methods Appl Mech Eng 306:319–341

    MathSciNet  MATH  Google Scholar 

  44. Liu Z, Fleming M, Liu WK (2018) Microstructural material database for self-consistent clustering analysis of elastoplastic strain softening materials. Comput Methods Appl Mech Eng 330:547–577

    MathSciNet  MATH  Google Scholar 

  45. Lorente D, Martínez-Martínez F, Rupérez M, Lago M, Martínez-Sober M, Escandell-Montero P, Martínez-Martínez J, Martínez-Sanchis S, Serrano-López A, Monserrat C, Martín-Guerrero J (2017) A framework for modelling the biomechanical behaviour of the human liver during breathing in real time using machine learning. Expert Syst Appl 71:342–357

    Google Scholar 

  46. Marcus G (2018) Deep learning: a critical appraisal. arXiv preprint arXiv:1801.00631

  47. Matouš K, Geers MG, Kouznetsova VG, Gillman A (2017) A review of predictive nonlinear theories for multiscale modeling of heterogeneous materials. J Comput Phys 330:192–220

    MathSciNet  Google Scholar 

  48. McDowell DL, Panchal J, Choi HJ, Seepersad C, Allen J, Mistree F (2010) Integrated design of multiscale, multifunctional materials and products, 1st edn. Butterworth-Heinemann, Oxford

    Google Scholar 

  49. Meng Q, Li B, Li T, Feng XQ (2017) A multiscale crack-bridging model of cellulose nanopaper. J Mech Phys Solids 103:22–39

    MathSciNet  Google Scholar 

  50. Mielke SL, Troya D, Zhang S, Li JL, Xiao S, Car R, Ruoff RS, Schatz GC, Belytschko T (2004) The role of vacancy defects and holes in the fracture of carbon nanotubes. Chem Phys Lett 390(4–6):413–420

    Google Scholar 

  51. Miller RE, Tadmor EB (2009) A unified framework and performance benchmark of fourteen multiscale atomistic/continuum coupling methods. Modell Simul Mater Sci Eng 17(5):053001

    Google Scholar 

  52. Mishin Y, Farkas D, Mehl MJ, Papaconstantopoulos DA (1999) Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. Phys Rev B 59(5):3393–3407

    Google Scholar 

  53. Plimpton S (1995) Fast parallel algorithms for short-range molecular dynamics. J Comput Phys 117(1):1–19

    MATH  Google Scholar 

  54. Rahman MM, Feng Y, Yankeelov TE, Oden JT (2017) A fully coupled space-time multiscale modeling framework for predicting tumor growth. Comput Methods Appl Mech Eng 320:261–286

    MathSciNet  MATH  Google Scholar 

  55. Reich Y, Barai S (1999) Evaluating machine learning models for engineering problems. Artif Intell Eng 13(3):257–272

    Google Scholar 

  56. Rosenblatt F (1958) The perceptron: a probabilistic model for information storage and organization in the brain. Psychol Rev 65(6):386–408

    Google Scholar 

  57. Smola AJ, Schölkopf B (2004) A tutorial on support vector regression. Stat Comput 14(3):199–222

    MathSciNet  Google Scholar 

  58. Song JH, Areias PMA, Belytschko T (2006) A method for dynamic crack and shear band propagation with phantom nodes. Int J Numer Meth Eng 67(6):868–893

    MATH  Google Scholar 

  59. Subramanian N, Rai A, Chattopadhyay A (2015) Atomistically informed stochastic multiscale model to predict the behavior of carbon nanotube-enhanced nanocomposites. Carbon 94:661–672

    Google Scholar 

  60. Tadmor E, Phillips R, Ortiz M (2000) Hierarchical modeling in the mechanics of materials. Int J Solids Struct 37(1–2):379–389

    MathSciNet  MATH  Google Scholar 

  61. Tadmor EB, Miller RE (2017) Benchmarking, validation and reproducibility of concurrent multiscale methods are still needed. Modell Simul Mater Sci Eng 25(7):071001

    Google Scholar 

  62. Tadmor EB, Ortiz M, Phillips R (1996) Quasicontinuum analysis of defects in solids. Philos Mag A 73(6):1529–1563

    Google Scholar 

  63. Talebi H, Silani M, Rabczuk T (2015) Concurrent multiscale modeling of three dimensional crack and dislocation propagation. Adv Eng Softw 80:82–92

    Google Scholar 

  64. Tschopp M, McDowell D (2008) Influence of single crystal orientation on homogeneous dislocation nucleation under uniaxial loading. J Mech Phys Solids 56(5):1806–1830

    MATH  Google Scholar 

  65. Tsoumakas G, Katakis I (2007) Multi-label classification: an overview. Int J Data Wareh Min 3(3):1–13

    Google Scholar 

  66. Wagner GJ, Liu WK (2003) Coupling of atomistic and continuum simulations using a bridging scale decomposition. J Comput Phys 190(1):249–274

    MATH  Google Scholar 

  67. Xiao S (2006) A non-oscillatory method for spallation studies. Int J Numer Meth Eng 66:364–380

    MATH  Google Scholar 

  68. Xiao S, Andersen DR, Han R, Hou W (2006) Studies of carbon nanotube-based oscillators using molecular dynamics. J Comput Theor Nanosci 3(1):142–147

    Google Scholar 

  69. Xiao S, Andersen DR, Yang W (2008) Design and analysis of nanotube-based memory cells. Nanoscale Res Lett 3:416–420

    Google Scholar 

  70. Xiao S, Belytschko T (2004) A bridging domain method for coupling continua with molecular dynamics. Comput Methods Appl Mech Eng 193(17–20):1645–1669

    MathSciNet  MATH  Google Scholar 

  71. Xiao S, Hou W (2006) Fracture of vacancy-defected carbon nanotubes and their embedded nanocomposites. Phys Rev B 73(11):115406

    Google Scholar 

  72. Xiao S, Hou W (2007) Studies of nanotube-based resonant oscillators through multiscale modeling and simulation. Phys Rev B 75(12):125414

    Google Scholar 

  73. Xiao S, Wang S, Ni J, Briggs R, Rysz M (2008) Reliability analysis of carbon nanotubes using molecular dynamics with the aid of grid computing. J Comput Theor Nanosci 5(4):528–534

    Google Scholar 

  74. Xiao S, Yang W (2006) Temperature-related Cauchy-Born rule for multiscale modeling of crystalline solids. Comput Mater Sci 37(3):374–379

    Google Scholar 

  75. Xiao S, Yang W (2007) A temperature-related homogenization technique and its implementation in the meshfree particle method for nanoscale simulations. Int J Numer Meth Eng 69(10):2099–2125

    MathSciNet  MATH  Google Scholar 

  76. Yang W, Xiao S (2008) Extension of the temperature-related Cauchy–Born rule: material stability analysis and thermo-mechanical coupling. Comput Mater Sci 41(4):431–439

    Google Scholar 

  77. Zhou M (2003) A new look at the atomic level virial stress: on continuum-molecular system equivalence. Proc R Soc A: Math Phys Eng Sci 459(2037):2347–2392

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, The University of Iowa, Iowa City, USA

    Shaoping Xiao & Siamak Attarian

  2. Department of Industrial and System Engineering, The University of Iowa, Iowa City, USA

    Renjie Hu & Zhen Li

  3. Arcada University of Applied Sciences, Helsinki, Finland

    Kaj-Mikael Björk & Amaury Lendasse

  4. Hanken School of Economics, Helsinki, Finland

    Kaj-Mikael Björk

  5. Information and Logistics Technology Department, The University of Houston, Houston, USA

    Amaury Lendasse

Authors
  1. Shaoping Xiao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Renjie Hu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zhen Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Siamak Attarian
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Kaj-Mikael Björk
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Amaury Lendasse
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Renjie Hu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xiao, S., Hu, R., Li, Z. et al. A machine-learning-enhanced hierarchical multiscale method for bridging from molecular dynamics to continua. Neural Comput & Applic 32, 14359–14373 (2020). https://doi.org/10.1007/s00521-019-04480-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-019-04480-7

Keywords