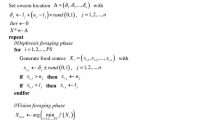Skip to main content

Advertisement

Springer Nature Link
Log in

An improved evolution fruit fly optimization algorithm and its application

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

Fruit fly optimization algorithm (FOA) is a kind of swarm intelligence optimization algorithm, which has been widely applied in science and engineering fields. The aim of this study is to design an improved FOA, namely evolution FOA (EFOA), which can overcome some shortcomings of basic FOA, including difficulty in local optimization, slow convergence speed, and lack of robustness. EFOA applies a few new strategies which adaptively control the search steps and swarm numbers of the fruit flies. The evolution mechanism used in EFOA can preserve dominant swarms and remove inferior swarms. Comprehensive comparison experiments are performed to compare EFOA with other swarm intelligence algorithms through 14 benchmark functions and a constrained engineering problem. Experimental results suggest that EFOA performs well both in global search ability and in robustness, and it can improve convergence speed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Ali ES (2015) Speed control of DC series motor supplied by photovoltaic system via firefly algorithm. Neural Comput Appl 26(6):1321–1332

    Google Scholar 

  2. Abd-Elazim SM, Ali ES (2018) Load frequency controller design of a two-area system composing of PV grid and thermal generator via firefly algorithm. Neural Comput Appl 30(2):607–616

    Google Scholar 

  3. Oshaba AS, Ali ES, Elazim SMA (2017) Pi controller design for MPPT of photovoltaic system supplying SRM via bat search algorithm. Neural Comput Appl 28(4):651–667

    Google Scholar 

  4. Huo J, Liu L (2018) Application research of multi-objective artificial bee colony optimization algorithm for parameters calibration of hydrological model. Neural Comput Appl 31(9): 4715–4732

    Google Scholar 

  5. Chen B, Zhang H, Li M (2019) Prediction of pk(a) values of neutral and alkaline drugs with particle swarm optimization algorithm and artificial neural network. Neural Comput Appl. https://doi.org/10.1007/s00521-018-3956-5

    Article  Google Scholar 

  6. Pan WT (2012) A new fruit fly optimization algorithm: taking the financial distress model as an example. Knowl Based Syst 26(2):69–74

    Google Scholar 

  7. Pan WT (2013) Using modified fruit fly optimisation algorithm to perform the function test and case studies. Connect Sci 25(2–3):151–160

    Google Scholar 

  8. Duan Q, Mao M, Duan P, Hu B (2016) An improved artificial fish swarm algorithm optimized by particle swarm optimization algorithm with extended memory. Kybernetes 45(2):210–222

    Google Scholar 

  9. Jovanovic R, Tuba M, Vo S (2015) An ant colony optimization algorithm for partitioning graphs with supply and demand. Comput Sci 209(3):207–212

    Google Scholar 

  10. Sharma H, Bansal JC, Arya KV (2013) Opposition based levy flight artificial bee colony. Memet Comput 5(3):1–15

    Google Scholar 

  11. Chen PW, Lin WY, Huang TH, Pan WT (2013) Using fruit fly optimization algorithm optimized grey model neural network to perform satisfaction analysis for e-business service. Appl Math Inf Sci 7(2L):459–465

    Google Scholar 

  12. Li HZ, Guo S, Li CJ, Sun JQ (2013) A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl Based Syst 37(2):378–387

    Google Scholar 

  13. Sheng W, Bao Y (2013) Fruit fly optimization algorithm based fractional order fuzzy-pid controller for electronic throttle. Nonlinear Dyn 73(1–2):611–619

    MathSciNet  Google Scholar 

  14. Wang L, Zheng XL, Wang SY (2013) A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem. Knowl Based Syst 48(2):17–C23

    Google Scholar 

  15. Pan QK, Sang HY, Duan JH, Gao L (2014) An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl Based Syst 62(5):69–83

    Google Scholar 

  16. Wang L, Liu R, Liu S (2016) An effective and efficient fruit fly optimization algorithm with level probability policy and its applications. Knowl Based Syst 97(C):158–174

    Google Scholar 

  17. Shan D, Cao GH, Dong HJ (2013) LGMS-FOA: an improved fruit fly optimization algorithm for solving optimization problems. Math Probl Eng 2013(7):1256–1271

    MATH  Google Scholar 

  18. Xu F, Tao Y (2014) The improvement of fruit fly optimization algorithm. Int J Autom Comput 10(03):227–241

    Google Scholar 

  19. Wu L, Xiao W, Zhang L, Liu Q, Wang J (2016) An improved fruit fly optimization algorithm based on selecting evolutionary direction intelligently. Int J Comput Intell Syst 9(1):80–90

    Google Scholar 

  20. Xiao C, Hao K, Ding Y (2015) An improved fruit fly optimization algorithm inspired from cell communication mechanism. Math Probl Eng 2015:1–15

    Google Scholar 

  21. Yuan X, Dai X, Zhao J, He Q (2014) On a novel multi-swarm fruit fly optimization algorithm and its application. Appl Math Comput 233(3):260–271

    MathSciNet  MATH  Google Scholar 

  22. Wang L, Shi Y, Liu S (2015) An improved fruit fly optimization algorithm and its application to joint replenishment problems. Expert Syst Appl 42(9):4310–4323

    Google Scholar 

  23. Tian X, Jie LI, S. O. Aeronautics, N. P. University (2017) An improved fruit fly optimization algorithm and its application in aerodynamic optimization design. Acta Aeronaut Astronaut Sin 38(4)

  24. Du TS, Ke XT, Liao JG, Shen YJ (2017) DSLC-FOA: an improved fruit fly optimization algorithm application to structural engineering design optimization problems. Appl Math Model. S0307904X17305310

  25. Darvish A, Ebrahimzadeh A (2018) Improved fruit-fly optimization algorithm and its applications in antenna arrays synthesis. IEEE Trans Antennas Propag PP(99):1–1

    Google Scholar 

  26. Dorigo M, Di CG, Gambardella LM (1999) Ant algorithm for discrete optimization. Arti Life 5(2):137–172

    Google Scholar 

  27. Dorigo M, Gambardella LM (1997) Ant colony system: a cooperative learning approach to the traveling salesman problem. IEEE Trans Evolut Comput 1(1):53–66

    Google Scholar 

  28. Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of IEEE international conference on neural networks, vol 4, pp 1942–1948

  29. Kennedy J, Eberhart R (2002) Particle swarm optimization. In: Proceedings of IEEE international conference on neural networks, vol 4, pp 1942–1948

  30. Karaboga D, Basturk B (2007) A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. Kluwer, Dordrecht

    MATH  Google Scholar 

  31. Rashedi E, Nezamabadi-Pour H, Saryazdi S (2012) Gsa: a gravitational search algorithm. Inf Sci 4(6):390–395

    MATH  Google Scholar 

  32. Deb K (1997) GeneAS: a robust optimal design technique for mechanical component design. Springer, Berlin

    Google Scholar 

  33. He Q, Wang L (2007) An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Eng Appl Artif Intell 20(1):89–99

    Google Scholar 

  34. Sandgren E (1990) Nonlinear integer and discrete programming in mechanical design. J Mech Des 112(2):223–229

    Google Scholar 

  35. Zhang C, Wang H-PB (1993) Mixed-discrete nonlinear optimization with simulated annealing. Eng Optim 21(4):277–291

    Google Scholar 

  36. Kannan BK, Kramer SN (1994) An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J Mech Des 116(2):405–411

    Google Scholar 

  37. Coello CAC (2000) Use of a self-adaptive penalty approach for engineering optimization problems. Comput Ind 41(2):113–127

    Google Scholar 

  38. Hu X, Eberhart RC, Shi Y (2003) Engineering optimization with particle swarm. In: Swarm intelligence symposium

  39. Gandomi AH, Yang X, Alavi AH (2013) Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng Comput 29(1):17–35

    Google Scholar 

  40. Lee KS, Geem ZW (2005) A new meta-heuristic algorithm for continuous engineering optimization: harmony search theory and practice. Comput Methods Appl Mech Eng 194(3638):3902–3933

    MATH  Google Scholar 

  41. Mezuramontes E, Coello CAC, Velazquezreyes J, Munozdavila L (2007) Multiple trial vectors in differential evolution for engineering design. Eng Optim 39(5):567–589

    MathSciNet  Google Scholar 

  42. Mezuramontes E, Coello CAC (2008) An empirical study about the usefulness of evolution strategies to solve constrained optimization problems. Int J Gen Syst 37(4):443–473

    MathSciNet  MATH  Google Scholar 

  43. Cagnina L, Esquivel SC, Coello CAC (2008) Solving engineering optimization problems with the simple constrained particle swarm optimizer. Informatica (Lith Acad Sci) 32(3):319–326

    MATH  Google Scholar 

  44. Kaveh A, Talatahari S (2009) Engineering optimization with hybrid particle swarm and ant colony optimization. Asian J Civ Eng (Build Hous) 10(6):611–628

    Google Scholar 

  45. Kaveh A, Talatahari S (2010) An improved ant colony optimization for constrained engineering design problems. Eng Comput 27(1):155–182

    MATH  Google Scholar 

  46. Coelho LDS (2010) Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems. Expert Syst Appl 37(2):1676–1683

    Google Scholar 

  47. Akay B, Karaboga D (2012) Artificial bee colony algorithm for large-scale problems and engineering design optimization. J Intell Manuf 23(4):1001–1014

    Google Scholar 

  48. Mazhoud I, Hadjhamou K, Bigeon J, Joyeux P (2013) Particle swarm optimization for solving engineering problems: a new constraint-handling mechanism. Eng Appl Artif Intell 26(4):1263–1273

    Google Scholar 

  49. Long W, Liang X, Huang Y, Chen Y (2014) An effective hybrid cuckoo search algorithm for constrained global optimization. Neural Comput Appl 25(3):911–926

    Google Scholar 

  50. Liu J, Wu C, Wu G, Wang X (2015) A novel differential search algorithm and applications for structure design. Appl Math Comput 268:246–269

    MATH  Google Scholar 

Download references

Acknowledgements

This study is supported by National Nature Science Foundation of China (Grant No. 41571016) and the National Key Research and Development Program of China (Grant No. 2018YFC0406606). The authors like to thank Prof. Yujing Lu, an English professor of Lanzhou University, for her proofreading. The authors are also thankful to anonymous referees for the valuable and constructive suggestions.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Lanzhou University, No. 222, TianShui Road (South), ChengGuan District, Lanzhou City, 730000, Gansu Province, China

    Xuan Yang, Weide Li, Lili Su, Yaling Wang & Ailing Yang

Authors
  1. Xuan Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Weide Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Lili Su
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yaling Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Ailing Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Weide Li.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, X., Li, W., Su, L. et al. An improved evolution fruit fly optimization algorithm and its application. Neural Comput & Applic 32, 9897–9914 (2020). https://doi.org/10.1007/s00521-019-04512-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-019-04512-2

Keywords