Robust speed prediction of high-speed trains based on improved echo state networks

Abstract

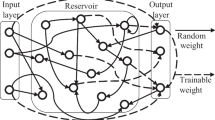
The accurate and robust speed prediction of high-speed trains (HSTs) is a challenging task in the automatic train operation (ATO) because HSTs operate in an open-air situation with much noise and many uncertainties. This paper contributes to the development of robust speed prediction methods for the ATO of HSTs based on improved echo state networks (ESNs). Firstly, an adaptive temporal scale selection approach is introduced to improve the accuracy and efficiency of ESN modeling, due to the importance of proper temporal scale selection in relation to the sound prediction performance of ESNs. Also, a random weight scaling mechanism is employed to enhance the feasibility and robustness of the proposed method, as the learning ability of ESNs lies in the constrained random connection weights. Furthermore, several conditions for the stability of the closed-loop control system are given. Our experiment results demonstrate that the proposed method successfully achieves sound performance in terms of speed prediction accuracy, efficiency and robustness.

Appendix A

Proof

Suppose $\mathbf{{x}}(t) = [{x_1}(t),{x_2}(t), \ldots ,{x_n}(t)]$, ${\mathbf{{x}}^\mathrm{{o}}}(t) = [{x^o}_1(t),{x^o}_2(t), \ldots ,{x^o}_n(t)]$ are two solutions of the system defined in (33), ${x_i}(t) = \xi (t):[ - {t_d},0] \rightarrow \mathbf{{R}}$ and ${x_i}^ \circ (t) = \eta (t):[ - {t_d},0] \rightarrow \mathbf{{R}}$, $\mathrm{{i = 1,2,}}\ldots \mathrm{{,n}}$, where $\xi (t)$ and $\eta (t)$ denote two different initial conditions for the system. Besides, let $\gamma$ and $\sigma$ be two time measuring scales satisfying that $\gamma - \phi _1\sigma = t - k\tau$ and $\gamma - \phi _2\sigma = t-\mu \tau$ with $\phi _1, \phi _2 \in \mathbf{Z}$. According to Definition 1 and (33), we have

$$\begin{aligned} \begin{array}{l} {I^\alpha }{D^\alpha }\left( {{x_i}(t) - {x^ \circ }_i(t)} \right) = \left( {{\xi _i}(0) - {\eta _i}(0)} \right) \mathrm{{ + }}\frac{1}{{\Gamma (\alpha )}}\int _0^t {{{(t - \tau )}^{\alpha - 1}}} \\ \quad \left\{ {f\left( {\sum \limits _{h = 1}^{{P_r}} {\sum \limits _{k = 1}^{{T_s}} {{\lambda _1}\left( {w_{h,k}^{in}{z_{h,k}}(t - k\tau ) + {b_0}} \right) } } } \right. } \right. \mathrm{{ + }}\left. {\sum \limits _{l = 1}^L {{\lambda _2}{w_l}{{x}^ \circ }{{_{i,}}_l}(t - \mu \tau )} } \right) \\ \quad - f\left( {\sum \limits _{h = 1}^{{P_r}} {\sum \limits _{k = 1}^{{T_s}} {{\lambda _1}\left( {w_{h,k}^{in}{z_{h,k}}(t - k\tau ) + {b_0}} \right) } } } \right. \left. {\left. {\mathrm{{ + }}\sum \limits _{l = 1}^L {{\lambda _2}{w_l}{{x}_{i,}}_l(t - \mu \tau )} } \right) } \right\} \mathrm{{d}}\tau \end{array} \end{aligned}$$

(37)

Here, let us set $\alpha \in (0,1)$. Then, from Assumption 1, Definition 2 and the properties of fractional operators [41, 42], we have

$$\begin{aligned} \begin{array}{l} {{e}^{ - t}}\left| {{x_i}(t) - {x^ \circ }_i(t)} \right| \le {{e}^{ - t}}\left| {{\xi _i}(0) - {\eta _i}(0)} \right| \\ \quad \mathrm{{ + }}\sum \limits _{l = 1}^L {\left| {{\lambda _2}{w_l}} \right| \frac{1}{{\Gamma (\alpha )}}\int _0^t {{{(t - \gamma )}^{\alpha - 1}}} {\mathrm{{C}}_f}{{e}^{ - t}}\left| {{{x}_{i,l}}(t - \mu ) - {{x}^ \circ }_{i,l}(t - \mu )} \right| } {d_\tau } \end{array} \end{aligned}$$

(38)

where e is the system tracking error. Define $\theta = \gamma - {\phi _2}\sigma$, thus (38) can be rewritten as follows:

$$\begin{aligned} \begin{array}{l} {e^{ - t}}\left| {{x_i}(t) - {x^ \circ }_i(t)} \right| \le {e^{ - t}}\left| {{\xi _i}(0) - {\eta _i}(0)} \right| \\ + \sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| \frac{1}{{\Gamma (\alpha )}}\int _{ - \mu }^{t - \mu } {{{(t - \theta - \mu )}^{\alpha - 1}}} {e^{ - t}}\left| {{{x}_{i,l}}(\theta ) - {{x}^ \circ }_{i,l}(\theta )} \right| } {d_\theta } \end{array} \end{aligned}$$

(39)

Let $\beta = t - \theta - {\phi _2}\sigma$ and extend the integrals of (38), then (39) can be rewritten as

$$\begin{aligned} \begin{array}{l} {{e}^{ - t}}\left| {{x_i}(t) - {x^ \circ }_i(t)} \right| \le {{e}^{ - t}}\left| {{\xi _i}(0) - {\eta _i}(0)} \right| \\ + \sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{e}^{ - {\phi _2}\sigma }}\frac{1}{{\Gamma (\alpha )}}\left\{ {\int _{\mathrm{{t - }}{\phi _2}\sigma }^t {{{(\beta )}^{\alpha - 1}}} {{e}^{ - \beta }}{d_\beta }} \right\} } {\sup _{t \in ( - {\phi _2}\sigma ,0]}}\left( {{{e}^{ - t}}\left| {{\xi _i}(t) - {\eta _i}(t)} \right| } \right) \\ + \sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{e}^{ - {\phi _2}\sigma }}\frac{1}{{\Gamma (\alpha )}}\left\{ {\int _0^{t - {\phi _2}\sigma } {{{(\beta )}^{\alpha - 1}}} {{e}^{ - \beta }}{d_\beta }} \right\} } {\sup _{t \in (0,t - {\phi _2}\sigma ]}}\left( {{{e}^{ - t}}\left| {{{x}_{i,l}}(t) - {{x}^ \circ }_{i,l}(t)} \right| } \right) \end{array} \end{aligned}$$

(40)

From Euler’s gamma function,

$$\begin{aligned} \Gamma (\alpha ) = \int _0^\infty {{e^{ - t}}{t^{\alpha - 1}}{d_t}} \end{aligned}$$

(41)

then (40) can be rewritten as

$$\begin{aligned} \begin{array}{l} {{e}^{ - t}}\left| {{x_i}(t) - {x^ \circ }_i(t)} \right| \le {{e}^{ - t}}\left| {{\xi _i}(0) - {\eta _i}(0)} \right| \\ \begin{array}{*{20}{c}} &\mathrm{{ + }} \end{array}\sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{e}^{ - {\phi _2}\sigma }}{{\sup }_{t \in ( - {\phi _2}\sigma ,0]}}\left( {{{e}^{ - t}}\left| {{\xi _i}(t) - {\eta _i}(t)} \right| } \right) } \\ \begin{array}{*{20}{c}} &\mathrm{{ + }} \end{array}\sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{e}^{ - {\phi _2}\sigma }}{{\sup }_{t \in (0,t - {\phi _2}\sigma ]}}\left( {{{e}^{ - t}}\left| {{{x}_{l,i}}(t) - {{x}^ \circ }_{l,i}(t)} \right| } \right) } \end{array} \end{aligned}$$

(42)

Since ${e^{ - {\phi _2}\sigma }} \in (0,1]$, it derives from (42) that

$$\begin{aligned} \begin{array}{l} {{e}^{ - t}}\left| {{x_i}(t) - {x^ \circ }_i(t)} \right| \le {{e}^{ - t}}\left| {{\xi _i}(0) - {\eta _i}(0)} \right| \\ \begin{array}{*{20}{c}} &\mathrm{{ + }} \end{array}\sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{\sup }_{t \in ( - {\phi _2}\sigma ,0]}}\left( {{{e}^{ - t}}\left| {{\xi _i}(t) - {\eta _i}(t)} \right| } \right) }\\ \begin{array}{*{20}{c}} &\mathrm{{ + }} \end{array}\sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{\sup }_{t \in (0,t - {\phi _2}\sigma ]}}\left( {{{e}^{ - t}}\left| {{{x}_{l,i}}(t) - {{x}^ \circ }_{l,i}(t)} \right| } \right) } \end{array} \end{aligned}$$

(43)

It follows that

$$\begin{aligned} {\sup _{t \in (0,{t_s}]}}\left| {{x}(t) - {{x}^ \circ }(t)} \right| \le {\sup _t}\left| {{x}(t) - {{x}^ \circ }(t)} \right| , 0<{t_s} < t \end{aligned}$$

(44)

thus (43) can be rewritten as

$$\begin{aligned} \begin{array}{l} {e^{ - t}}\left| {{x_i}(t) - {x^ \circ }_i(t)} \right| \le {e^{ - t}}\left| {{\xi _i}(0) - {\eta _i}(0)} \right| \\ \quad + \sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{\sup }_{t \in ( - {\phi _2}\sigma ,0]}}\left( {{e^{ - t}}\left| {{\xi _i}(t) - {\eta _i}(t)} \right| } \right) } \\ \quad + \sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{\sup }_t}\left( {{e^{ - t}}\left| {{{x}_{l,i}}(t) - {{x}^ \circ }_{l,i}(t)} \right| } \right) } \end{array} \end{aligned}$$

(45)

Then, we have

$$\begin{aligned} \begin{array}{l} \left\| {\mathbf{{x}}(t) - {\mathbf{{x}}^ \circ }(t)} \right\| \mathrm{{ = }}\sum \limits _{i = 1}^n {{{\sup }_t}\left( {{e^{ - t}}\left| {{x_i}(t) - {x^ \circ }_i(t)} \right| } \right) } \\ \quad \le \sum \limits _{i = 1}^n {{{\sup }_{t \in ( - {\phi _2}\sigma ,0]}}\left( {{e^{ - t}}\left| {{\xi _i}(0) - {\eta _i}(0)} \right| } \right) }\\ \quad + \sum \limits _{i = 1}^n {\sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{\sup }_{t \in ( - {\phi _2}\sigma ,0]}}\left( {{e^{ - t}}\left| {{\xi _i}(t) - {\eta _i}(t)} \right| } \right) } } \\ \quad + \sum \limits _{i = 1}^n {\sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| {{\sup }_t}\left( {{e^{ - t}}\left| {{{x}_{l,i}}(t) - {{x}^ \circ }_{l,i}(t)} \right| } \right) } } \end{array} \end{aligned}$$

(46)

Subsequently, we can obtain

$$\begin{aligned} \begin{array}{l} \left\| {\mathbf{{x}}(t) - {\mathbf{{x}}^ \circ }(t)} \right\| \le \left\| {{\varvec{\xi }}(t) - {\varvec{\eta }}(t)} \right\| \begin{array}{*{20}{l}} { + \sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| \left\| {{\varvec{\xi }}(t) - {\varvec{\eta }}(t)} \right\| } } \end{array} \\ \qquad + \sum \limits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| \left\| {\mathbf{{x}}(t) - {\mathbf{{x}}^ \circ }(t)} \right\| } \end{array} \end{aligned}$$

(47)

Using (34), we get

$$\begin{aligned} \left\| {\mathbf{{x}}(t) - {\mathbf{{x}}^ \circ }(t)} \right\| \le \frac{{1\mathrm{{ + }}\sum \nolimits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| } }}{{1 - \sum \nolimits _{l = 1}^L {{\mathrm{{C}}_f}\left| {{\lambda _2}{w_l}} \right| } }}\left\| {{\varvec{\xi }}(t) - {\varvec{\eta }}(t)} \right\| \end{aligned}$$

(48)

Thus, for any $\varepsilon > 0$, there is

$$\begin{aligned} \delta \le \left( {\frac{{1 - \sum \nolimits _{l = 1}^L {{\mathrm{{C}}_\mathrm{{f}}}\left| {{\lambda _2}{w_l}} \right| } }}{{1\mathrm{{ + }}\sum \nolimits _{l = 1}^L {{\mathrm{{C}}_\mathrm{{f}}}\left| {{\lambda _2}{w_l}} \right| } }}} \right) \varepsilon \end{aligned}$$

(49)

such that if $\left\| {{\varvec{\xi }}(t) - {\varvec{\eta }}(t)} \right\| \le \delta$, then

$$\begin{aligned} \left\| {\mathbf{{x}}(t) - {\mathbf{{x}}^ \circ }(t)} \right\| \le \varepsilon \end{aligned}$$

(50)

holds. Therefore, according to Definition 3, the system is uniformly stable and it converges to the equilibrium point with arbitrary precision. The proof is finished.