Skip to main content

Advertisement

Springer Nature Link
Log in

Spatiotemporal dynamic of a coupled neutral-type neural network with time delay and diffusion

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

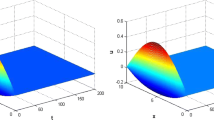
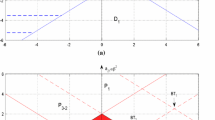
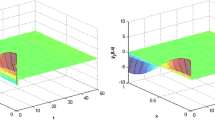
In this paper, a delayed neutral-type neural network with diffusion is considered. Three spatiotemporal dynamic problems of such network, i.e., stability, Turing instability and oscillation, are addressed in detail. It is found that the diffusion may lead to Turing instability, and the time delay may result in oscillation. Then, a novel computing method is proposed to investigate the oscillation properties. Finally, numerical results not only verify the obtained results but also show the diffusion coefficients have a great effect on the appearance of pattern. There are six spatiotemporal patterns when diffusion varying.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Shi P, Li F, Wu L (2017) Neural network-based passive filtering for delayed neutral-type semi-Markovian jump systems. IEEE Trans Neural Netw Lear Syst 28(9):2101–2114

    MathSciNet  Google Scholar 

  2. Van Hien L, Hai-An LD (2019) Positive solutions and exponential stability of positive equilibrium of inertial neural networks with multiple time-varying delays. Neural Comput Appl 31:6933–6943

    Article  Google Scholar 

  3. Wang P, Cheng J, Hao F (2020) Embedded adaptive cross-modulation neural network for few-shot learning. Neural Comput Appl 32:5505–5515

    Article  Google Scholar 

  4. Dong T, Huang T (2019) Neural cryptography based on complex-valued neural network. IEEE Trans Neural Netw Lear Syst. https://doi.org/10.1109/TNNLS.2019.2955165

    Article  Google Scholar 

  5. Ali MS, Saravanan S (2016) Robust finite-time H, control for a class of uncertain switched neural networks of neutral-type with distributed time varying delays. Neurocomputing 177:454–468

    Article  Google Scholar 

  6. Xiong W, Shi Y, Cao J (2017) Stability analysis of two-dimensional neutral-type Cohen-CGrossberg BAM neural networks. Neural Comput Appl 28(4):703–716

    Article  Google Scholar 

  7. Liu M, Xu X, Zhang C (2014) Stability and global Hopf bifurcation for neutral BAM neural network. Neurocomputing 145:122–130

    Article  Google Scholar 

  8. Zeng X, Xiong Z, Wang C (2016) Hopf bifurcation for neutral-type neural network model with two delays. Appl Math Comput 282(C):17–31

    MathSciNet  MATH  Google Scholar 

  9. Senan S, Syed AM, Vadivel R (2017) Decentralized event-triggered synchronization of uncertain Markovian jumping neutral-type neural networks with mixed delays. Neural Netw 86:32–41

    Article  Google Scholar 

  10. Wang R, Liu H, Feng F (2017) Bogdanov–Takens bifurcation in a neutral BAM neural networks model with delays. Iet Syst Biol 11(6):163–173

    Article  Google Scholar 

  11. Dong T, Zhang Q (2020) Stability and oscillation analysis of a gene regulatory network with multiple time delays and diffusion rate. IEEE Trans NanoBioscience 19:285–298

    Article  Google Scholar 

  12. Ge J, Xu J, Li ZQ (2016) Zero-Hopf bifurcation and multistability coexistence on a four-neuron network model with multiple delays. Nonlinear Dyn 87(4):1–10

    MathSciNet  Google Scholar 

  13. Gao S, Zhou H, Wu B (2017) Periodic solutions for neutral coupled oscillators network with feedback and time-varying delay. Appl Anal 96(12):1983–2001

    Article  MathSciNet  Google Scholar 

  14. Huang C, Cao J (2018) Impact of leakage delay on bifurcation in high-order fractional BAM neural networks. Neural Netw 98:223–235

    Article  Google Scholar 

  15. Song X, Wang M, Song S (2019) Intermittent pinning synchronization of reaction–diffusion neural networks with multiple spatial diffusion couplings. Neural Comput Applic 31:9279–9294

    Article  Google Scholar 

  16. Dong T, Bai J, Yang L (2019) Bifurcation analysis of delayed complex-valued neural network with diffusions. Neural Process Lett 50:1019–1033

    Article  Google Scholar 

  17. Liang X, Wang L, Wang Y (2016) Dynamical behavior of delayed reaction diffusion Hopfield neural networks driven by infinite dimensional Wiener processes. IEEE Trans Neural Netw Learn Syst 27(9):1816–1826

    Article  MathSciNet  Google Scholar 

  18. Meng L, Li X, Zhang G (2017) Simple diffusion can support the pitchfork, the flip bifurcations, and the chaos. Commun Nonlinear Sci Numer Simul 53:202–212

    Article  MathSciNet  Google Scholar 

  19. Dong T, Xu W, Liao X (2017) Hopf bifurcation analysis of reaction-Cdiffusion neural oscillator system with excitatory-to-inhibitory connection and time delay. Nonlinear Dyn 89(4):2329–2345

    Article  Google Scholar 

  20. Sheng Y, Zeng Z (2017) Synchronization of stochastic reaction diffusion neural networks with Dirichlet boundary conditions and unbounded delays. Neural Netw 93:89–98

    Article  Google Scholar 

  21. Dong T, Xia L (2019) Spatial temporal dynamic of a coupled reaction-diffusion neural network with time delay. Cogn Comput 11:212–226

    Article  Google Scholar 

  22. Liu X, Chen Z, Zhou L (2017) Synchronization of coupled reaction diffusion neural networks with hybrid coupling via aperiodically intermittent pinning control. J Frankl Inst 354(15):7053–7076

    Article  MathSciNet  Google Scholar 

  23. Wei T, Wang L, Wang Y (2017) Existence, uniqueness and stability of mild solutions to stochastic reaction-Cdiffusion Cohen-CGrossberg neural networks with delays and wiener processes. Neurocomputing 239:19–27

    Article  Google Scholar 

  24. Dong Y, Guo L, Hao J (2020) Robust exponential stabilization foruncertain neutral neural networks with interval time-varying delaysby periodically intermittent control. Neural Comput Appl 32:2651–C2664

    Article  Google Scholar 

  25. Dong T, Xia L (2017) Stability and Hopf Bifurcation of a reaction diffusion neutral neuron system with time delay. Int J Bifurc Chaos 27(14):1750214

    Article  MathSciNet  Google Scholar 

  26. Wei X, Wei J (2017) Turing instability and bifurcation analysis in a diffusive bimolecular system with delayed feedback. Commun Nonlinear Sci Numer Simul 50:241–255

    Article  MathSciNet  Google Scholar 

  27. Dong T, Hu W, Liao X (2016) Dynamics of the congestion control model in underwater wireless sensor networks with time delay. Chaos Solitons Fractals 92:130–136

    Article  Google Scholar 

  28. Liu Q, Liao X, Liu Y et al (2009) Dynamics of an inertial two-neuron system with time delay. Nonlinear Dyn 58(3):573

    Article  MathSciNet  Google Scholar 

  29. Yu W, Cao J (2005) Hopf bifurcation and stability of periodic solutions for van der Pol equation with time delay. Nonlinear Anal. Theory Methods Appl 62(1):141–165

    Article  MathSciNet  Google Scholar 

  30. Wu J (2012) Theory and applications of partial functional differential equations. Springer Science & Business Media, Berlin

    Google Scholar 

  31. Wang C (2020) Normal forms for partial neutral functional differential equations with applications to diffusive lossless transmission line. Int J Bifurc Chaos 30(2):2050028

    Article  MathSciNet  Google Scholar 

  32. Wang C, Wei J (2019) Hopf Bifurcations for Neutral Functional Differential Equations with Infinite Delays. Funkc ekvacioj-serio internacia 62(1):95–127

    Article  MathSciNet  Google Scholar 

  33. Wang C, Wei J (2010) Hopf bifurcation for neutral functional differential equations. Nonlinear Anal Real World Appl 11:1269–1277

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Key Research and Development Project of China under Grant 2018AAA0100101, in part by Chongqing Social Science Planning Project under Grant 2019BS053, in part by Fundamental Research Funds for the Central Universities under Grant XDJK2020B009, in part by the Chongqing Technological Innovation and Application Project under Grant cstc2018jszx-cyzdX0171, in part by Chongqing Basic and Frontier Research Project under Grant cstc2019jcyj-msxm2105, in part by the Science and Technology Research Program of Chongqing Municipal Education Commission under Grant KJQN201900816.

Author information

Authors and Affiliations

  1. Research Center for Enterprise Management, School of Business Administration, Chongqing Technology and Business University, Chongqing, 400067, People’s Republic of China

    Wenjie Hu

  2. Chongqing Key Laboratory of Nonlinear Circuits and Intelligent Information Processing, College of Electronics and Information Engineering, Southwest University, Chongqing, 400715, People’s Republic of China

    Wenjie Hu, Xing Qiao & Tao Dong

Authors
  1. Wenjie Hu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xing Qiao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Tao Dong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Tao Dong.

Ethics declarations

Conflicts of interest

The authors declared that they have no conflicts of interest to this work. We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hu, W., Qiao, X. & Dong, T. Spatiotemporal dynamic of a coupled neutral-type neural network with time delay and diffusion. Neural Comput & Applic 33, 6415–6426 (2021). https://doi.org/10.1007/s00521-020-05404-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-020-05404-6

Keywords