Skip to main content

Advertisement

Springer Nature Link
Log in

Soil–conduit interaction: an artificial intelligence application for reinforced concrete and corrugated steel conduits

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

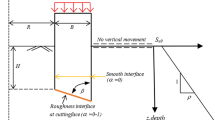
Marston’s load theory is commonly used for understanding the soil–conduit interaction. However, there are no practical methods available which can estimate the Marston’s soil prism (MSP) width ratio. Moreover, the advent of soft computing methods has made many traditional approaches antiquated. The main purpose of this work is to compare and evaluate the predictive abilities of several machine learning-based models in predicting the MSP width ratio for the reinforced concrete (RC) and corrugated steel (CS) conduits. By utilizing the finite element modelling, a large-scale dataset was generated for the width of the soil prism for both types of conduit material, when buried under sandy soils of varying stiffness. After preparing the required dataset, feature validity technique based on correlation-based feature selection was employed to find the most influential parameters affecting the MSP width. Thereafter, five regression-based data driven models namely artificial neural networks (ANN), least-square support vector regression, extreme learning machine, Gaussian process regression, and multiple linear regression were developed to forecast the MSP width ratio. The results showed that the ANN outperforms the other predictive models for both the conduit types. In addition, due to the excellent overall performance of the ANN, it was translated into functional relationship for predicting the MSP width ratio for RC and CS conduits.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Watkins RK, Anderson LR (1999) Structural mechanics of buried pipes. CRC Press, Boca Raton

    Book  Google Scholar 

  2. Khan MUA, Shukla SK (2020) Load-settlement response and bearing capacity of a surface footing located over a conduit buried within a soil slope. Int J Geomech 20(10):04020173

    Article  Google Scholar 

  3. Marston MG (1930) The theory of external loads on closed conduits in the light of the latest experiments. Proc Highw Res Board 9:138–170

    Google Scholar 

  4. White LH, Layer PJ (1960) The corrugated metal conduit as a compression ring. Proc Highw Res Board 39:389–397

    Google Scholar 

  5. Burghignoli A (1981) Soil interaction in buried structures. Proc Int Conf Soil Mech Found Eng 1519:69–74

    Google Scholar 

  6. Spangler MG (1962) Culverts and conduits. McGraw Hill, New York

    Google Scholar 

  7. Whitman RV, Luscher U (1962) Basic experiment into soil–structure interaction. J Soil Mech Found Div 88(6):135–168

    Article  Google Scholar 

  8. Finn WD (1963) Boundary value problems of soil mechanics. J Soil Mech Found Div 89(5):39–72

    Article  Google Scholar 

  9. Chelapati CV (1964) Arching in soil due to the deflection of a rigid horizontal strip. In: Proceedings of the symposium on soil-structure interaction, pp 356–377

  10. Nielson FD (1966) Soil-structure-arching analysis of buried flexible structures. Ph.D. Dissertation, University of Arizona

  11. Bjerrum LC, Frimann LJ, Has M, Duncan JM (1972) Earth pressures on flexible structures—a state of the art report. In: Proceedings, fifth european conference on soil mechanics and foundation engineering, pp 169–196

  12. Selig ET (1990) Soil properties for plastic pipe installations. ASTM Spec Tech Publ, pp 141–158

  13. Khan MUA, Shukla SK (2021) Vertical load on a conduit buried under a sloping ground. Geomech Eng Int J 24(6):599–610. https://doi.org/10.12989/gae.2021.24.6.599

    Article  Google Scholar 

  14. Marston A, Anderson AO (1913) The theory of loads on pipe in ditches and tests of cement and clay drain tile and sewer pipe. Iowa State Coll Agric Mech Arts 31:1–185

    Google Scholar 

  15. Terzaghi K (1943) Theoretical soil mechanics. Wiley, New York

    Book  Google Scholar 

  16. Moser AP, Folkman SL (2001) Buried pipe design. McGraw-Hill, New York

    Google Scholar 

  17. Greenwood ME, Lang DC (1990) Vertical deflection of buried flexible pipes. ASTM Spec Tech Publ, pp 185–214

  18. Moore ID (2001) Buried pipes and culverts. In: Geotechnical and geoenvironmental engineering handbook, pp 541–567

  19. Kang J, Parker F, Kang YJ, Yoo CH (2008) Effects of frictional forces acting on sidewalls of buried box culverts. Int J Numer Anal Methods Geomech 32(3):289–306

    Article  MATH  Google Scholar 

  20. Kim MK, Cho SH, Yun IJ, Won JH (2012) Three-dimensional responses of buried corrugated pipes and ANN-based method for predicting pipe deflections. Int J Numer Anal Methods Geomech 36(1):1–16

    Article  Google Scholar 

  21. Vu-Bac N, Lahmer T, Zhuang X, Nguyen-Thoi T, Rabzuk T (2016) A software framework for probabilistic sensitivity analysis for computationally expensive models. Adv Eng Softw 100:19–31

    Article  Google Scholar 

  22. Acharyya R, Dey A (2019) Assessment of bearing capacity for strip footing located near sloping surface considering ANN model. Neural Comput Appl 31:8087–8100

    Article  Google Scholar 

  23. Kardani N, Zhou A, Nazem M, Shen SL (2021) Improved prediction of slope stability using a hybrid stacking ensemble method based on finite element analysis and field data. J Rock Mech Geotech Eng 13(1):188-201

    Article  Google Scholar 

  24. Zhang K, Lyu HM, Shen SL, Zhou A, Yin ZY (2020) Evolutionary hybrid neural network approach to predict shield tunneling-induced ground settlements. Tunn Undergr Sp Technol 106:103594

    Article  Google Scholar 

  25. Moayedi H, Hayati S (2018) Modelling and optimization of ultimate bearing capacity of strip footing near a slope by soft computing methods. Appl Soft Comput J 66:208–219

    Article  Google Scholar 

  26. Moayedi H, Moatamediyan A, Nguyen H, Bui XN, Bui DT, Rashid ASA (2020) Prediction of ultimate bearing capacity through various novel evolutionary and neural network models. Eng Comput 36:671–687

    Article  Google Scholar 

  27. Yuan C, Moayedi H (2020) Evaluation and comparison of the advanced metaheuristic and conventional machine learning methods for the prediction of landslide occurrence. Eng Comput 36:1801–1811

    Article  Google Scholar 

  28. Raja MNA, Shukla SK, Khan MUA (2021) An intelligent approach for predicting the strength of geosynthetic-reinforced subgrade soil. Int J Pavement Eng. https://doi.org/10.1080/10298436.2021.1904237

    Article  Google Scholar 

  29. Tarawneh B, Nusairat J, Hakam Y (2018) Load testing and settlement of shallow foundation on desert sands. Proc Inst Civ Eng Geotech Eng 171(1):52–63

    Article  Google Scholar 

  30. Shao Z, Jahed Armaghani D, Bejarbaneh BY, Muazu MA, Mohamad ET (2019) Estimating the friction angle of black shale core specimens with hybrid-ANN approaches. Meas J Int Meas Confed 145:744–755

    Article  Google Scholar 

  31. Raja MNA, Shukla SK (2021) Predicting the settlement of geosynthetic-reinforced soil foundations using evolutionary artificial intelligence technique. Geotext Geomembranes. https://doi.org/10.1016/j.geotexmem.2021.04.007

    Article  Google Scholar 

  32. Acharyya R, Dey A, Kumar B (2020) Finite element and ANN-based prediction of bearing capacity of square footing resting on the crest of c-φ soil slope. Int J Geotech Eng 14(2):176–187

    Article  Google Scholar 

  33. Gao W, Raftari M, Rashid ASA, Muazu MA, Jusoh WAW (2020) A predictive model based on an optimized ANN combined with ICA for predicting the stability of slopes. Eng Comput 36(1):325–344

    Article  Google Scholar 

  34. Tafreshi SNM, Mehrjardi GT (2008) The use of neural network to predict the behavior of small plastic pipes embedded in reinforced sand and surface settlement under repeated load. Eng Appl Artif Intell 21(6):883–894

    Article  Google Scholar 

  35. Shokouhi SKS, Dolatshah A, Ghobakhloo E (2013) Seismic strain analysis of buried pipelines in a fault zone using hybrid FEM-ANN approach. Earthq Struct 5(4):417–438

    Article  Google Scholar 

  36. Sargand SM, Masada T (2003) Soil arching over deeply buried thermoplastic pipe. Transp Res Rec 1849(1):109–118

    Article  Google Scholar 

  37. Qin X, Ni P, Zhou M (2017) Improved analytical solution of vertical pressure on top of induced trench rigid culverts. Geosynth Int 24(6):615–624

    Article  Google Scholar 

  38. Fan CC, Luo JH (2008) Numerical study on the optimum layout of soil-nailed slopes. Comput Geotech 35(4):585–599

    Article  Google Scholar 

  39. Ghazavi M, Eghbali AH (2008) A simple limit equilibrium approach for calculation of ultimate bearing capacity of shallow foundations on two-layered granular soils. Geotech Geol Eng 26:535–542

    Article  Google Scholar 

  40. Brinkgreve RB, Kumarswamy S, Swolfs WM, Foria F (2018) Plaxis 2D technical manual. Rotterdam, London

    Google Scholar 

  41. Elshimi TM, Moore ID (2013) Modeling the effects of backfilling and soil compaction beside shallow buried pipes. J Pipeline Syst Eng Pract 4(4):04013004

    Article  Google Scholar 

  42. Wadi A, Pettersson L, Karoumi R (2015) Flexible culverts in sloping terrain: numerical simulation of soil loading effects. Eng Struct 101:111–124

    Article  Google Scholar 

  43. Sharma V, Kumar A (2018) Behavior of ring footing resting on reinforced sand subjected to eccentric-inclined loading. J Rock Mech Geotech Eng 10:347–357

    Article  Google Scholar 

  44. Mcgrath TJ (1998) Calculating loads on buried culverts based on pipe hoop stiffness. Transp Res Rec 1656(1):73–79

    Article  Google Scholar 

  45. Gao W, Alsarraf J, Moayedi H, Shahsavar A, Nguyen H (2019) Comprehensive preference learning and feature validity for designing energy-efficient residential buildings using machine learning paradigms. Appl Soft Comput J 84:105748

    Article  Google Scholar 

  46. Cai J, Luo J, Wang S, Yang S (2018) Feature selection in machine learning: a new perspective. Neurocomputing 300:70–79

    Article  Google Scholar 

  47. Guyon I, Elisseeff A (2003) An introduction to variable and feature selection. J Mach Learn Res 3:1157–1182

    MATH  Google Scholar 

  48. Shahin MA, Maier HR, Jaksa MB (2002) Predicting settlement of shallow foundations using neural networks. J Geotech Geoenvironmental Eng 128:785–793

    Article  Google Scholar 

  49. Samui P, Sitharam TG (2008) Least-square support vector machine applied to settlement of shallow foundations on cohesionless soils. Int J Numer Anal Methods Geomech 32:2033–2043

    Article  MATH  Google Scholar 

  50. Pal M, Deswal S (2010) Modelling pile capacity using Gaussian process regression. Comput Geotech 37:942–947

    Article  Google Scholar 

  51. Samui P, Kim D (2013) Least square support vector machine and multivariate adaptive regression spline for modeling lateral load capacity of piles. Neural Comput Appl 23:1123–1127

    Article  Google Scholar 

  52. Liu Z, Shao J, Xu W, Wu Q (2015) Indirect estimation of unconfined compressive strength of carbonate rocks using extreme learning machine. Acta Geotech 10:651–663

    Article  Google Scholar 

  53. Suthar M (2020) Applying several machine learning approaches for prediction of unconfined compressive strength of stabilized pond ashes. Neural Comput Appl 32:9019–9028

    Article  Google Scholar 

  54. Raja MNA, Shukla SK (2020) An extreme learning machine model for geosynthetic-reinforced sandy soil foundations. Proc Inst Civ Eng Geotech Eng. https://doi.org/10.1680/jgeen.19.00297

    Article  Google Scholar 

  55. Bishop CM (1995) Neural networks for pattern recognition. Oxford University Press, Oxford

    MATH  Google Scholar 

  56. Witten IH, Frank E, Hall MA, Pal CJ (2016) Data mining: practical machine learning tools and techniques. Morgan Kaufmann, Cambridge

    Google Scholar 

  57. Rumelhart DE (1986) Parallel distributed processing: explorations in the microstructure of cognition. In: Learning internal representations by error propagation. MIT press, Cambridge, pp 318–362

  58. Goh ATC (1995) Back-propagation neural networks for modeling complex systems. Artif Intell Eng 9(3):143–151

    Article  Google Scholar 

  59. Ashrafian A, Shokri F, Taheri Amiri MJ, Yaseen ZM, Rezaie-Balf M (2020) Compressive strength of foamed cellular lightweight concrete simulation: new development of hybrid artificial intelligence model. Constr Build Mater 230:117048

    Article  Google Scholar 

  60. Zurada JM (1992) Introduction to artificial neural systems. West Publishing Company, St. Paul

    Google Scholar 

  61. Haykin S (1994) Neural networks: a comprehensive foundation. Macmillan College Publishing Company, Englewood Cliffs

    MATH  Google Scholar 

  62. Cherkassky V, Mulier FM (2007) Learning from data: concepts, theory, and methods. John Wiley & Sons, New York

    Book  MATH  Google Scholar 

  63. Xue X, Yang X (2016) Seismic liquefaction potential assessed by support vector machines approaches. Bull Eng Geol Environ 75(1):153–162

    Article  Google Scholar 

  64. Zhao H, Ru Z, Yin S (2015) A practical indirect back analysis approach for geomechanical parameters identification. Mar Georesour Geotechnol 33(3):212–221

    Article  Google Scholar 

  65. Zhuang DY, Ma K, Tang CA, Liang ZZ, Wang KK, Wang ZW (2019) Mechanical parameter inversion in tunnel engineering using support vector regression optimized by multi-strategy artificial fish swarm algorithm. Tunn Undergr Sp Technol 83:425–436

    Article  Google Scholar 

  66. Cortes C, Vapnik V (1995) Support-vector networks. Mach Learn 20(3):273–297

    Article  MATH  Google Scholar 

  67. Cristianini N, Shawe-Taylor JS-TJ (2000) An introduction to support vector machines and other kernel-based learning methods. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  68. Chang CC, Lin CJ (2001) LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol 2(3):1–27

    Article  Google Scholar 

  69. Vapnik V (1995) The nature of statistical learning theory. Springer, New York

    Book  MATH  Google Scholar 

  70. Suykens JAK, Vandewalle J (1999) Least squares support vector machine classifiers. Neural Process Lett 9(3):293–300

    Article  Google Scholar 

  71. Kisi O (2015) Pan evaporation modeling using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J Hydrol 528:312–320

    Article  Google Scholar 

  72. Samui P (2008) Slope stability analysis: a support vector machine approach. Environ Geol 56(2):255–267

    Article  Google Scholar 

  73. Mercer J (1909) Functions of positive and negative type and their connection with the theory of integral equations. Philos Trans R Soc 209:441–458

    MATH  Google Scholar 

  74. Bin HG, Chen L, Siew CK (2006) Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Trans Neural Netw 17(4):879–892

    Article  Google Scholar 

  75. Ding S, Zhao H, Zhang Y, Xu X, Nie R (2015) Extreme learning machine: algorithm, theory and applications. Artif Intell Rev 44(1):103–115

    Article  Google Scholar 

  76. Rasmussen CEWC (2006) Gaussian processes for machine learning. MIT press, Cambridge

    MATH  Google Scholar 

  77. Sobhani J, Najimi M, Pourkhorshidi AR, Parhizkar T (2010) Prediction of the compressive strength of no-slump concrete: a comparative study of regression, neural network and ANFIS models. Constr Build Mater 24(5):709–718

    Article  Google Scholar 

  78. Kumar S, Basudhar PK (2018) A neural network model for slope stability computations. Geotech Lett 8(2):149–154

    Article  Google Scholar 

  79. Stone M (1974) Cross-validatory choice and assessment of statistical predictions. J R Stat Soc Ser B 36(2):111–113

    MathSciNet  MATH  Google Scholar 

  80. Soleimanbeigi A, Hataf N (2006) Prediction of settlement of shallow foundations on reinforced soils using neural networks. Geosynth Int 13(4):161–170

    Article  Google Scholar 

  81. Das SK, Sivakugan N (2010) Discussion of “intelligent computing for modeling axial capacity of pile foundations.” Can Geotech J 47(8):928–930

    Article  Google Scholar 

  82. Ranganathan A (2004) The Levenberg–Marquardt algorithm. Tutor LM Algorithm 11(1):101–110

    Google Scholar 

  83. Hornik K, Stinchcombe M, White H (1989) Multilayer feedforward networks are universal approximators. Neural Netw 2:359–366

    Article  MATH  Google Scholar 

  84. Aamir M, Tolouei-Rad M, Vafadar A, Raja MNA, Giasin K (2020) Performance analysis of multi-spindle drilling of Al2024 with TiN and TiCN coated drills using experimental and artificial neural networks technique. Appl Sci 10(23):8633

    Article  Google Scholar 

  85. Yaseen ZM, Deo RC, Hilal A et al (2018) Predicting compressive strength of lightweight foamed concrete using extreme learning machine model. Adv Eng Softw 115:112–125

    Article  Google Scholar 

  86. Deo RC, Kisi O, Singh VP (2017) Drought forecasting in eastern Australia using multivariate adaptive regression spline, least square support vector machine and M5Tree model. Atmos Res 184:149–175

    Article  Google Scholar 

  87. Raja MNA, Shukla SK (2021) Multivariate adaptive regression splines model for reinforced soil foundations. Geosynth Int. https://doi.org/10.1680/jgein.20.00049

    Article  Google Scholar 

  88. Montgomery DC, Peck EA, Vining GG (2012) Introduction to linear regression analysis. Wiley, New York

    MATH  Google Scholar 

  89. Alsharari B, Olenko A, Abuel-Naga H (2020) Modeling of electrical resistivity of soil based on geotechnical properties. Expert Syst Appl 141:112966

    Article  Google Scholar 

Download references

Acknowledgements

This research was funded by The Higher Education Commission (HEC), Government of the Islamic Republic of Pakistan. The authors also acknowledge the assistance provided by Mrs. Saman Tariq in the extraction of images.

Author information

Authors and Affiliations

  1. Geotechnical and Geoenvironmental Research Group, School of Engineering, Edith Cowan University, Joondalup, Perth, WA, 6027, Australia

    Muhammad Umer Arif Khan, Sanjay Kumar Shukla & Muhammad Nouman Amjad Raja

  2. Department of Civil Engineering, Mirpur University of Science and Technology, Mirpur, Azad Kashmir, Pakistan

    Muhammad Umer Arif Khan

  3. Delhi Technological University, New Delhi, Delhi, India

    Sanjay Kumar Shukla

  4. Department of Civil Engineering, School of Engineering, University of Management and Technology, Lahore, Pakistan

    Muhammad Nouman Amjad Raja

Authors
  1. Muhammad Umer Arif Khan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Sanjay Kumar Shukla
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Muhammad Nouman Amjad Raja
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Muhammad Umer Arif Khan.

Ethics declarations

Conflict of interest

Authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Weights and biases of the developed ANN models

Appendix: Weights and biases of the developed ANN models

1.1 RC conduit

Synaptic weights between the input and hidden layer (w1)

− 3.560

− 1.221

− 0.311

− 1.025

2.413

− 0.150

− 0.079

0.092

3.147

− 4.639

− 1.221

− 0.284

− 0.803

2.180

− 0.120

− 0.067

0.058

4.700

− 0.100

− 0.911

1.105

− 2.060

5.311

− 0.506

0.296

− 1.580

− 1.990

20.407

− 1.206

6.340

0.643

− 1.139

− 1.071

0.377

0.609

0.544

− 9.947

− 0.184

− 0.074

0.144

0.054

0.124

− 0.009

− 0.101

− 0.049

− 1.842

− 1.970

1.147

− 0.719

2.939

− 3.538

− 1.705

− 0.224

0.553

0.235

− 0.568

0.083

0.342

− 0.242

− 0.836

− 0.080

0.572

− 1.578

− 12.409

2.338

0.635

− 0.365

− 1.234

− 1.652

− 0.156

1.261

2.186

− 0.233

0.791

0.020

− 0.219

− 0.181

1.063

0.098

− 0.713

1.591

− 4.059

− 0.860

− 0.565

− 2.186

2.776

1.090

0.118

− 0.829

0.159

Synaptic weights between the hidden and output layer (w2)

− 3.394

3.108

− 0.256

− 7.023

− 7.439

0.018

2.472

0.484

2.270

0.539

Bias of hidden layer nodes (b1)

− 5.28921

− 7.15092

− 6.14941

− 0.31111

− 1.94642

− 3.0193

− 1.84741

− 10.2446

2.049577

− 4.14727

Bias of output layer node (b2)

− 0.6967.

1.2 CS conduit

Synaptic weights between the input and hidden layer (\(w_{1}\))

− 0.207

0.054

− 0.603

0.018

0.252

− 0.915

− 0.130

1.014

2.958

5.606

3.056

− 5.208

− 0.321

− 0.889

− 0.039

− 2.008

3.869

− 7.328

0.500

0.064

− 0.059

− 0.040

− 0.183

0.002

0.140

0.223

− 0.135

0.504

− 0.521

− 0.847

− 0.046

1.410

0.134

0.045

0.021

− 0.160

− 1.343

− 2.779

3.820

1.191

− 0.034

− 0.718

− 1.655

0.676

− 16.225

− 1.359

− 2.700

4.137

1.244

− 0.432

− 0.536

− 1.670

0.417

− 16.105

0.478

0.437

0.869

0.239

0.105

− 1.274

− 0.454

1.002

1.169

0.123

− 0.669

− 0.077

0.089

0.985

0.764

0.102

− 0.892

− 2.952

0.240

0.753

− 4.565

− 1.360

− 2.116

0.139

− 2.581

0.539

1.198

0.265

− 0.255

− 0.404

− 0.041

0.866

0.106

− 0.039

− 0.078

− 0.118

Synaptic weights between the hidden and output layer (w2)

− 0.990

0.639

− 0.795

1.328

4.689

− 4.602

− 0.018

− 1.113

− 0.027

− 3.244

Bias of hidden layer nodes (b1)

0.398

− 15.068

0.788

0.585

− 3.925

− 4.069

− 1.588

− 0.493

− 3.986

1.202

Bias of output layer node (b2)

2216

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khan, M.U.A., Shukla, S.K. & Raja, M.N.A. Soil–conduit interaction: an artificial intelligence application for reinforced concrete and corrugated steel conduits. Neural Comput & Applic 33, 14861–14885 (2021). https://doi.org/10.1007/s00521-021-06125-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-021-06125-0

Keywords