Skip to main content

Advertisement

Springer Nature Link
Log in

Multistability and circuit implementation of tabu learning two-neuron model: application to secure biomedical images in IoMT

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

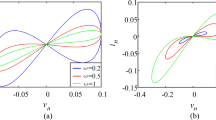
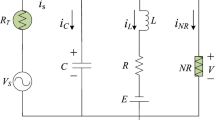
In this paper, the dynamics of a non-autonomous tabu learning two-neuron model is investigated. The model is obtained by building a tabu learning two-neuron (TLTN) model with a composite hyperbolic tangent function consisting of three hyperbolic tangent functions with different offsets. The possibility to adjust the compound activation function is exploited to report the sensitivity of non-trivial equilibrium points with respect to the parameters. Analysis tools like bifurcation diagram, Lyapunov exponents, phase portraits, and basin of attraction are used to explore various windows in which the neuron model under the consideration displays the uncovered phenomenon of the coexistence of up to six disconnected stable states for the same set of system parameters in a TLTN. In addition to the multistability, nonlinear phenomena such as period-doubling bifurcation, hysteretic dynamics, and parallel bifurcation branches are found when the control parameter is tuned. The analog circuit is built in PSPICE environment, and simulations are performed to validate the obtained results as well as the correctness of the numerical methods. Finally, an encryption/decryption algorithm is designed based on a modified Julia set and confusion–diffusion operations with the sequences of the proposed TLTN model. The security performances of the built cryptosystem are analyzed in terms of computational time (CT = 1.82), encryption throughput (ET = 151.82 MBps), number of cycles (NC = 15.80), NPCR = 99.6256, UACI = 33.6512, χ2-values = 243.7786, global entropy = 7.9992, and local entropy = 7.9083. Note that the presented values are the optimal results. These results demonstrate that the algorithm is highly secured compared to some fastest neuron chaos-based cryptosystems and is suitable for a sensitive field like IoMT security.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Beyer D, Ogier RG (1991) Tabu learning: a neural network search method for solving nonconvex optimization problems. In: [Proceedings] 1991 IEEE International Joint Conference on Neural Networks, pp 953–961. IEEE

  2. Glover F (1990) Tabu search—part II. ORSA J Comput 2(1):4–32

    Article  MATH  Google Scholar 

  3. Glover F (1989) Tabu search—part I. ORSA J Comput 1(3):190–206

    Article  MATH  Google Scholar 

  4. Li C, Chen G, Liao X (2005) Yu, J, Chaos: Hopf bifurcation and chaos in tabu learning neuron models. Int. J. Bifurcation Chaos 15(08):2633–2642

    Article  MATH  Google Scholar 

  5. Zhou X, Wu Y, Li Y, Ye Y (2006) Hopf bifurcation analysis on a tabu learning single neuron model in the frequency domain. In: 2006 International Conference on Communications, Circuits and Systems 2006, pp 2042–2045. IEEE

  6. Xiao M, Cao J (2008) Bifurcation analysis on a discrete-time tabu learning model. J Comput Appl Math 220(1–2):725–738

    Article  MathSciNet  MATH  Google Scholar 

  7. Jun C, Chun-Guang L (2011) Circuit design of tabu learning neuron models and their dynamic behavior. Acta Phys Sin 60(2):020502

    Article  Google Scholar 

  8. Li Y (2011) Hopf bifurcation analysis in a tabu learning neuron model with two delays. ISRN Appl Math. https://doi.org/10.5402/2011/636732

    Article  MathSciNet  MATH  Google Scholar 

  9. Bao B, Hou L, Zhu Y, Wu H, Chen M (2020) Bifurcation analysis and circuit implementation for a tabu learning neuron model. AEU Int J Electron Commun 121:153235

    Article  Google Scholar 

  10. Zhu D, Hou L, Chen M, Bao B (2020) FPGA-based experiments for demonstrating bi-stability in tabu learning neuron model. Circuit World. https://doi.org/10.1108/CW-12-2019-0189

    Article  Google Scholar 

  11. Bao B, Chen C, Bao H, Zhang X, Xu Q, Chen M (2019) Dynamical effects of neuron activation gradient on Hopfield neural network: numerical analyses and hardware experiments. Int J Bifur Chaos 29(04):1930010

    Article  MathSciNet  MATH  Google Scholar 

  12. Bao B, Qian H, Wang J, Xu Q, Chen M, Wu H, Yu Y (2017) Numerical analyses and experimental validations of coexisting multiple attractors in Hopfield neural network. Nonlinear Dyn 90(4):2359–2369

    Article  MathSciNet  Google Scholar 

  13. Bao B, Qian H, Xu Q, Chen M, Wang J, Yu Y (2017) Coexisting behaviors of asymmetric attractors in hyperbolic-type memristor based Hopfield neural network. Front Comput Neurosci 11:81

    Article  Google Scholar 

  14. Chen C, Bao H, Chen M, Xu Q, Bao B (2019) Non-ideal memristor synapse-coupled bi-neuron Hopfield neural network: Numerical simulations and breadboard experiments. AEU-Int J Electron Commun 111:152894

    Article  Google Scholar 

  15. Chen C, Chen J, Bao H, Chen M, Bao B (2019) Coexisting multi-stable patterns in memristor synapse-coupled Hopfield neural network with two neurons. Nonlinear Dyn 95(4):3385–3399

    Article  MATH  Google Scholar 

  16. Dan Z, Huang W, Huang YJ (2010) Chaos and rigorous verification of horseshoes in a class of Hopfield neural networks. Neural Comput Appl 19(1):159–166

    Article  MathSciNet  Google Scholar 

  17. Duan S, Dong Z, Hu X, Wang L, Li H (2016) Applications: Small-world Hopfield neural networks with weight salience priority and memristor synapses for digit recognition. Neural Comput Appl 27(4):837–844

    Article  Google Scholar 

  18. Hopfield JJ (1995) Pattern recognition computation using action potential timing for stimulus representation. Nature 376(6535):33–36

    Article  Google Scholar 

  19. Hopfield JJ (1984) Neurons with graded response have collective computational properties like those of two-state neurons. Proc Natl Acad Sci 81(10):3088–3092

    Article  MATH  Google Scholar 

  20. Lakshmi C, Thenmozhi K, Rayappan JBB, Amirtharajan R (2019) Applications: Hopfield attractor-trusted neural network: an attack-resistant image encryption. Neural Comput Appl 13:1–13

    Google Scholar 

  21. Mathias AC, Rech PC (2012) Hopfield neural network: the hyperbolic tangent and the piecewise-linear activation functions. Neural Netw 34:42–45

    Article  Google Scholar 

  22. Njitacke Z, Kengne J, Fostin H (2019) A plethora of behaviors in a memristor based Hopfield neural networks (HNNs). Int J Dyn Control 7(1):36–52

    Article  MathSciNet  Google Scholar 

  23. Njitacke Z, Kengne J, Fozin TF, Leutcha B, Fotsin HB (2019) Dynamical analysis of a novel 4-neurons based Hopfield neural network: emergences of antimonotonicity and coexistence of multiple stable states. Int J Dyn Control 7(3):823–841

    Article  MathSciNet  Google Scholar 

  24. Njitacke ZT, Kengne J (2018) Complex dynamics of a 4D Hopfield neural networks (HNNs) with a nonlinear synaptic weight: Coexistence of multiple attractors and remerging Feigenbaum trees. AEU-Int J Electron Commun 93:242–52

    Article  Google Scholar 

  25. Njitacke ZT, Kengne J (2019) Nonlinear dynamics of three-neurons-based Hopfield neural networks (HNNs): Remerging Feigenbaum trees, coexisting bifurcations and multiple attractors. J Circuits Syst Comput 28(07):1950121

    Article  Google Scholar 

  26. Njitacke ZT, Isaac SD, Kengne J, Negou AN, Leutcho GD (2020) Extremely rich dynamics from hyperchaotic Hopfield neural network: hysteretic dynamics, parallel bifurcation branches, coexistence of multiple stable states and its analog circuit implementation. Eur Phys J Special Topics 229:1133–1154

    Article  Google Scholar 

  27. Njitacke ZT, Kengne J, Fotsin HB (2020) Coexistence of multiple stable states and bursting oscillations in a 4d Hopfield neural network. Circuits Syst Signal Process 39(7):3424–3444

    Article  MATH  Google Scholar 

  28. Xu Q, Song Z, Bao H, Chen M, Bao B (2018) Two-neuron-based non-autonomous memristive Hopfield neural network: numerical analyses and hardware experiments. AEU-Int J Electron Commun 96:66–74

    Article  Google Scholar 

  29. Xu Q, Song Z, Qian H, Chen M, Wu P, Bao B (2018) Numerical analyses and breadboard experiments of twin attractors in two-neuron-based non-autonomous Hopfield neural network. Eur Phys J Spec Top 227(7–9):777–786

    Article  Google Scholar 

  30. Yang J, Wang L, Wang Y, Guo T (2017) A novel memristive Hopfield neural network with application in associative memory. Neurocomputing 227:142–14

    Article  Google Scholar 

  31. Zheng YG, Bao LJ (2014) Slow–fast dynamics of tri-neuron Hopfield neural network with two timescales. Commun Nonlinear Sci Numer Simul 19(5):1591–1599

    Article  MathSciNet  MATH  Google Scholar 

  32. Bao B, Zhu Y, Li C, Bao H, Xu Q (2020) Global multistability and analog circuit implementation of an adapting synapse-based neuron model. Nonlinear Dyn 101:1–14

    Article  Google Scholar 

  33. Njitacke ZT, Isaac SD, Nestor T, Kengne J (2020) Window of multistability and its control in a simple 3D Hopfield neural network: application to biomedical image encryption. Neural Comput Appl. https://doi.org/10.1007/s00521-020-05451-z

    Article  Google Scholar 

  34. Gao T, Chen Z (2008) A new image encryption algorithm based on hyper-chaos. Phys Lett A 372(4):394–400

    Article  MATH  Google Scholar 

  35. Lakshmi C, Thenmozhi K, Rayappan JBB, Amirtharajan R (2020) Hopfield attractor-trusted neural network: an attack-resistant image encryption. Neural Comput Appl 32(15):11477–11489

    Article  Google Scholar 

  36. Wang X-Y, Li Z-M (2019) A color image encryption algorithm based on Hopfield chaotic neural network. Opt Lasers Eng 115:107–118

    Article  Google Scholar 

  37. Zhou Y, Cao W, Chen CP (2014) Image encryption using binary bitplane. Signal Process 100:197–207

    Article  Google Scholar 

  38. Doubla Isaac S, Njitacke ZT, Kengne J (2020) Effects of low and high neuron activation gradients on the dynamics of a simple 3D hopfield neural network. Int J Bifur Chaos 30(11):2050159

    Article  MathSciNet  MATH  Google Scholar 

  39. Kamdjeu Kengne L, Njitacke ZT, Pone JM, Tagne HK (2020) The effects of a constant excitation force on the dynamics of an infinite-equilibrium chaotic system without linear terms: analysis, control and circuit simulation. Int J Bifur Chaos 30(15):2050234

    Article  MathSciNet  MATH  Google Scholar 

  40. Bao B, Hou L, Zhu Y, Wu H, Chen M (2020) Bifurcation analysis and circuit implementation for a tabu learning neuron model. AEU-Int J Electron Commun 121:153235

    Article  Google Scholar 

  41. Wolf A, Swift JB, Swinney HL, Vastano JA (1985) Determining Lyapunov exponents from a time series. Phys D: Nonlinear Phenom 16(3):285–317

    Article  MathSciNet  MATH  Google Scholar 

  42. Strogatz SH (1994) Nonlinear dynamics and chaos. Addison-Wesley, New York

    Google Scholar 

  43. Alligood KT, Sauer TD, Yorke JA (1996) Chaos. Springer, New York

    Book  MATH  Google Scholar 

  44. Kengne J, Njitacke Z, Fotsin H (2016) Dynamical analysis of a simple autonomous jerk system with multiple attractors. Nonlinear Dyn 83(1):751–765

    Article  MathSciNet  Google Scholar 

  45. Babloyantz A, Lourenço C (1996) Brain chaos and computation. Int J Neural Syst 7(04):461–471

    Article  Google Scholar 

  46. Fortuna L, Frasca M, Rizzo A (2003) Measurement: Chaotic pulse position modulation to improve the efficiency of sonar sensors. IEEE Trans Instrum Meas 52(6):1809–1814

    Article  Google Scholar 

  47. Filali RL, Benrejeb M, Borne P, Simulation N (2014) On observer-based secure communication design using discrete-time hyperchaotic systems. Commun Nonlinear Sci Numer Simul 19(5):1424–1432

    Article  MathSciNet  MATH  Google Scholar 

  48. Duan S, Liao X (2007) An electronic implementation for Liao’s chaotic delayed neuron model with non-monotonous activation function. Phys Lett A 369(1–2):37–43

    Article  Google Scholar 

  49. Rani M, Kumar V (2004) Superior mandelbrot set. J Korea Soc Math Educ Ser D Res Math Educ 8(4):279–291

    Google Scholar 

  50. Ashton K (2009) That ‘internet of things’ thing. RFID J 22(7):97–114

    Google Scholar 

  51. Islam SR, Kwak D, Kabir MH, Hossain M, Kwak K-S (2015) The internet of things for health care: a comprehensive survey. IEEE Access 3:678–708

    Article  Google Scholar 

  52. Tsafack N, Kengne J, Abd-El-Atty B, Iliyasu AM, Hirota K, Abd EL-Latif AA (2020) Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption. Inf Sci 515:191–217

    Article  MATH  Google Scholar 

  53. Yang X, He X, Zhao J, Zhang Y, Zhang S, Xie P (2020) COVID-CT-dataset: a CT scan dataset about COVID-19. arXiv prints, arXiv: 2003.13865

  54. Hua Z, Zhou Y, Huang H (2019) Cosine-transform-based chaotic system for image encryption. Inf Sci 480:403–419

    Article  Google Scholar 

  55. Kanso A, Ghebleh M (2017) An algorithm for encryption of secret images into meaningful images. Opt Lasers Eng 90:196–208

    Article  Google Scholar 

  56. Nestor T, De Dieu NJ, Jacques K, Yves EJ, Iliyasu AM, El-Latif A, Ahmed A (2020) A multidimensional hyperjerk oscillator: dynamics analysis, analogue and embedded systems implementation, and its application as a cryptosystem. Sensors 20(1):83

    Article  Google Scholar 

  57. Sneha P, Sankar S, Kumar AS (2020) A chaotic colour image encryption scheme combining Walsh-Hadamard transform and Arnold-Tent maps. J Ambient Intell Humaniz Comput 11(3):1289–1308

    Article  Google Scholar 

  58. Tsafack N, Sankar S, Abd-El-Atty B, Kengne J, Jithin K, Belazi A, Mehmood I, Bashir AK, Song O-Y, Abd El-Latif AA (2020) A new chaotic map with dynamic analysis and encryption application in Internet of Health Things. IEEE Access 8:137731–137744

    Article  Google Scholar 

  59. Wang X, Feng L, Zhao H (2019) Fast image encryption algorithm based on parallel computing system. Inf Sci 486:340–358

    Article  MATH  Google Scholar 

  60. Alawida M, Samsudin A, Teh JS, Alkhawaldeh RS (2019) A new hybrid digital chaotic system with applications in image encryption. Signal Process 160:45–58

    Article  Google Scholar 

  61. Gong L, Qiu K, Deng C, Zhou N (2019) An image compression and encryption algorithm based on chaotic system and compressive sensing. Opt Laser Technol 115:257–267

    Article  Google Scholar 

  62. Luo Y, Yu J, Lai W, Liu L (2019) A novel chaotic image encryption algorithm based on improved baker map and logistic map. Multimedia Tools Appl 78(15):22023–22043

    Article  Google Scholar 

  63. Diaconu A-V (2016) Circular inter–intra pixels bit-level permutation and chaos-based image encryption. Inf Sci 355:314–327

    Article  Google Scholar 

  64. Jithin K, Sankar S (2020) Colour image encryption algorithm combining, Arnold map, DNA sequence operation, and a Mandelbrot set. J Inf Security Appl 50:102428

    Google Scholar 

  65. Liu L, Zhang Q, Wei X (2012) A RGB image encryption algorithm based on DNA encoding and chaos map. Comput Electr Eng 38(5):1240–1248

    Article  Google Scholar 

  66. Volos CK, Kyprianidis IM, Stouboulos IN (2013) Image encryption process based on chaotic synchronization phenomena. Signal Processing 93(5):1328–1340

    Article  Google Scholar 

  67. Modeste Nguimdo R, Tchitnga R, Woafo P (2013) Dynamics of coupled simplest chaotic two-component electronic circuits and its potential application to random bit generation. Chaos 23(4):043122

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are also grateful to the anonymous reviewers and the Associate Editor for their valuable comments, which helped improve the content of the present paper.

Funding

No funding has been used.

Author information

Authors and Affiliations

  1. Unité de Recherche D’Automatique Et Informatique Appliquée (URAIA), Department of Electrical Engineering, IUT-FV Bandjoun, University of Dschang, Dschang, Cameroon

    Isaac Sami Doubla, Zeric Tabekoueng Njitacke, Nestor Tsafack & Jacques Kengne

  2. Department of Electrical and Electronic Engineering, College of Technology (COT), University of Buea, P.O. Box 63, Buea, Cameroon

    Zeric Tabekoueng Njitacke & Sone Ekonde

  3. Unité de Recherche de Matière Condensée, d’Electronique Et de Traitement du Signal (URAMACETS), Department of Physics, University of Dschang, P.O. Box 67, Dschang, Cameroon

    Isaac Sami Doubla & Nestor Tsafack

  4. Department of Electrical Engineering and Industrial Computing, University Institute of Technology, P.O. Box 8698, Douala, Cameroon

    J. D. D. Nkapkop

Authors
  1. Isaac Sami Doubla
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zeric Tabekoueng Njitacke
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Sone Ekonde
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Nestor Tsafack
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. J. D. D. Nkapkop
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Jacques Kengne
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zeric Tabekoueng Njitacke.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Data availability

The data used in this research work are available from the authors by reasonably request.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Doubla, I.S., Njitacke, Z.T., Ekonde, S. et al. Multistability and circuit implementation of tabu learning two-neuron model: application to secure biomedical images in IoMT. Neural Comput & Applic 33, 14945–14973 (2021). https://doi.org/10.1007/s00521-021-06130-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-021-06130-3

Keywords