Skip to main content

Advertisement

Springer Nature Link
Log in

Multi-view subspace clustering with adaptive locally consistent graph regularization

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

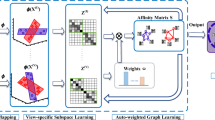
Graph regularization has shown its effectiveness in multi-view subspace clustering methods. Many multi-view subspace clustering methods based on graph regularization build the adjacency matrix directly based on a simple similarity measure between data points for each view. However, these simply constructed graphs are sensitive to light corruptions and even generate misleading manifold. Considering this shortcoming, this paper presents a multi-view subspace clustering algorithm (CGMSC) with a well-defined locally consistent graph regularization. We formulate CGMSC by a two-stage procedure. In the first stage, an adaptive self-weighted multi-view local linear embedding (ASWMVLLE) method is proposed to build the locally consistent geometric relationship between instances. In the second stage, ASWMVLLE is introduced into CGMSC by defining a local graph regularization term about the consensus latent subspace representation, which can not only effectively keep the manifold structure of data, but also ensure the consistency across different views. Experiments on eight real-world datasets demonstrate that our method has good robustness and clustering performance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Notes

  1. http://mlg.ucd.ie/datasets/3sources.html.

  2. http://mlg.ucd.ie/datasets/bbc.html.

  3. http://lig-membres.imag.fr/grimal/data.html.

  4. http://cam-orl.co.uk/facedatabase.html.

  5. http://archive.ics.uci.edu/ml/datasets/multiple+features.

  6. https://www1.cs.columbia.edu/CAVE/software/softlib/coil-100.php.

  7. http://www.vision.caltech.edu/Image_Datasets/Caltech101/.

References

  1. Abavisani M, Patel VM (2018) Multimodal sparse and low-rank subspace clustering. Inf Fusion 39:168–177

    Article  Google Scholar 

  2. Aditya K, Ayan S, Ondrej K, Gonzalo-martin C (2019) Fuzzy k-means using non-linear s-distance. IEEE Access 7:55121–55131

    Article  Google Scholar 

  3. Ayan S, Aditya K, Ondrej K, Consuelo GM (2020) Fuzzy c-means clustering using Jeffreys-divergence based similarity measure. Appl Soft Comput J 88:106016

    Article  Google Scholar 

  4. Brbić M, Kopriva I (2018) Multi-view low-rank sparse subspace clustering. Pattern Recognit 73:247–258

    Article  Google Scholar 

  5. Cai D, He X, Han J (2011) Locally consistent concept factorization for document clustering. IEEE Trans Knowl Data Eng 23(6):902–913

    Article  Google Scholar 

  6. Cao X, Zhang C, Fu H, Si Liu, Hua Zhang (2015) Diversity-induced multi-view subspace clustering. In: 2015 IEEE conference on computer vision and pattern recognition (CVPR), IEEE, vol 07-12-June, pp 586–594

  7. Chen Y, Xiao X, Zhou Y (2020) Multi-view subspace clustering via simultaneously learning the representation tensor and affinity matrix. Pattern Recognit 106:107441

    Article  Google Scholar 

  8. Elhamifar E, Vidal R (2013) Sparse subspace clustering: algorithm, theory, and applications. IEEE Trans Pattern Anal Mach Intell 35(11):2765–2781

    Article  Google Scholar 

  9. Gao H, Nie F, Li X, Huang H (2015) Multi-view Subspace Clustering. In: 2015 IEEE international conference on computer vision (ICCV), IEEE, vol 2015, pp 4238–4246

  10. He X, Niyogi P (2004) Locality preserving projections. In: Advances in neural information processing systems, NIPS 2004. MIT Press, pp 153–160

  11. He X, Kan MY, Xie P, Chen X (2014) Comment-based multi-view clustering of web 2.0 items. In: Proceedings of the 23rd international conference on World wide web—WWW ’14. ACM Press, pp 771–782

  12. Kivinen J, Warmuth MK (1997) Exponentiated gradient versus gradient descent for linear predictors. Inf Comput 132(1):1–63

    Article  MathSciNet  Google Scholar 

  13. Krishna KS, Ayan S (2020) Clustering analysis using an adaptive fused distance. Eng Appl Artif Intell 96:103928

    Article  Google Scholar 

  14. Krishna KS, Ayan S (2021) Spectral embedded generalized mean based \(k\)-nearest neighbors clustering with s-distance. Expert Syst Appl 169:114326

    Article  Google Scholar 

  15. Kumar A, Rai P, Daumé H (2011) Co-regularized multi-view spectral clustering. In: Advances in neural information processing systems. Curran Associates, Inc., vol 24, pp 1413–1421

  16. Lee DD, Seung HS (1999) Learning the parts of objects by non-negative matrix factorization. Nature 401(6755):788–791

    Article  Google Scholar 

  17. Liu G, Lin Z, Yan S, Sun J, Yu Y, Ma Y (2013) Robust recovery of subspace structures by low-rank representation. IEEE Trans Pattern Anal Mach Intell 35(1):171–184

    Article  Google Scholar 

  18. Liu J, Wang C, Gao J, Han J (2013) Multi-view clustering via joint nonnegative matrix factorization. In: Proceedings of the 2013 SIAM international conference on data mining, society for industrial and applied mathematics, pp 252–260

  19. Luo S, Zhang C, Zhang W, Cao X (2018) Consistent and specific multi-view subspace clustering. In: 32nd AAAI conference on artificial intelligence, AAAI 2018. AAAI Press, pp 3730–3737

  20. Ng AY, Jordan MI, Weiss Y (2002) On spectral clustering: analysis and an algorithm. In: Advances in neural information processing systems. MIT Press, vol 14, pp 849–856

  21. Nie F, Li J, Li X (2016) Parameter-free auto-weighted multiple graph learning: s framework for multiview clustering and semi-supervised classification. In: 27th International joint conference on artificial intelligence, IJCAI 2016. AAAI Press, pp 1881–1887

  22. Pei X, Chen C, Gong W (2018) Concept factorization with adaptive neighbors for document clustering. IEEE Trans Neural Netw Learn Syst 29(2):343–352

    Article  MathSciNet  Google Scholar 

  23. Peng X, Tang H, Zhang L, Yi Z, Xiao S (2016) A unified framework for representation-based subspace clustering of out-of-sample and large-scale data. IEEE Trans Neural Netw Learn Syst 27(12):2499–2512

    Article  MathSciNet  Google Scholar 

  24. Rao S, Tron R, Vidal R, Ma Y (2010) Motion segmentation in the presence of outlying, incomplete, or corrupted trajectories. IEEE Trans Pattern Anal Mach Intell 32(10):1832–1845

    Article  Google Scholar 

  25. Roweis ST, Saul LK (2000) Nonlinear dimensionality reduction by locally linear embedding. Science 290(5500):2323–2326

    Article  Google Scholar 

  26. Vidal R, Favaro P (2014) Low rank subspace clustering (LRSC). Pattern Recognit Lett 43(1):47–61

    Article  Google Scholar 

  27. Wang J, Tian F, Yu H, Liu CH, Zhan K, Wang X (2018) Diverse non-negative matrix factorization for multiview data representation. IEEE Trans Cybern 48(9):2620–2632

    Article  Google Scholar 

  28. Wang YX, Xu H, Leng C (2019) Provable subspace clustering: when LRR meets SSC. IEEE Trans Inf Theory 65(9):5406–5432

    Article  Google Scholar 

  29. Xie Y, Zhang W, Qu Y, Dai L, Tao D (2020) Hyper-Laplacian regularized multilinear multiview self-representations for clustering and semisupervised learning. IEEE Trans Cybern 50(2):572–586

    Article  Google Scholar 

  30. Yan Y, Hao W (2018) Multi-view clustering: a survey. Big Data Min Anal 1(2):83–107

    Article  Google Scholar 

  31. Zhang H, Patel VM, Chellappa R (2015) Robust multimodal recognition via multitask multivariate low-rank representations. In: 2015 11th IEEE international conference and workshops on automatic face and gesture recognition, FG 2015, IEEE, pp 1–8

  32. Zhang X, Phung D, Venkatesh S, Pham DS, Liu W (2015) Multi-view subspace clustering for face images. In: 2015 International conference on digital image computing: techniques and applications, DICTA 2015, IEEE, pp 1–7

  33. Zhang X, Gao H, Li G, Zhao J, Huo J, Yin J, Liu Y, Zheng L (2018) Multi-view clustering based on graph-regularized nonnegative matrix factorization for object recognition. Inf Sci 432:463–478

    Article  MathSciNet  Google Scholar 

  34. Zhao Y, Chen L, Chen C (2021) Laplacian regularized nonnegative representation for clustering and dimensionality reduction. IEEE Trans Circuits Syst Video Technol 31(1):1–14

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (NSFC) [Grant Numbers 61502175, 61273295]; and the Natural Science Foundation of Guangdong Province [Grant Number 2020A1515010699].

Author information

Authors and Affiliations

  1. School of Mathematics, South China University of Technology, Guangzhou, China

    Xiaolan Liu

  2. Kou Kou Xiang Chuan (Hangzhou) Network Technology Co., Ltd., Hangzhou, China

    Gan Pan

  3. School of Software Engineering, South China University of Technology, Guangzhou, China

    Mengying Xie

Authors
  1. Xiaolan Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Gan Pan
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Mengying Xie
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mengying Xie.

Ethics declarations

Conflict of interest

We confirm that there is no conflict of interest associated with this paper. The manuscript has been read and approved by all named authors, and the order of authors listed in the manuscript has been approved by all of us. We confirm that there are no impediments to publication with respect to intellectual property.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, X., Pan, G. & Xie, M. Multi-view subspace clustering with adaptive locally consistent graph regularization. Neural Comput & Applic 33, 15397–15412 (2021). https://doi.org/10.1007/s00521-021-06166-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-021-06166-5

Keywords