Exponential synchronization of fractional-order multilayer coupled neural networks with reaction-diffusion terms via intermittent control

Abstract

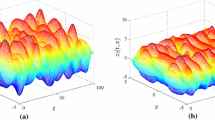
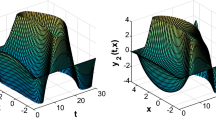
In this paper, the issue of exponential synchronization of fractional-order multilayer coupled neural networks with reaction-diffusion terms is investigated by using periodically intermittent control. It deserves to mention that spatial diffusions, multilayer interactions and fractional dynamics are introduced to coupled neural networks at the same time. A novel fractional-order differential inequality is established on the basis of Caputo partial fractional operator. Moreover, to realize exponential synchronization of the underlying neural networks, some sufficient conditions are presented with the help of Lyapunov method and graph theory. Theoretical results show that the exponential convergence rate is dependent on the control gain and the order of fractional derivative. Finally, an illustrative numerical example is provided to further verify the feasibility and effectiveness of our results.

Appendices

Appendix A

Proof

Since matrix ${\hat{M}}$ is a symmetric and positive definite matrix, there exists an orthogonal matrix $P\in {\mathbb {R}}^{n\times n}$ and a diagonal matrix $\Lambda =\mathrm {diag}\{\lambda _{1},\lambda _{2},\ldots , \lambda _{n}\}\in {\mathbb {R}}^{n\times n}$ such that $P\Lambda P^{\mathrm {T}}={\hat{M}}$, in which $\lambda _{i}>0$. Then, we can see that

$$\begin{aligned} \Psi ^{\mathrm {T}}(x,t){\hat{M}}\Psi (x,t)&= {} \Psi ^{\mathrm {T}}(x,t)P\Lambda P^{\mathrm {\mathrm {T}}}\Psi (x,t)\nonumber \\&= {} \left( P^{\mathrm {T}}\Psi (x,t)\right) ^{\mathrm {T}}\Lambda \left( P^{\mathrm {T}}\Psi (x,t)\right) . \end{aligned}$$

(19)

Let $\Phi (x,t)=P^{\mathrm {T}}\Psi (x,t)$, where $\Phi (x,t)=\left( \Phi _{1}(x,t),\Phi _{2}(x,t),\ldots ,\Phi _{n}(x,t)\right) ^{\mathrm {T}}$. According to (19), one has

$$\begin{aligned} \Psi ^{\mathrm {\mathrm {T}}}(x,t){\hat{M}}\Psi (x,t) =\Phi ^{\mathrm {T}}(x,t)\Lambda \Phi (x,t). \end{aligned}$$

Noticing that $\Lambda$ is diagonal, we derive$\Phi ^{\mathrm {T}}(x,t)\Lambda \Phi (x,t)=\sum _{i=1}^{n}\lambda _{i}\Phi _{i}^{2}(x,t).$ That is to say for $\forall \alpha \in (0,1],~t\ge t_{0}$

$$\begin{aligned} {}_{t_{0}}^{C}{D_{t}^{\alpha }}\Phi ^{\mathrm {T}}(x,t)\Lambda \Phi (x,t)&= {} {}_{t_{0}}^{C}{D_{t}^{\alpha }}\sum _{i=1}^{n}\lambda _{i} \Phi _{i}^{2}(x,t)\nonumber \\&= {} \sum _{i=1}^{n}\lambda _{i}~ {}_{t_{0}}^{C}{D_{t}^{\alpha }}\Phi _{i}^{2}(x,t). \end{aligned}$$

(20)

Applying Lemma 3, due to $\lambda _{i}>0$, in line with (20), it is obtained that

$$\begin{gathered} _{{t_{0} }}^{C} D_{t}^{\alpha } \Phi ^{{\text{T}}} (x,t)\Lambda \Phi (x,t) \hfill \\ \le 2\sum\limits_{{i = 1}}^{n} {\lambda _{i} } \Phi _{i}^{{\text{T}}} (x,t)_{{t_{0} }}^{C} D_{t}^{\alpha } \Phi _{i} (x,t). \hfill \\ \end{gathered}$$

(21)

Since $\lambda _{i}$ is the diagonal element of matrix $\Lambda$, it is clear that

$$\begin{aligned} \sum _{i=1}^{n}\lambda _{i}\Phi _{i}^{\mathrm {T}} (x,t){}_{t_{0}}^{C}{D_{t}^{\alpha }}\Phi _{i}(x,t) =\Phi ^{\mathrm {T}}(x,t)\Lambda {}_{t_{0}}^{C}{D_{t}^{\alpha }}\Phi (x,t). \end{aligned}$$

Consequently, combined with (21), for $\forall \alpha \in (0,1],~t\ge t_{0}$, we state that

$$\begin{aligned} {}_{t_{0}}^{C}{D_{t}^{\alpha }}\Phi ^{\mathrm {T}}(x,t) \Lambda \Phi (x,t)\le 2\Phi ^{\mathrm {T}}(x,t)\Lambda {}_{t_{0}}^{C}{D_{t}^{\alpha }}\Phi (x,t). \end{aligned}$$

Considering $\Phi (x,t)=P^{\mathrm {T}}\Psi (x,t)$, for $\forall \alpha \in (0,1],~t\ge t_{0}$, we obtain

$$\begin{gathered} _{{t_{0} }}^{C} D_{t}^{\alpha } \left( {P^{{\text{T}}} \Psi (x,t)} \right)^{{\text{T}}} \Lambda \left( {P^{{\text{T}}} \Psi (x,t)} \right) \hfill \\ \le 2\left( {P^{{\text{T}}} \Psi (x,t)} \right)^{{\text{T}}} \Lambda _{{t_{0} }}^{C} D_{t}^{\alpha } \left( {P^{{\text{T}}} \Psi (x,t)} \right). \hfill \\ \end{gathered}$$

(22)

Rearranging and using $P\Lambda P^{\mathrm {T}}={\hat{M}}$ into (22), for $\forall \alpha \in (0,1],~t\ge t_{0}$, it is concluded that

$$\begin{aligned} {}_{t_{0}}^{C}{D_{t}^{\alpha }}\Psi ^{\mathrm {T}}(x,t) {\hat{M}}\Psi (x,t)\le 2\Psi ^{\mathrm {T}}(x,t){\hat{M}}{}_{t_{0}}^{C}{D_{t}^{\alpha }}\Psi (x,t). \end{aligned}$$

This completes the proof. $\square$

Appendix B

Proof

When $t\in T_m^c$, in view of (5), there is a nonnegative function A(t) such that

$$\begin{aligned} {}_{T_{m}}^{C}{D_{t}^{\alpha }}V(t)+A(t)=-\zeta _{1}V(t). \end{aligned}$$

(23)

Taking Laplace transform of (23), we have

$$\begin{aligned} s^{\alpha }{\mathbb {V}}(s)+s^{\alpha -1}{\mathbb {V}}(T_{m})+{\mathbb {A}}(s) =-\zeta _{1}{\mathbb {V}}(s), \end{aligned}$$

(24)

where ${\mathbb {V}}(s)$ and ${\mathbb {A}}(s)$ denote the Laplace transform of V(t) and A(t), respectively. Then, taking inverse Laplace transform of (24), we get

$$\begin{aligned} V(t)&= {} V(T_{m})E_{\alpha }\left( -\zeta _{1}(t-T_{m})^{\alpha }\right) \\&-A(t)*\left\{ \left( t-T_{m}\right) ^{\alpha }E_{\alpha ,\alpha } \left( -\zeta _{1}\left( t-T_{m}\right) ^{\alpha }\right) \right\} , \end{aligned}$$

where $*$ represents the convolution operator. Since $(t-T_{m})^{\alpha }$ and $E_{\alpha ,\alpha }(-\zeta _{1}\left( t-T_{m}\right) ^{\alpha })$ are nonnegative functions, it yields that

$$\begin{aligned} V(t)\le V(T_{m})E_{\alpha }(-\zeta _{1}\left( t-T_{m}\right) ^{\alpha }). \end{aligned}$$

When $t\in T_m^r$, based on (5), there exists a nonnegative function B(t) such that

$$\begin{aligned} {}_{T_{m}+\theta }^{C}{D_{t}^{\alpha }}V(t)+B(t)=\zeta _{2}V(t). \end{aligned}$$

(25)

Similarly to the case of $t\in T_m^c$, for (25), one obtain

$$\begin{aligned} V(t)&= {} V(T_{m}+\theta )E_{\alpha }\left( \zeta _{2}(t-(T_{m}+\theta ))^{\alpha }\right) -B(t)\\&\times \left\{ \left( t-(T_{m}+\theta )\right) ^{\alpha } E_{\alpha ,\alpha }\left( \zeta _{2}\left( t-(T_{m}+\theta )\right) ^{\alpha }\right) \right\} . \end{aligned}$$

Hence, owing to the nonnegativity of $(t-(T_{m}+\theta ))^{\alpha }$ and $E_{\alpha ,\alpha }(\zeta _{2}\left( t-(T_{m}+\theta )\right) ^{\alpha })$, it follows that

$$\begin{aligned} V(t)\le V(T_{m}+\theta )E_{\alpha }(\zeta _{2}(t-(T_{m}+\theta ))^{\alpha }). \end{aligned}$$

This proof is now completed. $\square$