Evolutionary algorithm applied to time-series landing flight path and control optimization of supersonic transport

Abstract

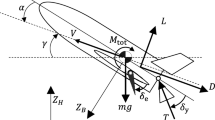
An evolutionary algorithm (EA) was applied in this study to optimize the landing flight path of a delta-winged supersonic transport (SST). However, it is difficult for a delta wing with a large sweepback angle to reduce the aerodynamic drag during supersonic cruising to gain sufficient lift force at low speeds, particularly during takeoff and landing. Besides, high-fidelity computational fluid dynamics is required to evaluate the flight path with a complex flowfield. This study performed an efficient flight simulation based on the Kriging model-assisted aerodynamic estimation to carry out global optimization. Then, the designs of the flight and control sequence were realized for time-series optimization of effective SST landing. To develop the EA, two design scenarios were considered; one involved only the elevator, which is an aerodynamic control surface that controls the aircraft, and the other involved introducing thrust control in addition to elevator control. In the scenario involving only elevator control, feasible solutions could not be obtained owing to the poor low-speed aerodynamic performance of the SST. This paper presents several feasible solutions enabling reasonable SST landing performance in the scenario involving the elevator and thrust controls along with descriptions regarding the optimum flight and control sequences. In addition, we analyzed the solutions by analyzing the variance to obtain qualitative information. Consequently, we determined that elevator control was considerably effective in cases with the microburst effect than in cases without the microburst effect.

Appendices

Appendix 1: Prior study for establishing EA conditions

We investigated appropriate EA operations, such as generation numbers, crossover methods, and mutation methods for the present study. First, we determined the crossover method via Problem1. Blended crossover (BLX) [27] and simulated binary crossover (SBX) [16] were compared. As shown in Fig. 14, objective function $w(t_{\mathrm{f}})$ in SBX converged earlier than those in BLX. Thus, we chose SBX for this study. Then, two mutation methods, polynomial mutation (PM) [16] and uniform mutation (UM), were also compared with SBX. As shown in Fig. 14, the result obtained via the use of PM and UM were almost the same. Thus, we chose PM which was originally applied in NSGA-II[16] for this study.

Finally, we determined the maximum generation number by investigating convergence histories. As shown in Fig. 14, each objective function of Problem1 converged well after 15 000 generations. Thus, the generation number was set as 30 000. In Problem2, which is a three-objective problem, each objective converged; in particular, J converged well after 25 000 generations, as shown in Fig 15. Considering the simulation cost and the need for practical solutions, we fixed the total number of generations at 30 000 in each problem.

Fig. 14

Comparison of convergence history of EA

Fig. 15

Convergence history of EA

Appendix 2: Trajectory Range Decided Based on ILS Guidance

In this study, the flight was assumed to be initiated under the following preliminary conditions: $x(0)=0$ [m]; $z(0)=250$ [m]; $M(0)=0.35$; $\alpha (0)=5.1$ [$^\circ$]; $T(0)=17719.0$ [N]; and $\delta _{\mathrm{e}}(0)=-26.0$. x(0), $z(0)=250$, and M(0) were determined referring to the Concord flight [23] and according to the glide slope[25] directed by the ILS, as shown in Fig. 16. In this study, the upper limit of the glide slope was considered, and the aircraft started at six $^circ$ from the horizontal line. Thus, the aircraft had to fly 4770.0 m.

Fig. 16

Definition of the flight conditions using ILS