Skip to main content

Advertisement

Springer Nature Link
Log in

New results on finite-time stability of fractional-order neural networks with time-varying delay

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

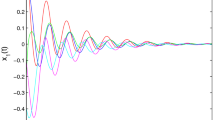
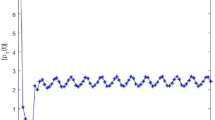
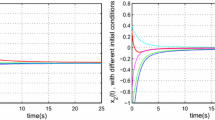
In this paper, we propose an analytical approach based on the Laplace transform and Mittag–Leffler functions combining with linear matrix inequality techniques to study finite-time stability of fractional-order neural networks (FONNs) with time-varying delay. The concept of finite-time stability is extended to the fractional-order neural networks and the delay function is assumed to be non-differentiable, but continuous and bounded. We first prove some important lemmas on the existence of solutions and on estimation of the Caputo derivative of specific quadratic functions. Then, new delay-dependent sufficient conditions for finite-time stability of FONNs with time-varying delay are derived in terms of a tractable linear matrix inequality and Mittag–Leffler functions. Finally, a numerical example with simulations is provided to demonstrate the effectiveness and validity of the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Forti F, Tesi A (1995) New conditions for global stability of neural networks with application to linear and quadratic programming problems, IEEE Trans Circuits Syst I Funda Theory Appl. 42(7), 354–366

    Article  MathSciNet  Google Scholar 

  2. Arik S (2002) An analysis of global asymptotic stability of delayed cellular neural networks. IEEE Trans. on Neural Netw. 3(5), 1239–1242

    Article  Google Scholar 

  3. Gupta D, Cohn LF (2012) Intelligent transportation systems and NO2 emissions: Predictive modeling approach using artificial neural networks. J. Infrastruct. Syst. 18(2), 113–118

    Article  Google Scholar 

  4. Phat VN, Fernando T, Trinh H (2014) Observer-based control for time-varying delay neural networks with nonlinear observation. Neural Computing and Applications 24:1639–1645

    Article  Google Scholar 

  5. Abdelsalam SI, Velasco-Hernandez JX, Zaher A.Z. (2012) Electro-magnetically modulated self-propulsion of swimming sperms via cervical canal. Biomechanics and Modeling in Mechanobiology 20:861–878

    Article  Google Scholar 

  6. Abdesalam SI, Bhatti MM (2020) Anomalous reactivity of thermo-bioconvective nanofluid towards oxytactic microorganisms. Applied Mathematics and Mechanics 41:711–724

    Article  MathSciNet  Google Scholar 

  7. Kilbas AA, Srivastava H, Trujillo J (2006) Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam

    MATH  Google Scholar 

  8. Bhatti MM, Alamri SZ, Ellahi R, Abdelsalam S.I. (2021) Intra-uterine particle-fluid motion through a compliant asymmetric tapered channel with heat transfer. Journal of Thermal Analysis and Calorimetry 144:2259–2267

    Article  Google Scholar 

  9. Elmaboud Y.A., Abdelsalam S.I., (2019), DC/AC magnetohydro dynamic-micropump of a generalized Burger’s fluid in an annulus, Physica Scripta, 94(11): 115209

    Article  Google Scholar 

  10. Lundstrom B, Higgs M, Spain W, Fairhall A (2008) Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 11:1335–1342

    Article  Google Scholar 

  11. Zhang S, Yu Y, Wang H (2015) Mittag-Leffler stability of fractional-order Hopfield neural networks. Nonlinear Anal. Hybrid Syst. 16:104–121

    Article  MathSciNet  Google Scholar 

  12. Chen L, Liu C, Wu R et al. (2016) Finite-time stability criteria for a class of fractional-order neural networks with delay. Neural Computing and Applications 27:549–556

    Article  Google Scholar 

  13. Liu S, Yu Y, Zhang S (2019) Robust synchronization of memristor-based fractional-order Hopfield neural networks with parameter uncertainties. Neural Computing and Applications 31:3533–3542

    Article  Google Scholar 

  14. Baleanu D, Asad JH, Petras I (2012) Fractional-order two-electric pendulum. Romanian Reports in Physics 64(4), 907–914

    Google Scholar 

  15. Baleanu D, Petras I, Asad JH, Velasco MP (2012) Fractional Pais-Uhlenbeck oscillator. International Journal of Theoretical Physics 51(4), 1253–1258

    Article  Google Scholar 

  16. Baleanu D, Asad JH, Petras I (2015) Numerical solution of the fractional Euler-Lagrange’s equations of a thin elastica model. Nonlinear Dynamics 81(1–2), 97–102

    Article  MathSciNet  Google Scholar 

  17. Dorato P (1961) Short time stability in linear time-varying systems. Proceedings of IRE International Convention Record 4:83–87

    Google Scholar 

  18. Amato F, Ambrosino R, Ariola M, Cosentino C (2014) Finite-Time Stability and Control Lecture Notes in Control and Information Sciences, Springer, New York

    Book  Google Scholar 

  19. Cai M, Xiang Z (2015) Adaptive fuzzy finite-time control for a class of switched nonlinear systems with unknown control coefficients. Neurocomputing 162:105–115

    Article  Google Scholar 

  20. Fan Y, Li Y (2020) Adaptive fuzzy finite-time optimal control for switched nonlinear systems. Appl Meth Optimal Contr. doi: https://doi.org/10.1002/oca.2623

    Article  MATH  Google Scholar 

  21. Ruan Y., Huang T. (2020), Finite-time control for nonlinear systems with time-varying delay and exogenous disturbance, Symmetry, 12(3): 447

    Article  Google Scholar 

  22. Lazarevi MP, Spasi AM (2009) Finite-time stability analysis of fractional order time-delay systems: Gronwall’s approach. Math. Comput. Model. 49:475–481

    Article  MathSciNet  Google Scholar 

  23. Phat VN, Thanh NT (2018) New criteria for finite-time stability of nonlinear fractional-order delay systems: A Gronwall inequality approach. Appl. Math. Letters 83:169–175

    Article  MathSciNet  Google Scholar 

  24. Ye H, Gao J, Ding Y (2007) A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 328:1075–1081

    Article  MathSciNet  Google Scholar 

  25. Yang X, Song Q, Liu Y, Zhao Z (2015) Finite-time stability analysis of fractional-order neural networks with delay. Neurocomputing 152:19–26

    Article  Google Scholar 

  26. Chen L, Liu C, Wu R, He Y, Chai Y (2016) Finite-time stability criteria for a class of fractional-order neural networks with delay. Neural Computing and Applications 27:549–556

    Article  Google Scholar 

  27. Wu RC, Lu YF, Chen LP (2015) Finite-time stability of fractional delayed neural networks. Neurocomputing 149:700–707

    Article  Google Scholar 

  28. Xu C, Li P (2019) On finite-time stability for fractional-order neural networks with proportional delays. Neural Processing Letters 50:1241–1256

    Article  Google Scholar 

  29. Rajivganthi C, Rihan FA, Lakshmanan S, Muthukumar P (2018) Finite-time stability analysis for fractional-order Cohen-Grossberg BAM neural networks with time delays. Neural Computing and Applications 29:1309–1320

    Article  Google Scholar 

  30. Hua C, Zhang T, Li Y, Guan X (2016) Robust output feedback control for fractional-order nonlinear systems with time-varying delays. IEEE/CAA J. Auto. Sinica 3:47–482

    MathSciNet  Google Scholar 

  31. Zhang H, Ye R, Cao J, Ahmed A et al. (2018) Lyapunov functional approach to stability analysis of Riemann-Liouville fractional neural networks with time-varying delays, Asian. J. Control 20:1–14

    Article  MathSciNet  Google Scholar 

  32. Zhang H, Ye R, Liu S et al. (2018) LMI-based approach to stability analysis for fractional-order neural networks with discrete and distributed delays. Int. J. Syst. Science 49:537–545

    Article  MathSciNet  Google Scholar 

  33. Zhangand F, Zeng Z (2020) Multistability of fractional-order neural networks with unbounded time-varying delays. Neural Netw Lean Syst IEEE Trans https://doi.org/10.1109/TNNLS.2020.2977994

    Article  Google Scholar 

  34. Thanh NT, Niamsup P, Phat VN (2020) New finite-time stability analysis of singular fractional differential equations with time-varying delay. Frac. Calcul. Anal. Appl. 23:504–517

    Article  MathSciNet  Google Scholar 

  35. Sau NH, Hong DT, Huyen NT, et al. (2021) Delay-dependent and order-dependent \(H_\infty \) control for fractional-order neural networks with time-varying delay. Equ Dyn Syst Diff. doi: https://doi.org/10.1007/s12591-020-00559-z

    Article  Google Scholar 

  36. Vainikko G (2016) Which functions are fractionally differentiable. Zeitschrift fuer Analysis und Ihre Anwendungen 35:465–48

    Article  MathSciNet  Google Scholar 

  37. Cheng J, Zhong S, Zhong Q, Zhu H, Du YH (2014) Finite-time boundedness of state estimation for neural networks with time-varying delays. Neurocomputing 129:257–264

    Article  Google Scholar 

  38. Prasertsang P, Botmart T (2021) Improvement of finite-time stability for delayed neural networks via a new Lyapunov-Krasovskii functional. AIMS Mathematics 6(1), 998–1023

    Article  MathSciNet  Google Scholar 

  39. Saravanan S., Ali M. S. (2018), Improved results on finite-time stability analysis of neural networks with time-varying delays, J. Dyn. Sys. Meas. Control., 140(10): 101003

    Article  Google Scholar 

  40. Gahinet P, Nemirovskii A, Laub AJ, Chilali M (1985) LMI Control Toolbox For use with Matlab. The MathWorks Inc, Massachusetts

    Google Scholar 

Download references

Acknowledgements

This paper was written when the authors were studying at the Vietnam Institute for Advanced Study in Mathematics (VIASM). We sincerely thank the Institute for support and hospitality. The research of N.T. Thanh and V.N. Phat is supported by National Foundation for Science and Technology Development (No. 101.01-2021.01). The research of P. Niamsup is supported by the Chiang Mai University, Thailand. The authors wish to thank the associate editor and anonymous reviewers for valuable comments and suggestions, which allowed us to improve the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Mining and Geology, Hanoi, Vietnam

    Nguyen T. Thanh

  2. RCMAM, Department of Mathematics, Chiang Mai University, Chiang Mai, 50200, Thailand

    P. Niamsup

  3. ICRTM, Institute of Mathematics, VAST, 18 Hoang Quoc Viet Road, Hanoi, 10307, Vietnam

    Vu N. Phat

Authors
  1. Nguyen T. Thanh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. P. Niamsup
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Vu N. Phat
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Vu N. Phat.

Ethics declarations

Conflict of interest

The authors declare that no potential conflict of interest to be reported to this work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Thanh, N.T., Niamsup, P. & Phat, V.N. New results on finite-time stability of fractional-order neural networks with time-varying delay. Neural Comput & Applic 33, 17489–17496 (2021). https://doi.org/10.1007/s00521-021-06339-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-021-06339-2

Keywords