Causal discovery from multi-domain data using the independence of modularities

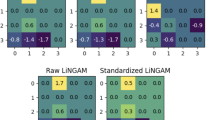
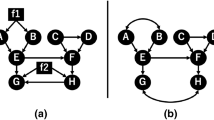
Abstract

Finding a causal relationship that can be generalized in different scenarios is a fundamental problem in science. However, in real-world scenarios, it commonly encounters a distribution shift, of which the underlying generating process changes across the domains. Such a distribution shift brings the challenge to the causal discovery from observational data, as most of the current models assume a fixed causal mechanism in heterogeneous data. As a consequence, the causal direction fails to be identified. Fortunately, in a general causal system, the distributions in the causal direction (but not the anti-causal direction) change independently across the domains, which inspires a way for causal discovery in the multi-domain data by measuring the independent change. By investigating the modularity of the causal mechanism in the multi-domain discretization data, we establish theoretical results on the identification of the causal direction under a mild technical condition. One step further, by utilizing the discretization technique, we propose a general framework for causal direction identification in the multi-domain data without assuming the specific causal mechanism and data types. We verify the effectiveness of our proposed methods in synthetic data and successfully identified the causal direction in two real-world datasets.