Skip to main content

Advertisement

Springer Nature Link
Log in

An improved spatial point cloud simplification algorithm

  • S.I.: Machine Learning based semantic representation and analytics for multimedia application
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

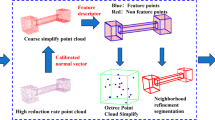
Conventional data simplification algorithms depend much on scanning technology. However, with the development of the scanning technology, the conventional algorithm is unable to process numerous redundant data, leading to increased noise of point cloud data, failure of locating split center, and low simplification efficiency. In order to remove the noise in point cloud data, improve randomness for choosing the segmentation center, and obtain robust curvature information of the point cloud data and accurate segmentation results, the following improvements are made to the conventional spatial segmentation algorithms in this paper. Firstly, on the basis of denoising by B-spline wavelet filtering, voxel grid of point cloud data is carried out to select the effective segmentation center. Secondly, through the improvement of the subspace clustering algorithm, reasonable space division can be realized. Thirdly, based on the first-order neighbourhood surface of the vertices of the mesh surface, the curvature of sample points can be estimated. Fourthly, by introducing the distance between the neighbourhood sample and the target sample, the distance between the two points is taken as the geodesic distance, the smooth correction of the estimated result can be realized and the finally simplified point cloud segmentation result can be obtained. Finally, a robust spatial data simplification method is implemented. The experimental results show that this method can further segment spatial data and obtain simplified segmentation results while ensuring segmentation efficiency. Compared with the unified sampling method, the curvature simplification method, the isometric sampling method, and the random sampling method, the proposed method can reduce the sensitivity to boundary noise data, solve the problem of fuzzy boundary division, and overcome the disadvantage of poor accuracy caused by too high dimension.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Bracco C, Davydov O, Giannelli C, Sestini A (2019) Fault and gradient fault detection and reconstruction from scattered data. Comp. Aided Geom. Des 75:101786. https://doi.org/10.1016/j.cagd.2019.101786

    Article  MathSciNet  MATH  Google Scholar 

  2. Nguyen DP, Tho MCHB, Dao TT (2021) Enhanced facial expression recognition using 3D point sets and geometric deep learning. Med Biol Eng Compu 79:61235–61244. https://doi.org/10.1007/s11517-021-02383-1

    Article  Google Scholar 

  3. Zhiqi Li, Yingkui Zhang, Yidan Feng, Xingyu Xie, Qiong Wang, Mingqiang Wei, Pheng-Ann Heng. (2020). NormalF-Net: Normal Filtering Neural Network for Feature-preserving Mesh Denoising. 127:102861, https://doi.org/10.1016/j.cad.2020.102861

  4. Liu Z, Xiao X, Zhong S et al (2020) A feature-preserving framework for point cloud denoising. Comput Aided Des 127:102857. https://doi.org/10.1016/j.cad.2020.102857

    Article  MathSciNet  Google Scholar 

  5. Dening Lu, Xuequan Lu, Yangxing Sun, Jun Wang. (2020).Deep feature-preserving normal estimation for point cloudfiltering.125:102860.Computer-Aided Design,https://doi.org/10.1016/j.cad.

  6. Martin Skrodzki, Eric Zimmermann, Konrad Polthier.(2020) " Variational shape approximation of point set surfaces" Computer-Aided Design. Computer Aided Geometric Design, 80:101875.https://doi.org/10.1016/j.cagd.2020.101875

  7. Yue S, Li N, Wang W, Wang H, Bao M, Jiang Bo (2020) Linear Interpolation Based Adaptive Feature-Preserving Filtering Method on Mesh Models 32(9):1377–1388. https://doi.org/10.3724/sp.j.1089.2020.18104

    Article  Google Scholar 

  8. Nakagawa M, Image PCCUPLR (2018) Laser & Optoelectronics Progress. Math Probl Eng 9(9):091002. https://doi.org/10.1155/2020/5713137

    Article  Google Scholar 

  9. Yang Y , Li M , Ma X .(2020). Point Cloud Simplification Method Based on Modified Fuzzy C-Means Clustering Algorithm with Feature Information Reserved. Mathematical Problems in Engineering, 2020(4):1–13. https://doi.org/10.1155/2020/5713137

  10. Hans H.C. Bejar, Silvio Jamil Ferzoli Guimaraes, Paulo A.V. Miranda. Efficient hierarchical graph partitioning for image segmentation by optimum oriented cuts. Pattern Recognit. Lett. 131:185–192. https://doi.org/10.1016/j.patrec.2020.01.008

  11. Haoyan Xu, Duan Z, Wang Y, Feng J, Chen R, Zhang Q, Zhongbin Xu (2021) Graph partitioning and graph neural network based hierarchical graph matching for graph similarity computation. Neurocomputing 439:348–362. https://doi.org/10.1016/j.neucom.2021.01.068

    Article  Google Scholar 

  12. Morris Antonello, Sabrina Chiesurin, Stefano Ghidoni. Enhancing semantic segmentation with detection priors and iterated graph cuts for robotics. (2020). Engineering Applications of Artificial Intelligence. 90:103467. https://doi.org/10.1016/j.engappai.2019.103467

  13. Saman Babaie-Kafaki. (2019).A hybrid scaling parameter for the scaled memoryless BFGS method based on the ℓ∞ matrix norm. Journal of the Royal Statistical Society. 96(8):1595–1602. https://doi.org/10.1080/00207160.2018.1465940

  14. Lumin Yang, Jiajie Zhuang, Hongbo Fu, Xiangzhi Wei, Kun Zhou, Youyi Zheng: Semantic Sketch Segmentation with Graph Neural Networks. (2020). International Journal of Computer Mathematics. 40(3):1–13. https://doi.org/10.1145/3450284

  15. Chuanfa Chen, Changqing Yan, Yanyan Li. A robust weighted least squares support vector regression based on least trimmed squares. Neurocomputing. 168:941–946. https://doi.org/10.1016/j.neucom.2015.05.031

  16. Ye Lu, Duan Ting, Zhu Jiayi (2020) Neural network-based semantic segmentation model for robot perception of driverless vision. IET Cyber-Syst. Robot. 2(4):190–196. https://doi.org/10.1049/iet-csr.2020.0040

    Article  Google Scholar 

  17. Sang-Sik Yeom, Jong-Eun Ha. David. 3D Indoor Scene Semantic Segmentation using 2D Semantic Segmentation Projection. ournal of Institute of Control, Robotics and Systems. 26(11):949–954. https://doi.org/10.5302/j.icros.2020.20.0120.

  18. Kusno Kusno. (2020). Fitting a Curve, Cutting Surface, and Adjusting the Shapes of Developable Hermite Patches. Mathematics and Statistics .8(6):740–746. https://doi.org/10.13189/ms.2020.080615

  19. Liu K, Jin H (2020) Arm-Root Curve Fitting Based on Body Surface Feature Points for Young Male. World J. Eng. Technol. 09(02):241–249. https://doi.org/10.4236/wjet.2021.92017

    Article  Google Scholar 

  20. Ghadi DM, Adil AL-Rammahi. (2020) Improvement of Menezes-Vanstone Elliptic Curve Cryptosystem Based on Quadratic Bézier Curve Technique. J Comput Sci 16(5):715–722. https://doi.org/10.3844/jcssp.2020.715.722

    Article  Google Scholar 

  21. Wang Ningming, Wang Shuhua (2020) A calibration data curve fitting method based on matrix orthogonal triangulation. Procedia Computer Sci. 174:89–94. https://doi.org/10.1016/j.procs.2020.06.061

    Article  Google Scholar 

  22. Zerbo SG, Maestripieri A, Pería FM (2020) Indefinite Abstract Splines with a Quadratic Constraint. J Optim Theory Appl 186(1):209–225. https://doi.org/10.1007/s10957-020-01692-z

    Article  MathSciNet  MATH  Google Scholar 

  23. Raslan KR, Ali KK (2020) On n-dimensional quadratic B-splines. Numerical Methods for Partial Differential Equations 37(2):1057–1071. https://doi.org/10.1002/num.22566

    Article  MathSciNet  Google Scholar 

  24. Yan J, Patterson N, Narasimhan VM (2020) miqoGraph: fitting admixture graphs using mixed-integer quadratic optimization. Bioinformatics 37(16):2488–2490. https://doi.org/10.1093/bioinformatics/btaa988

    Article  Google Scholar 

  25. Qiao, JF., Meng, X., Li, WJ. et al. (2020).A novel modular RBF neural network based on a brain-like partition method. Neural Comput & Applic 32, 899–911 (2020). https://doi.org/10.1007/s00521-018-3763-z.

  26. Abdelaaziz Mahdaoui, El Hassan Sbai.(2020).3D Point Cloud Simplification Based on k-Nearest Neighbor and Clustering. Advances in Multimedia. 2020:1–10. https://doi.org/10.1155/2020/8825205

  27. Zhou Wu, Zeng Yan, Li DongSheng, Liu Jiepeng, Feng Liang (2021) High-volume point cloud data simplification based on decomposed graph filtering. Automation in Construction. 129:103815. https://doi.org/10.1016/j.autcon.2021.103815

    Article  Google Scholar 

  28. Li W-H, Xiang S, Nie W-Z, Song D, Liu A-A, Li X-Y, Hao T (2020) Joint deep feature learning and unsupervised visual domain adaptation for cross-domain 3D object retrieval. Inf Process Manage 57(5):102275. https://doi.org/10.1016/j.ipm.2020.102275

    Article  Google Scholar 

  29. Chao Chen, Zhihong Chen, Boyuan Jiang, Xinyu Jin.(2019).Joint Domain Alignment and Discriminative Feature Learning for Unsupervised Deep Domain Adaptation. roceedings of the AAAI Conference on Artificial Intelligence. 33:3296–3303.1609/aaai.v33i01.33013296.

Download references

Acknowledgments

The research is supported by: Hebei Province Key Research and Development Project (No.20313701D); Hebei Province Key Research and Development Project (No.19210404D); National Natural Science Foundation of China (No. U1536112); National Social Science; Foundation Key Project (No. 17AJL014); National Natural Science Foundation of China (No. 81673697); National Natural Science Foundation of China (No. 61872046); "Blue Fire Project" (Huizhou) University of Technology Joint Innovation Project (CXZJHZ201729); Industry-University Cooperation Cooperative Education Project of the Ministry of Education (No. 201902218004); Industry-University Cooperation Cooperative Education Project of the Ministry of Education (No. 201902024006); The Ministry of Education Industry-University Cooperation Collaborative Education Project (No. 201901197001); Industry-University Cooperation Cooperative Education Project of the Ministry of Education (No. 201901197007); Industry-University Cooperation Collaborative Education Project of the Ministry of Education (No. 201901199005); Educational Reform Project of Beijing University of Posts and Telecommunications (No. 500520096,No: 500519813 No: 500521171,); Special project for youth research and innovation: Beijing University of Posts and Telecommunications Project on Tuberculosis (2019 PTB-011); Supported by the Fundamental Research Funds for the Central Universities (Grant No.2019RC52).

Author information

Authors and Affiliations

  1. School of Computer Science (National Pilot Software Engineering School), Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Yi Sun

  2. International School, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Shenhu Zhang

  3. School of Economics and Management, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Tianqi Wang

  4. Institute of Quantitative & Technical Economics, Chinese Academy of Social Sciences, Beijing, 100028, China

    Feng Lou

  5. Academy of Science and Technology, Xianhe Environmental Protection Technology Joint Stock Limited Company, Hebei, 050035, China

    Jingjin Ma & Chunying Wang

  6. College of Information Engineering, Qingdao Qiushi College, Shandong, 266108, China

    Chengrong Gui

Authors
  1. Yi Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Shenhu Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Tianqi Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Feng Lou
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Jingjin Ma
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Chunying Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  7. Chengrong Gui
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yi Sun.

Ethics declarations

Conflicts of Interest

Compared with traditional segmentation or simplification algorithms, the proposed method not only reduces the sensitivity to noise data and improves the accuracy but also solves the defect of fuzzy boundary division, further overcomes the defect of inaccurate curvature weighting of target sample points, and achieves the smooth transition target of curvature of sample points.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

(See Tables 1 and 2)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, Y., Zhang, S., Wang, T. et al. An improved spatial point cloud simplification algorithm. Neural Comput & Applic 34, 12345–12359 (2022). https://doi.org/10.1007/s00521-021-06582-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-021-06582-7

Keywords