Skip to main content
Springer Nature Link
Log in

A new PDE learning model for image denoising

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

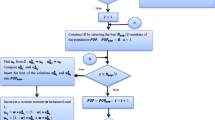
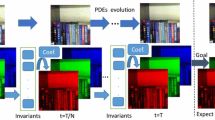
Selecting appropriate terms to design partial differential equations (PDEs) for specific processing and vision tasks have a prominent role in achieving acceptable results. In this paper, we present an automatic method to obtain a set of suitable terms of PDE for specific processing and vision tasks. Therefore, a new optimization framework has been constructed which is constrained with PDEs in the form of linear combinations of differential terms with time-independent coefficients, and is solved through training data. The optimization problem could be solved by translating it to a least square problem through the assumption of independency of time. By this assumption, it is possible to select any arbitrary term for the PDE and blend different PDEs for processing tasks, including image denoising. Several numerical experiments in image denoising prove the present model robust to the size of data and the kind of its noise.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Aubert G, Kornprobst P (2001) Mathematical Problems in Image Processing. Partial Differential Equations and the Calculus of Variations. Springer, New York

    MATH  Google Scholar 

  2. Gabor D (1965) Information theory in electron microscopy. Lab Invest 14:801–807

    Google Scholar 

  3. Koenderink J (1984) The structure of images. Biol Cybern 50:363–370

    Article  MathSciNet  Google Scholar 

  4. Perona P, Malik J (1990) Scale-space and edge detection using anisotropic diffusion. IEEE Trans Pattern Anal Mach Intell 12:629–639

    Article  Google Scholar 

  5. Catte F, Lions PL, Morel JM, Coll T (1992) Image selective smoothing and edge detection by nonlinear diffusion. SIAM J Numer Anal 29:845–866

    Article  MathSciNet  Google Scholar 

  6. Weickert J (1999) Coherence-enhancing diffusion filtering. Int J Comput Vis 31:111–127

    Article  Google Scholar 

  7. Weickert J (1998) Anisotropic diffusion in image processing. University of Copenhagen Denmark Press

  8. Rudin L, Osher S, Fatemi E (1992) Nonlinear total variation based noise removal algorithms. Phys D 60:259–268

    Article  MathSciNet  Google Scholar 

  9. Chan TF, Golub GH, Mulet P (1999) A nonlinear primal-dual method for total variation based image restoration. SIAM J Sci Comput 20:1964–1977

    Article  MathSciNet  Google Scholar 

  10. Chan T, Esedoglu S (2005) Aspects of total variation regularized L1 function approximation. SIAM J Multiscale Model Simul 65:1817–1837

    MATH  Google Scholar 

  11. Gilboa G, Soche N, Zeevi Y (2006) Variational denoising of partly textured images by spatially varying constraints. IEEE Trans Image Process 15:2281–2289

    Article  Google Scholar 

  12. Aubert G, Vese LA (1997) A variational method in image recovery. SIAM J Numer Anal 34:1948–1979

    Article  MathSciNet  Google Scholar 

  13. Li W, Li Q, Gong W (2012) Total variation blind deconvolution employing split Bregman iteration. J Vis Commun Image Represent 23:409–417

    Article  Google Scholar 

  14. Wang Y, Chen WF, Zhou SJ (2011) MTV: modified total variation model for image noise removal. IEE Electron Device Lett. 47:592–594

    Article  Google Scholar 

  15. Li F, Shen C, Liu R, Fan J (2011) A fast implementation algorithm of TV inpainting model based on operator splitting method. Comput Electr Eng 37:782–788

    Article  Google Scholar 

  16. Chan T, Marquina A, Mulet P (2000) High order total variation-based image restoration. SIAM J Sci Comput 22:503–516

    Article  MathSciNet  Google Scholar 

  17. Lysaker M, Osher S, Tai XC (2004) Noise removal using smoothed normals and surface fitting. IEEE Trans Image Process 13:1345–57

    Article  MathSciNet  Google Scholar 

  18. Lysaker M, Lundervold A, Tai XC (2003) Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time. IEEE Trans Image Process 12:1579–1590

    Article  Google Scholar 

  19. Lysaker M, Tai XC (2006) Iterative image restoration combining total variation minimization and a second-order functional. Int J Comput Vis 66:5–18

    Article  Google Scholar 

  20. Blomgren P, Chan TF, Mulet P (1997) Extensions to total variation denoising. In: Proceedings society of photo-optical instrumentation engineers SPIE, San Diego

  21. Jidesh P, George S (2012) Shock coupled fourth-order diffusion for image enhancement. Comput Electr Eng 38:1262–1277

    Article  Google Scholar 

  22. Li F, Shen C, Fan J (2007) Image restoration combining a total variational filter and a fourth-order filter. J Vis Commun Image Represent 18:322–330

    Article  Google Scholar 

  23. Wang H, Wang Y, Ren W (2012) Image denoising using anisotropic second and fourth order diffusions based on gradient vector convolution. Comput Sci Inf Syst 9:1493–1511

    Article  Google Scholar 

  24. You YL, Kaveh M (2000) Fourth-order partial differential equations for noise removal. IEEE Trans Image Process 9:1723–1730

    Article  MathSciNet  Google Scholar 

  25. Liu R, Lin Z, Zhang W, Su Z (2010) Learning PDEs for image restoration via optimal control. In: European conference on computer vision, 115–128

  26. Lin Z, Zhang W, Tang X (2008) Learning partial differential equations for computer vision. Technical report, Microsoft Research

  27. Liu R, Lin Z, Zhang W, Tang K, Su Z (2013) Toward designing intelligent PDEs for computer vision: an optimal control approach. Image Vis Comput 31:43–56

    Article  Google Scholar 

  28. Zhao Z, Jiaoy Y, Hou C, Wu Y (2016) Learning partial differential equations for saliency detection. In: IEEE international conference on big data analysis (ICBDA)

  29. Jiao Y, Pan X, Zhao Z, Hou C (2018) Learning sparse partial differential equations for vector-valued images. Neural Comput Appl 29:120–1216

    Article  Google Scholar 

  30. Fang C, Zhao Z, Zhou P, Lin Z (2017) Feature learning via partial differential equation with applications to face recognition. Pattern Recogn 69:14–25

    Article  Google Scholar 

  31. Moorthi S, Karthikeyan S (2018) A study on learning partial differential equations algorithm for face recognition. Int J Innov Res 5:2347–6060

    Google Scholar 

  32. Tikhonov AN, Arsenin VY (1977) Solutions of ill-posed problems. Winston and Sons, Washington

    MATH  Google Scholar 

  33. Aubert G, Vese L (1997) A variational method in image recovery. SIAM J Numer Anal 34:1948–1979

    Article  MathSciNet  Google Scholar 

  34. Vese L (1996) Problemes variationals et EDP pour lanalyse dimages et levolution de courbes. PhD thesis, Universite de Nice Sophia-Antipolis

  35. Olver P (1993) Applications of lie groups to differential equations. Springer

  36. Kim D, Fessler JA (2016) Optimized first-order methods for smooth convex minimization. Math Prog 151:81–107

    Article  MathSciNet  Google Scholar 

  37. Gabay D, Mercier B (1976) A dual algorithm for the solution of nonlinear variational problems via finite-element approximations. Camput Math Appl 2:17–40

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the anonymous reviewers for their useful suggestions and valuable comments which were greatly helpful to improve the quality of this paper.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Faculty of Mathematical Sciences, Tarbiat Modares University, P.O. Box 14115-134, Tehran, Iran

    F. Ashouri & M. R. Eslahchi

Authors
  1. F. Ashouri
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. M. R. Eslahchi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to M. R. Eslahchi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ashouri, F., Eslahchi, M.R. A new PDE learning model for image denoising. Neural Comput & Applic 34, 8551–8574 (2022). https://doi.org/10.1007/s00521-021-06620-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-021-06620-4

Keywords