Skip to main content
Springer Nature Link
Log in

RFIS: regression-based fuzzy inference system

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

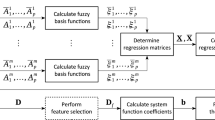
This paper proposes a new multivariable fuzzy inference system without explicitly defined fuzzy rules. This system uses Gaussian fuzzy sets for the inputs and linearly and nonlinearly parameterized system functions. To determine their parameters, linear and nonlinear regressions are used. The linear regression is realized by the ridge regression and the nonlinear regression by the Levenberg–Marquardt algorithm. The input fuzzy sets are determined by a multi-objective genetic algorithm with a feature selection method. In the case of linearly parameterized system functions, the following methods are considered: F-test, ReliefF, a regression tree, neighborhood component analysis, and lasso regression. In the case of nonlinearly parameterized system functions, terms from the so-called term matrix are coded in an individual, and they are selected by using a genetic algorithm. In the paper, two pairs of objective functions are defined: one pair, consisting of the number of active predictors and the root of the mean squared error, for constructing fuzzy estimators, and the second pair, consisting of the number of active predictors and confusion values, for constructing fuzzy classifiers. These multi-criteria objective functions enable the selection of models from the Pareto fronts taking into account the compromise between model accuracy and its simplification. The proposed method was tested on four examples: approximation of a one-variable function, two-class classification of banknotes, prediction of a time series, and prediction of automobile fuel consumption. The conducted experiments confirmed the usefulness of the proposed solution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability Statement

All experiments were carried out on publicly available data sets.

References

  1. Aghaeipoor F, Javidi MM (2019) MOKBL+MOMs: an interpretable multi-objective evolutionary fuzzy system for learning high-dimensional regression data. Inform Sci 496:1–24. https://doi.org/10.1016/j.ins.2019.04.035

    Article  Google Scholar 

  2. Aydogan EK, Karaoglan I, Pardalos PM (2012) HGA: hybrid genetic algorithm in fuzzy rule-based classification systems for high-dimensional problems. Appl Soft Comput J 12(2):800–806. https://doi.org/10.1016/j.asoc.2011.10.010

    Article  Google Scholar 

  3. BIMK Group (2022) PlatEMO evolutionary multi-objective optimization platform user manual 3:4

  4. Chen SM, Hsin WC (2015) Weighted fuzzy interpolative reasoning based on the slopes of fuzzy sets and particle swarm optimization techniques. IEEE Trans Cybern 45(7):1250–1261. https://doi.org/10.1109/TCYB.2014.2347956

    Article  Google Scholar 

  5. Dhiman G, Singh KK, Slowik A, Chang V, Yildiz AR, Kaur A, Garg M (2021) EMoSOA: a new evolutionary multi-objective seagull optimization algorithm for global optimization. Int J Mach Learn Cybern 12(2):571–596. https://doi.org/10.1007/s13042-020-01189-1

    Article  Google Scholar 

  6. Dua D, Graff C (2021) UCI machine learning repository. http://archive.ics.uci.edu/ml

  7. Gu ZM, Wang GG (2020) Improving nsga-iii algorithms with information feedback models for large-scale many-objective optimization. Future Gener Comput Syst 107:49–69. https://doi.org/10.1016/j.future.2020.01.048

    Article  Google Scholar 

  8. Güven MK, Passino KM (2001) Avoiding exponential parameter growth in fuzzy systems. IEEE Trans Fuzzy Syst 9(1):194–199. https://doi.org/10.1109/91.917125

    Article  Google Scholar 

  9. Hoerl AE, Kennard RW (1970) Ridge regression: biased estimation for nonorthogonal problems. Technometrics 12(1):55–67

    Article  Google Scholar 

  10. Holland JH (1992) Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. MIT Press, USA

    Book  Google Scholar 

  11. Isfahani MK, Zekri M, Marateb HR, Mañanas MA (2019) Fuzzy jump wavelet neural network based on rule induction for dynamic nonlinear system identification with real data applications. PLoS ONE 14(12):1–26. https://doi.org/10.1371/journal.pone.0224075

    Article  Google Scholar 

  12. Jang JR (1993) ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans Syst, Man, Cybern 23(3):665–685. https://doi.org/10.1109/21.256541

    Article  Google Scholar 

  13. Li C, Wu T (2011) Adaptive fuzzy approach to function approximation with PSO and RLSE. Expert Syst Appl 38(10):13266–13273

    Article  Google Scholar 

  14. Lin L, Guo F, Xie X, Luo B (2015) Novel adaptive hybrid rule network based on TS fuzzy rules using an improved quantum-behaved particle swarm optimization. Neurocomputing 149:1003–1013. https://doi.org/10.1016/j.neucom.2014.07.033

    Article  Google Scholar 

  15. Liu Z, Chen CL, Zhang Y, Xiong LH (2012) Type-2 hierarchical fuzzy system for high-dimensional data-based modeling with uncertainties. Soft Comput 16(11):1945–1957. https://doi.org/10.1007/s00500-012-0867-8

    Article  Google Scholar 

  16. Lughofer E, Nikzad-Langerodi R (2020) Robust generalized fuzzy systems training from high-dimensional time-series data using local structure preserving PLS. IEEE Trans Fuzzy Syst 28(11):2930–2943. https://doi.org/10.1109/TFUZZ.2019.2945535

    Article  Google Scholar 

  17. Maghawry A, Hodhod R, Omar Y, Kholief M (2021) An approach for optimizing multi-objective problems using hybrid genetic algorithms. Soft Comput 25(1):389–405. https://doi.org/10.1007/s00500-020-05149-3

    Article  Google Scholar 

  18. Márquez AA, Márquez FA, Roldán AM, Peregrín A (2013) An efficient adaptive fuzzy inference system for complex and high dimensional regression problems in linguistic fuzzy modelling. Knowledge-Based Syst 54:42–52. https://doi.org/10.1016/j.knosys.2013.05.012

    Article  Google Scholar 

  19. Mellal MA, Salhi A (2021) Multi-objective system design optimization via PPA and a fuzzy method. Int J Fuzzy Syst 23(5):1213–1221. https://doi.org/10.1007/s40815-021-01068-z

    Article  Google Scholar 

  20. Novakovic BM (1999) Fuzzy logic control synthesis without any rule base. IEEE Trans Syst, Man, Cybern, Part B: Cybern 29(3):459–466. https://doi.org/10.1109/3477.764883

    Article  Google Scholar 

  21. Seber G, Wild C (2005) Nonlinear regression. Wiley Series in Probability and Statistics Wiley, Hoboken

    MATH  Google Scholar 

  22. Singh S, Singh S, Banga VK (2020) Design of fuzzy logic system framework using evolutionary techniques. Soft Comput 24(6):4455–4468. https://doi.org/10.1007/s00500-019-04207-9

    Article  Google Scholar 

  23. Sun J, Miao Z, Gong D, Zeng XJ, Li J, Wang G (2020) Interval multiobjective optimization with memetic algorithms. IEEE Trans Cybern 50(8):3444–3457. https://doi.org/10.1109/TCYB.2019.2908485

    Article  Google Scholar 

  24. Sun TY, Tsai SJ, Tsai CH, Huo CL, Liu CC (2008) Nonlinear function approximation based on least Wilcoxon Takagi-Sugeno fuzzy model. In: 2008 Eighth International Conference on Intelligent Systems Design and Applications, 1, pp. 312–317

  25. Tak N, Evren AA, Tez M, Egrioglu E (2018) Recurrent type-1 fuzzy functions approach for time series forecasting. Appl Intell 48(1):68–77. https://doi.org/10.1007/s10489-017-0962-8

    Article  Google Scholar 

  26. Takagi T, Sugeno M (1985) Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern 1:116–132. https://doi.org/10.1109/TSMC.1985.6313399

    Article  MATH  Google Scholar 

  27. The MathWorks Inc (2020) Fuzzy Logic Toolbox User’s Guide. Natick, Massachusetts, United States

  28. The MathWorks Inc (2020) Global Optimization Toolbox User’s Guide. Natick, Massachusetts, United States

  29. The MathWorks Inc (2020) Statistics and machine learning Toolbox User’s Guide. Natick, Massachusetts, United States

  30. The MathWorks Inc (2021) Fuzzy Logic Toolbox User’s Guide. Natick, Massachusetts, United States

  31. Tian Y, Cheng R, Zhang X, Jin Y (2017) PlatEMO: a MATLAB platform for evolutionary multi-objective optimization. IEEE Comput Intell Mag 12(4):73–87

    Article  Google Scholar 

  32. Unal AN, Kayakutlu G (2020) Multi-objective particle swarm optimization with random immigrants. Complex Intell Syst 6(3):635–650. https://doi.org/10.1007/s40747-020-00159-y

    Article  Google Scholar 

  33. Wang LX, Mendel J (1992) Generating fuzzy rules by learning from examples. IEEE Trans Syst Man Cybern 22(6):1414–1427. https://doi.org/10.1109/21.199466

    Article  MathSciNet  Google Scholar 

  34. Wang S, Chung KFL, Lu J, Han B, Hu D (2004) Fuzzy inference systems with no any rule base and linearly parameter growth. J Control Theory Appl 2(2):185–192. https://doi.org/10.1007/s11768-004-0067-x

    Article  MathSciNet  Google Scholar 

  35. Whitley DCSU (1994) A genetic algorithm tutorial by Darrell Whitley. Statist Comput 2(4):65–85. https://doi.org/10.1007/BF00175354

    Article  Google Scholar 

  36. Wiktorowicz K, Krzeszowski T (2020) Approximation of two-variable functions using high-order Takagi-Sugeno fuzzy systems, sparse regressions, and metaheuristic optimization. Soft Comput 24:1–15. https://doi.org/10.1007/s00500-020-05238-3

    Article  Google Scholar 

  37. Wiktorowicz K, Krzeszowski T (2020) Training High-Order Takagi-Sugeno fuzzy systems using batch least squares and particle swarm optimization. Int J Fuzzy Syst 22(1):22–34. https://doi.org/10.1007/s40815-019-00747-2

    Article  Google Scholar 

  38. Yang YK, Sun TY, Huo CL, Yu YH, Liu CC, Tsai CH (2013) A novel self-constructing radial basis function neural-fuzzy system. Appl Soft Comput 13(5):2390–2404

    Article  Google Scholar 

  39. Yi JH, Xing LN, Wang GG, Dong J, Vasilakos AV, Alavi AH, Wang L (2020) Behavior of crossover operators in nsga-iii for large-scale optimization problems. Inform Sci 509:470–487. https://doi.org/10.1016/j.ins.2018.10.005

    Article  MathSciNet  Google Scholar 

  40. Zhang Y, Wang GG, Li K, Yeh WC, Jian M, Dong J (2020) Enhancing moea/d with information feedback models for large-scale many-objective optimization. Inform Sci 522:1–16. https://doi.org/10.1016/j.ins.2020.02.066

    Article  MathSciNet  MATH  Google Scholar 

  41. Zhao L, Qian F, Yang Y, Zeng Y, Su H (2010) Automatically extracting T-S fuzzy models using cooperative random learning particle swarm optimization. Appl Soft Comput 10(3):938–944. https://doi.org/10.1016/j.asoc.2009.10.012

    Article  Google Scholar 

Download references

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. Faculty of Electrical and Computer Engineering, Rzeszow University of Technology, al. Powstancow Warszawy 12, 35-959, Rzeszow, Poland

    Krzysztof Wiktorowicz

Authors
  1. Krzysztof Wiktorowicz
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Krzysztof Wiktorowicz.

Ethics declarations

Conflicts of interest

Not applicable.

Code availability

The MATLAB code is available at: https://www.mathworks.com/matlabcentral/fileexchange/95848-rfis-regression-based-fuzzy-inference-system.

Ethical approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wiktorowicz, K. RFIS: regression-based fuzzy inference system. Neural Comput & Applic 34, 12175–12196 (2022). https://doi.org/10.1007/s00521-022-07105-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07105-8

Keywords