Skip to main content

Advertisement

Springer Nature Link
Log in

Automatic fuzzy clustering for probability density functions using the genetic algorithm

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

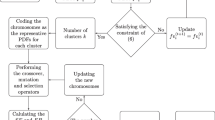
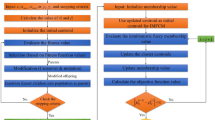
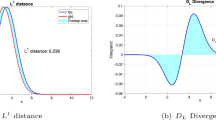
Based on the genetic algorithm, this study develops the new fuzzy clustering method for probability density functions (pdfs) with the important improvements. First, the \(L^1\)-distance is proposed as the measure to evaluate the level similar of the pdfs. It is surveyed to find the bounds and established the methods to compute. Second, we propose the new objective for the genetic algorithm. This objective measures both the similarity of elements in each group and the quality of clustering. Finally, the operators such as crossover, mutation, and selection of the traditional genetic algorithm are improved. Combining these improvements, we have an efficient cluster analysis algorithm for pdfs. In this algorithm, the proper number of groups, the specific pdfs in each cluster, and the fuzzy relationship between the pdf to the established clusters are determined at the same time. The convergence of the proposed algorithm is proved by theory and performed by the established MATLAB program. The experiments and applications show superiority of the developed algorithm in comparing to the existing algorithms. The proposed algorithm is also applied in recognizing images to certify the feasibility and applicability of the studied problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+
from $39.99 /Month
  • Starting from 10 chapters or articles per month
  • Access and download chapters and articles from more than 300k books and 2,500 journals
  • Cancel anytime
View plans

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Hubert L, Arabie P (1985) Comparing partitions. J Classif 2(1):193–218

    Article  MATH  Google Scholar 

  2. Nguyentrang T, Vovan T (2017) Fuzzy clustering of probability density functions. J Appl Stat 44(4):583–601

    Article  MathSciNet  MATH  Google Scholar 

  3. Cabanes G, Bennani Y, Destenay R, Hardy A (2013) A new topological clustering algorithm for interval data. Pattern Recognit 46(11):3030–3039

    Article  Google Scholar 

  4. Chen J-H, Hung W-L (2015) An automatic clustering algorithm for probability density functions. J Stat Comput Simul 85(15):3047–3063

    Article  MathSciNet  MATH  Google Scholar 

  5. Goh A, Vidal R (2008) Clustering and dimensionality reduction on Riemannian manifolds. In: 2008 IEEE conference on computer vision and pattern recognition. IEEE, pp 1–7

  6. VoVan T, NguyenTrang T (2018) Similar coefficient for cluster of probability density functions. Commun Stat Theory Methods 47(8):1792–1811

    Article  MathSciNet  MATH  Google Scholar 

  7. VoVan T, Trang TN (2018) Similar coefficient of cluster for discrete elements. Sankhya B 80(1):19–36

    Article  MathSciNet  MATH  Google Scholar 

  8. Bezdek JC (1980) A convergence theorem for the fuzzy isodata clustering algorithms. IEEE Trans Pattern Anal Mach Intell 1:1–8

    Article  MATH  Google Scholar 

  9. Bora DJ, Gupta AK (2014) Impact of exponent parameter value for the partition matrix on the performance of fuzzy c means algorithm. arXiv preprint arXiv:1406.4007

  10. Jain M, Vayada MG (2017) Non-cognitive color and texture based image segmentation amalgamation with evidence theory of crop images. In: 2017 third international conference on sensing, signal processing and security (ICSSS). IEEE, pp 160–165

  11. Vovan T, Nguyen-Thoi T, Vo-Duy T, Ho-Huu V, Nguyen-Trang T (2017) Modified genetic algorithm-based clustering for probability density functions. J Stat Comput Simul 87(10):1964–1979

    Article  MathSciNet  MATH  Google Scholar 

  12. Vovan T (2017) L 1-distance and classification problem by Bayesian method. J Appl Stat 44(3):385–401

    Article  MathSciNet  MATH  Google Scholar 

  13. Phamtoan D, Vovan T, Pham-Chau A, Nguyen-Trang T, Ho-Kieu D (2019) A new binary adaptive elitist differential evolution based automatic k-medoids clustering for probability density functions. Math Probl Eng 2019:4528

    Google Scholar 

  14. Montanari A, Calò DG (2013) Model-based clustering of probability density functions. Adv Data Anal Classif 7(3):301–319

    Article  MathSciNet  MATH  Google Scholar 

  15. Matusita K (1967) On the notion of affinity of several distributions and some of its applications. Ann Inst Stat Math 19(1):181

    Article  MathSciNet  MATH  Google Scholar 

  16. Pham-Gia T, Turkkan N, Vovan T (2008) The maximum function in statistical discrimination analysis. Commun Stat Simul Comput 37:320–336

    Article  MATH  Google Scholar 

  17. Glick N (1973) Separation and probability of correct classification among two or more distributions. Ann Inst Stat Math 25(1):373–382

    Article  MathSciNet  MATH  Google Scholar 

  18. Vovan T, Pham-Gia T (2010) Clustering probability distributions. J Appl Stat 37(11):1891–1910

    Article  MathSciNet  MATH  Google Scholar 

  19. Vovan T, Phamtoan D, Tranthituy D (2019) Automatic genetic algorithm in clustering for discrete elements. Commun Stat Simul Comput 56:1–16

    MATH  Google Scholar 

  20. Holland JH (1973) Genetic algorithms and the optimal allocation of trials. SIAM J Comput 2(2):88–105

    Article  MathSciNet  MATH  Google Scholar 

  21. Bandyopadhyay S, Maulik U (2001) Nonparametric genetic clustering: comparison of validity indices. IEEE Trans Syst Man Cybern C 31(1):120–125

    Article  Google Scholar 

  22. Bandyopadhyay S, Maulik U (2002) Genetic clustering for automatic evolution of clusters and application to image classification. Pattern Recognit 35(6):1197–1208

    Article  MATH  Google Scholar 

  23. Vovan T (2019) Cluster width of probability density functions. Intell Data Anal 23(2):385–405

    Article  MathSciNet  Google Scholar 

  24. Lai C-C (2005) A novel clustering approach using hierarchical genetic algorithms. Intell Autom Soft Comput 11(3):143–153

    Article  Google Scholar 

  25. Kamel MS, Selim SZ (1994) New algorithms for solving the fuzzy clustering problem. Pattern Recognit 27(3):421–428

    Article  Google Scholar 

  26. Bazaraa MS, Sherali HD (2013) Shetty CM nonlinear programming: theory and algorithms. Wiley, New York

    Google Scholar 

  27. Golilarz NA, Demirel H, Gao H (2019) Adaptive generalized gaussian distribution oriented thresholding function for image de-noising. Int J Adv Comput Sci Appl 10(2):10–15

    Google Scholar 

  28. Deep K, Singh KP, Kansal ML, Mohan C (2009) A real coded genetic algorithm for solving integer and mixed integer optimization problems. Appl Math Comput 212(2):505–518

    MathSciNet  MATH  Google Scholar 

  29. Diem HK, Trung VD, Trung NT, Vovan T, Thao NT (2018) A differential evolution-based clustering for probability density functions. IEEE Access 6:41325–41336

    Article  Google Scholar 

  30. Xu X, Li X, Liu X, Shen H, Shi Q (2016) Multimodal registration of remotely sensed images based on Jeffrey’s divergence. ISPRS J Photogramm Remote Sens 122:97–115

    Article  Google Scholar 

  31. Grogan M, Dahyot R (2019) L2 divergence for robust colour transfer. Comput Vis Image Underst 181:39–49

    Article  Google Scholar 

Download references

Acknowledgements

This research is funded by Ministry of Education and Training in Viet Nam under Grant Number: B2022-TCT–03.

Author information

Authors and Affiliations

  1. University of Science, Ho Chi Minh City, Vietnam

    Dinh Phamtoan

  2. Vietnam National University, Ho Chi Minh City, Vietnam

    Dinh Phamtoan

  3. Faculty of Mechanical, Electrical and Computer Engineering, School of Engineering and Technology, Van Lang University, Ho Chi Minh City, Vietnam

    Dinh Phamtoan

  4. College of Natural Science, Can Tho University, Can Tho City, Vietnam

    Tai Vovan

Authors
  1. Dinh Phamtoan
    View author publications

    Search author on:PubMed Google Scholar

  2. Tai Vovan
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Tai Vovan.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

See Fig. 16.

Fig. 16
figure 16figure 16

The convergence of 100 pdfs in the first stages

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Phamtoan, D., Vovan, T. Automatic fuzzy clustering for probability density functions using the genetic algorithm. Neural Comput & Applic 34, 14609–14625 (2022). https://doi.org/10.1007/s00521-022-07265-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07265-7

Keywords

Profiles

  1. Tai Vovan View author profile