Evolving topology and weights of specialized and non-specialized neuro-controllers for robot motion in various environments

Abstract

This paper deals with the topology and weight evolution of Neuro-Controllers (NCs). It focuses on meta-problems of developing motion controllers that can operate successfully in several given motion-problems, where each of these motion problems defers by the arena and task. Here, the evolution aims to find both specialized and non-specialized controllers. The non-specialized controllers are evolved to provide a successful motion for the entire set of the given motion-problems, whereas each specialized controller is evolved to be optimal in at least one of these problems. The meta-problem is defined as a many-objective optimization problem, in which the kth objective is to maximize the motion performance in the kth motion problem. Following the problem description, a decomposition-based evolutionary algorithm, which is termed NEWS/D, is presented. This algorithm, which has recently been proposed by the authors, is specially designed to allow the topology and weight evolution of NCs under a large number of objectives. Next, the algorithm is applied to find NCs for three meta-problems, i.e., three sets of motion problems. The results of the experiments show that the obtained three sets of NCs include both specialized and non-specialized controllers. In addition, the proposed approach of many-objective topology and weight evolution of NCs is analyzed in comparison with other approaches, including three versions of decomposition-based fixed topology optimization. It is shown here that for the same number of evaluations, NEWS/D achieved better results than those of the other approaches. Finally, a topology analysis is carried out for the specialized NCs, which suggests that the solution includes multiple equivalent NCs. The numerical implications of this phenomenon are left for future work.

Appendix

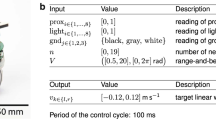
The robot’s model is a two-wheel-driven mobile robot as in [43]. Eight sensor modules have been simulated. Each module includes a single target range sensor and a single obstacle range sensor. The modules are equally spaced around the robot’s body. The sensor's characteristics are the same for all sensors of the same type. The maximum sensing range of the obstacle sensors is 5 cm with a beam width span of 6°. The maximum sensing range of the target sensors is 100 cm with a beam width span of 30°. The sensor's output is a value within the range [0, 1], where 1 is the value for objects located at the maximum sensing range (and beyond) and 0 is the value for touching the object. All the sensors are ideal with no sensor noise considered. The robot’s motion is defined as follows. At each control-time-step ${\Delta }t_{{{\text{step}}}}$, the robot’s controller receives signals from the simulated sensors as a real-numbered vector, ${\varvec{In}} \in {\mathbb{R}}^{16}$. Based on these signals, the controller generates motor commands, ${{\varvec{\Omega}}}^{{\text{T}}} = \left[ {\omega_{R} ,\omega_{L} } \right]^{T}$. These commands are applied as rotational velocity for the left ($\omega_{L}$) and the right ($\omega_{R}$) motors. During ${\Delta }t_{{{\text{step}}}}$, in each simulation-time-step, ${\text{d}}t \ll \Delta t_{{{\text{step}}}}$, the robot location is updated according to Eqs. (12) and (13).

$$\left\{ {\begin{array}{*{20}l} {v_{x} \left( t \right) = \frac{{R_{w} }}{2} \cdot \left( {\omega_{R} + \omega_{L} } \right)\cos \phi \left( t \right)} \hfill \\ {v_{y} \left( t \right) = \frac{{R_{w} }}{2} \cdot \left( {\omega_{R} + \omega_{L} } \right)\sin \phi \left( t \right)} \hfill \\ {v_{\phi } \left( t \right) = \frac{{R_{w} }}{{D_{R} }}\left( {\omega_{R} - \omega_{L} } \right)} \hfill \\ \end{array} } \right.$$

(12)

$$\left\{ {\begin{array}{*{20}c} {x\left( {t + {\text{d}}t} \right) = x\left( t \right) + v_{x} \left( t \right) \cdot {\text{d}}t} \\ {y\left( {t + {\text{d}}t} \right) = y\left( t \right) + v_{y} \left( t \right) \cdot {\text{d}}t} \\ {\phi \left( {t + {\text{d}}t} \right) = \phi \left( t \right) + v_{\phi } \left( t \right) \cdot {\text{d}}t} \\ \end{array} } \right.$$

(13)

where $v_{x} \left( t \right)$ and $v_{y} \left( t \right)$ are the robot's center horizontal and vertical velocity, respectively. Also, $v_{\phi } \left( t \right)$ is the robot's angular velocity. $R_{w}$ is the radius of the robot wheels, $D_{R}$ is the distance between the robots’ wheels. $\left[ {x\left( t \right),y\left( t \right)} \right]$ are the current horizontal and vertical coordinates of the robot in the motion-problem system, whereas $\left[ {x\left( {t + {\text{d}}t} \right),y\left( {t + {\text{d}}t} \right)} \right]$ present the updated coordinates. $\phi \left( t \right)$ presents the robot's orientation and $\phi \left( {t + {\text{d}}t} \right)$ presents the updated orientation. Here, the orientation is defined by the angle between the robot axis and the horizontal axis of the motion-problem coordinate system. The parameters ${\Delta }t_{{{\text{step}}}} = 5,\;{\text{d}}t = 0.01,\;D_{R} = 5.5\;{\text{cm}},\;R_{w} = 1\;{\text{cm}}$ are used in this experimental study. Figure 

Fig. 10

Control schemes

10 provides a block diagram for the neuro-control scheme of the robot. It should be noted that the NC receives signals from the sensors without any pre-defined knowledge of the sensor type or the robot location.