Skip to main content

Advertisement

Springer Nature Link
Log in

The application of Bayesian model averaging based on artificial intelligent models in estimating multiphase shock flood waves

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

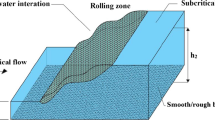
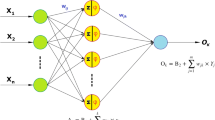
The multiphase shock wave phenomenon is significantly affected by accumulated upstream sediment deposition and downstream hydraulic conditions. There is a lack of studies evaluating the efficacy of intelligent models in representing multiphase debris flooding over initially dry- or wet-bed tail-waters, or over downstream semi-circular obstacles. To address this, we propose a novel methodology based on Bayesian Model Averaging (BMA), which combines predictions of three individual intelligent models [i.e., “Multi-layer Perceptron” (MLP), “Generalized Regression Neural Network”, and “Support Vector Regression”]. The models were developed through experimental study whereupon high-quality sediment depths and water levels data (n = 9000) were collected from 18 shock wave scenarios with various initial conditions in channel up- and down-stream. Experimental data and related original videos are created accessible in an online repository may be used in other researches. Each model’s results were in close concord with the experimental data; RMRE and RMSE values were in the range of 1.54–5.99 mm and 1.21–40.49 mm, respectively (0.5–2% and 0.4–13.5%) with the MLP model marginally outperforming the other intelligent models. Based on statistical error indices, the BMA model had the best performance (up to 40% better) in estimating most data classes, and was more efficient than the best intelligent model signifying that the proposed methodology is explicit, straightforward, and promising for real-world applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Availability of data and materials

All data, produced and used during the study are available online in a public repository or appear in the submitted article [49,50,51,52].

Abbreviations

BMA:

Bayesian model averaging

MLP:

Multi-layer perceptron

GRNN:

Generalized regression neural network

SVR:

Support vector regression

CFD:

Computational fluid dynamic

ANN:

Artificial neural network

RMSE:

Root mean square error

RMRE:

Root mean relative error

RMSRE:

Root mean square relative error

NSE:

Nash–Sutcliffe efficiency coefficient

SI:

Scatter Index

R 2 :

Coefficient of determination

U S :

Initial depth of sediment in the reservoir

D W :

Initial level of water in downstream bed

T :

Time elapsed after the dam breaks

L :

Distances from reservoir beginning

R :

Radius of a semi-circular obstacle

S d :

Sediment depth

W L :

Water level

H 0 :

Initial height of the water in reservoir

\({M}_{i}\) :

Measured experimental data

\({E}_{i}\) :

Estimated values

\(\overline{M }\) :

Average of measured experimental data

\(\overline{E }\) :

Average of estimated values

\(\beta\) :

Model’s weight

\(\sigma\) :

Model’s standard deviation

\({P}_{i}\) :

A deterministic weighted average prediction

k :

Individual models

\({f}_{k}\) :

Estimation distribution of a model member

References

  1. Duarte R, Ribeiro J, Boillat JL, Schleiss A (2011) Experimental study on dam-break waves for silted-up reservoirs. J Hydraul Eng. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000444

    Article  Google Scholar 

  2. Kamra MM, Al Salami J, Sueyoshi M, Hu C (2019) Experimental study of the interaction of dambreak with a vertical cylinder. J Fluids Struct. https://doi.org/10.1016/j.jfluidstructs.2019.01.015

    Article  Google Scholar 

  3. Shi H, Si P, Dong P, Yu X (2019) A two-phase SPH model for massive sediment motion in free surface flows. Adv Water Resour 129:80–98. https://doi.org/10.1016/j.advwatres.2019.05.006

    Article  Google Scholar 

  4. Issakhov A, Imanberdiyeva M (2019) Numerical simulation of the movement of water surface of dam break flow by VOF methods for various obstacles. Int J Heat Mass Transf. https://doi.org/10.1016/j.ijheatmasstransfer.2019.03.034

    Article  MATH  Google Scholar 

  5. Issakhov A, Zhandaulet Y, Nogaeva A (2018) Numerical simulation of dam break flow for various forms of the obstacle by VOF method. Int J Multiph Flow. https://doi.org/10.1016/j.ijmultiphaseflow.2018.08.003

    Article  MathSciNet  Google Scholar 

  6. Ye Z, Zhao X (2017) Investigation of water-water interface in dam break flow with a wet bed. J Hydrol. https://doi.org/10.1016/j.jhydrol.2017.02.055

    Article  Google Scholar 

  7. Wang X, Chen W, Zhou Z, Zhu Y, Wang C, Liu Z (2017) Three-dimensional flood routing of a dam break based on a high-precision digital model of a dense urban area. Nat Hazards. https://doi.org/10.1007/s11069-016-2734-x

    Article  Google Scholar 

  8. He Z, Wu T, Weng H, Hu P, Wu G (2017) Numerical simulation of dam-break flow and bed change considering the vegetation effects. Int J Sediment Res. https://doi.org/10.1016/j.ijsrc.2015.04.004

    Article  Google Scholar 

  9. Marsooli R, Wu W (2015) Three-dimensional numerical modeling of dam-break flows with sediment transport over movable beds. J Hydraul Eng. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000947

    Article  Google Scholar 

  10. Kim B, Sanders BF (2016) Dam-break flood model uncertainty assessment: case study of extreme flooding with multiple dam failures in Gangneung, South Korea. J Hydraul Eng. https://doi.org/10.1061/(ASCE)HY.1943-7900.0001097

    Article  Google Scholar 

  11. Lal AMW, Moustafa MZ (2016) Dam-break wave fronts in vegetated wetlands. In: World Environment Water Resource Congress 2016 Hydraulic Waterw. Hydro-Climate/Climate Change-Paper from Sess. Proceedings 2016 World Environment Water Resource Congress. https://doi.org/10.1061/9780784479872.012

  12. Seyedashraf O, Rezaei A, Akhtari AA (2017) Dam break flow solution using artificial neural network. Ocean Eng. https://doi.org/10.1016/j.oceaneng.2017.07.002

    Article  Google Scholar 

  13. Seyedashraf O, Mehrabi M, Akhtari AA (2018) Novel approach for dam break flow modeling using computational intelligence. J Hydrol. https://doi.org/10.1016/j.jhydrol.2018.03.001

    Article  Google Scholar 

  14. Soares Frazão S, Zech Y (2002) Dam break in channels with 90°bend. J Hydraul Eng. https://doi.org/10.1061/(ASCE)0733-9429(2002)128:11(956)

    Article  Google Scholar 

  15. Xue Y, Xu WL, Luo SJ, Chen HY, Li NW, Xu LJ (2011) Experimental study of dam-break flow in cascade reservoirs with steep bottom slope. J Hydrodyn. https://doi.org/10.1016/S1001-6058(10)60140-0

    Article  Google Scholar 

  16. Fraccarollo L, Toro EF (1995) Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. J Hydraul Res. https://doi.org/10.1080/00221689509498555

    Article  Google Scholar 

  17. Bellos CV, Soulis V, Sakkas JG (1992) Experimental investigation of two-dimensional dam-break induced flows. J Hydraul Res. https://doi.org/10.1080/00221689209498946

    Article  Google Scholar 

  18. Leal JGAB, Ferreira RML, Cardoso AH (2009) Maximum level and time to peak of dam-break waves on mobile horizontal bed. J Hydraul Eng. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000099

    Article  Google Scholar 

  19. Cochard S, Ancey C (2008) Tracking the free surface of time-dependent flows: Image processing for the dam-break problem. Exp Fluids. https://doi.org/10.1007/s00348-007-0374-3

    Article  MATH  Google Scholar 

  20. Spinewine B, Zech Y (2007) Small-scale laboratory dam-break waves on movable beds. J Hydraul Res. https://doi.org/10.1080/00221686.2007.9521834

    Article  Google Scholar 

  21. Kocaman S, Ozmen-Cagatay H (2015) Investigation of dam-break induced shock waves impact on a vertical wall. J Hydrol. https://doi.org/10.1016/j.jhydrol.2015.03.040

    Article  Google Scholar 

  22. Crespo AJC, Gómez-Gesteira M, Dalrymple RA (2008) Modeling dam break behavior over a wet bed by a SPH technique. J Waterw Port Coast Ocean Eng. https://doi.org/10.1061/(ASCE)0733-950X(2008)134:6(313)

    Article  Google Scholar 

  23. Postacchini M, Othman IK, Brocchini M, Baldock TE (2014) Sediment transport and morphodynamics generated by a dam-break swash uprush: coupled vs uncoupled modeling. Coast Eng. https://doi.org/10.1016/j.coastaleng.2014.04.003

    Article  Google Scholar 

  24. Yang C, Lin B, Jiang C, Liu Y (2010) Predicting near-field dam-break flow and impact force using a 3D model. J Hydraul Res. https://doi.org/10.1080/00221686.2010.531099

    Article  Google Scholar 

  25. Biscarini C, Di Francesco S, Manciola P (2010) CFD modelling approach for dam break flow studies. Hydrol Earth Syst Sci. https://doi.org/10.5194/hess-14-705-2010

  26. Hu KC, Hsiao SC, Hwung HH, Wu TR (2012) Three-dimensional numerical modeling of the interaction of dam-break waves and porous media. Adv Water Resour. https://doi.org/10.1016/j.advwatres.2012.06.007

    Article  Google Scholar 

  27. LaRocque LA, Imran J, Chaudhry MH (2013) Experimental and numerical investigations of two-dimensional dam-break flows. J Hydraul Eng. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000705

    Article  Google Scholar 

  28. Ozmen-Cagatay H, Kocaman S (2010) Dam-break flows during initial stage using SWE and RANS approaches. J Hydraul Res. https://doi.org/10.1080/00221686.2010.507342

    Article  Google Scholar 

  29. Mingham CG, Causon DM (1998) High-resolution finite-volume method for shallow water flows. J Hydraul Eng. https://doi.org/10.1061/(ASCE)0733-9429(1998)124:6(605)

    Article  Google Scholar 

  30. Fondelli T, Andreini A, Facchini B (2015) Numerical simulation of dam-break problem using an adaptive meshing approach. Energy Procedia. https://doi.org/10.1016/j.egypro.2015.12.038

    Article  Google Scholar 

  31. Elsafi SH (2014) Artificial neural networks (ANNs) for flood forecasting at Dongola Station in the River Nile, Sudan. Alexandria Eng J. https://doi.org/10.1016/j.aej.2014.06.010

    Article  Google Scholar 

  32. Feng LH, Lu J (2010) The practical research on flood forecasting based on artificial neural networks. Expert Syst Appl. https://doi.org/10.1016/j.eswa.2009.09.037

    Article  Google Scholar 

  33. Liu Z, Merwade V (2019) Separation and prioritization of uncertainty sources in a raster based flood inundation model using hierarchical Bayesian model averaging. J Hydrol. https://doi.org/10.1016/j.jhydrol.2019.124100

    Article  Google Scholar 

  34. Aziz K, Rahman A, Fang G, Haddad K, Shrestha S (2010) Design flood estimation for ungauged catchments: application of artificial neural networks for eastern Australia. In: World environment water resource congress 2010 challenges change—proceedings of the world environment water resource congress 2010. https://doi.org/10.1061/41114(371)293

  35. Kişi Ö (2008) River flow forecasting and estimation using different artificial neural network techniques. Hydrol Res 39:27–40. https://doi.org/10.2166/nh.2008.026

    Article  Google Scholar 

  36. Sun S, Yan H, Lipeme Kouyi G (2014) Artificial neural network modelling in simulation of complex flow at open channel junctions based on large data sets. Environ Model Softw. https://doi.org/10.1016/j.envsoft.2014.08.026

    Article  Google Scholar 

  37. Kişi Ö (2004) River flow modeling using artificial neural networks. J Hydrol Eng 9:21. https://doi.org/10.1061/(ASCE)1084-0699(2004)9:1(60)

    Article  Google Scholar 

  38. Malekmohamadi I, Bazargan-Lari MR, Kerachian R, Nikoo MR, Fallahnia M (2011) Evaluating the efficacy of SVMs, BNs, ANNs and ANFIS in wave height prediction. Ocean Eng. https://doi.org/10.1016/j.oceaneng.2010.11.020

    Article  Google Scholar 

  39. Makarynskyy O (2004) Improving wave predictions with artificial neural networks. Ocean Eng 31:709–724. https://doi.org/10.1016/j.oceaneng.2003.05.003

    Article  Google Scholar 

  40. Chinh LV, Hiramatsu K, Harada M, Mori M (2009) Estimation of water levels in a main drainage canal in a flat low-lying agricultural area using artificial neural network models. Agric Water Manag. https://doi.org/10.1016/j.agwat.2009.04.005

    Article  Google Scholar 

  41. Liu Z, Merwade V (2018) Accounting for model structure, parameter and input forcing uncertainty in flood inundation modeling using Bayesian model averaging. J Hydrol. https://doi.org/10.1016/j.jhydrol.2018.08.009

    Article  Google Scholar 

  42. Jahangir MH, Mousavi Reineh SM, Abolghasemi M (2019) Spatial predication of flood zonation mapping in Kan River Basin, Iran, using artificial neural network algorithm. Weather Clim Extrem. https://doi.org/10.1016/j.wace.2019.100215

    Article  Google Scholar 

  43. Emiroglu ME, Bilhan O, Kisi O (2011) Neural networks for estimation of discharge capacity of triangular labyrinth side-weir located on a straight channel. Expert Syst Appl. https://doi.org/10.1016/j.eswa.2010.07.058

    Article  MATH  Google Scholar 

  44. Sahu M, Khatua KK, Mahapatra SS (2011) A neural network approach for prediction of discharge in straight compound open channel flow. Flow Meas Instrum 22:34. https://doi.org/10.1016/j.flowmeasinst.2011.06.009

    Article  Google Scholar 

  45. Romano M, Liong SY, Vu MT, Zemskyy P, Doan CD, Dao MH, Tkalich P (2009) Artificial neural network for tsunami forecasting. J Asian Earth Sci. https://doi.org/10.1016/j.jseaes.2008.11.003

    Article  Google Scholar 

  46. Rings J, Vrugt JA, Schoups G, Huisman JA, Vereecken H (2012) Bayesian model averaging using particle filtering and Gaussian mixture modeling: theory, concepts, and simulation experiments. Water Resour Res. https://doi.org/10.1029/2011WR011607

    Article  Google Scholar 

  47. Sadegh M, Vrugt JA (2014) Approximate Bayesian computation using markov chain Monte Carlo simulation: DREAM (ABC). Water Resour Res. https://doi.org/10.1002/2014WR015386

    Article  Google Scholar 

  48. Vrugt JA, Robinson BA (2007) Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian model averaging. Water Resour Res. https://doi.org/10.1029/2005WR004838

    Article  Google Scholar 

  49. Vosoughi F, Nikoo MR, Rakhshandehroo G, Adamowski JF, Alamdari N, Gandomi AH, Al-Wardy M (2021) Experimental videos in scrutinizing multiphase shock flood wave over different downstream initial conditions. Mendeley Data. https://doi.org/10.17632/bxx79583b6.2

    Article  Google Scholar 

  50. Vosoughi F, Nikoo MR, Rakhshandehroo G, Adamowski JF, Alamdari N, Gandomi AH, Al-Wardy M (2021) Experimental dataset on water levels in the study of flash flood wave without sediment (clear water) over bumpy downstream. Mendeley Data. https://doi.org/10.17632/64sy6w5vkz.3

    Article  Google Scholar 

  51. Vosoughi F, Nikoo MR, Rakhshandehroo G, Adamowski JF, Alamdari N, Gandomi AH, Al-Wardy M (2021) Experimental dataset on water levels in the study of multi-layer shock flood wave over bumpy downstream. Mendeley Data. https://doi.org/10.17632/sj4sthhryn.3

    Article  Google Scholar 

  52. Vosoughi F, Nikoo MR, Rakhshandehroo G, Adamowski JF, Alamdari N, Gandomi AH, Al-Wardy M (2021) Experimental dataset on sediment depths in the study of multi-layer shock flood wave over bumpy downstream bed. Mendeley Data. https://doi.org/10.17632/mmp3dhv9fj.3

    Article  Google Scholar 

  53. Vosoughi F, Nikoo MR, Rakhshandehroo G, Adamowski JF, Gandomi AH (2022) Downstream semi-circular obstacles' influence on floods arising from the failure of dams with different levels of reservoir silting. Phys Fluids. 34:013312. https://doi.org/10.1063/5.0079791

    Article  Google Scholar 

  54. Vosoughi F, Nikoo MR, Rakhshandehroo G, Sadegh M (2020) Experimental study and numerical verification of silted-up dam break. J Hydrol. 590:125267.  https://doi.org/10.1016/j.jhydrol.2020.125267

    Article  Google Scholar 

  55. Vosoughi F, Nikoo MR, Rakhshandehroo G, Gandomi AH (2021) Experimental dataset on water levels sediment depths and wave front celerity values in the study of multiphase shock wave for different initial up- and down-stream conditions. Data Br. 36:107082. https://doi.org/10.1016/j.dib.2021.107082

    Article  Google Scholar 

  56. Brentan BM, Luvizotto E, Herrera M, Izquierdo J, Pérez-García R (2017) Hybrid regression model for near real-time urban water demand forecasting. J Comput Appl Math 309:532–541. https://doi.org/10.1016/j.cam.2016.02.009

    Article  MathSciNet  MATH  Google Scholar 

  57. Shieh G (2008) Improved shrinkage estimation of squared multiple correlation coefficient and squared cross-validity coefficient. Organ Res Methods. https://doi.org/10.1177/1094428106292901

    Article  Google Scholar 

  58. Ma Y, Hong Y, Chen Y, Yang Y, Tang G, Yao Y, Long D, Li C, Han Z, Liu R (2018) Performance of optimally merged multisatellite precipitation products using the dynamic bayesian model averaging scheme over the tibetan plateau. J Geophys Res Atmos. https://doi.org/10.1002/2017JD026648

    Article  Google Scholar 

  59. Raftery AE, Gneiting T, Balabdaoui F, Polakowski M (2005) Using Bayesian model averaging to calibrate forecast ensembles. Mon Weather Rev. https://doi.org/10.1175/MWR2906.1

    Article  Google Scholar 

  60. Vrugt JA (2017) MODELAVG: A MATLAB toolbox for post processing of model ensembles

  61. Zhu G, Li X, Zhang K, Ding Z, Han T, Ma J, Huang C, He J, Ma T (2016) Multi-model ensemble prediction of terrestrial evapotranspiration across north China using Bayesian model averaging. Hydrol Process. https://doi.org/10.1002/hyp.10832

    Article  Google Scholar 

  62. Vrugt JA, ter Braak CJF, Clark MP, Hyman JM, Robinson BA (2008) Treatment of input uncertainty in hydrologic modeling: doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour Res. https://doi.org/10.1029/2007wr006720

    Article  Google Scholar 

  63. Vrugt JA, Ter Braak CJF, Diks CGH, Robinson BA, Hyman JM, Higdon D (2009) Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int J Nonlinear Sci Numer Simul. https://doi.org/10.1515/IJNSNS.2009.10.3.273

    Article  Google Scholar 

  64. Vrugt JA (2016) Markov chain Monte Carlo simulation using the DREAM software package: theory, concepts, and MATLAB implementation. Environ Model Softw. https://doi.org/10.1016/j.envsoft.2015.08.013

    Article  Google Scholar 

  65. Vrugt JA, ter Braak CJF, Diks CGH, Schoups G (2013) Hydrologic data assimilation using particle Markov chain Monte Carlo simulation: theory, concepts and applications. Adv Water Resour. https://doi.org/10.1016/j.advwatres.2012.04.002

    Article  Google Scholar 

  66. Gelman A, Rubin DB (1992) Inference from iterative simulation using multiple sequences. Stat Sci. https://doi.org/10.1214/ss/1177011136

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors wish to express their gratitude to Mr Jasper Vrugt, due to the assistance provided by adopting “MODELAVG toolbox”. The authors are also immensely grateful to Prof. Jan Adamowski for his comments on an earlier version of the manuscript and for sharing his pearls of wisdom with us during the course of this research.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Civil and Environmental Engineering Department, Shiraz University, Shiraz, Iran

    Foad Vosoughi & Gholamreza Rakhshandehroo

  2. Department of Civil and Architectural Engineering, Sultan Qaboos University, Muscat, Oman

    Mohammad Reza Nikoo

  3. Civil and Environmental Engineering Department, Florida State University, Tallahassee, USA

    Nasrin Alamdari

  4. Faculty of Engineering and Information Technology, University of Technology Sydney, Ultimo, NSW, 2007, Australia

    Amir H. Gandomi

  5. Department of Soils, Water and Agricultural Engineering, Sultan Qaboos University, SQU, Muscat, Oman

    Malik Al-Wardy

Authors
  1. Foad Vosoughi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mohammad Reza Nikoo
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Gholamreza Rakhshandehroo
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Nasrin Alamdari
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Amir H. Gandomi
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Malik Al-Wardy
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

FV Conceptualization, Software, Validation, Investigation, Resources, Data Curation, Writing—Original Draft, Visualization, Writing—Review and Editing, MRN Conceptualization, Methodology, Supervision, Reviewing—Original Draft, Validation, Resources, Visualization, Writing—Review and Editing, GR Conceptualization, Methodology, Supervision, Writing—Review and Editing, NA Supervision, Writing—Review and Editing, AHG Supervision, Writing—Review and Editing, MA-W Supervision, Writing—Review and Editing.

Corresponding author

Correspondence to Mohammad Reza Nikoo.

Ethics declarations

Conflict of interest

The authors declared that there is no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (PDF 1889 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vosoughi, F., Nikoo, M.R., Rakhshandehroo, G. et al. The application of Bayesian model averaging based on artificial intelligent models in estimating multiphase shock flood waves. Neural Comput & Applic 34, 20411–20429 (2022). https://doi.org/10.1007/s00521-022-07528-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07528-3

Keywords