Skip to main content
SpringerLink
Log in

Self-expressiveness property-induced structured optimal graph for unsupervised feature selection

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

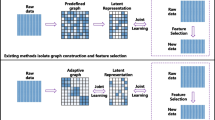
Feature selection is an important step for high-dimensional data clustering, reducing the redundancy of the raw feature set. In this paper, we focus on graph-based embedded feature selection and introduce a self-expressiveness property induced structured optimal graph feature selection (SPSOG-FS) algorithm. The proposed model incorporates both the advantages of data self-expressive property and the structured optimal graph (SOG) model. Specifically, in SPSOG-FS, a simple yet effective self-expressiveness constraint is proposed to thoroughly investigate the relations between local features. Simultaneously, we apply the SOG model to keep the original data’s local structure in low-dimensional space. As a result, both feature interaction and the local structural similarity of samples are taken into consideration. In addition, we also propose an efficient method named “density peaks-based automatic clustering” (DPBAC) to estimate the number of clusters, which is a necessary prior in graph-based FS but usually unknown in real-world scenarios. According to experimental results on benchmark datasets, our proposed FS approach outperforms numerous state-of-the-art methods. Additionally, the experiments demonstrate DPBAC’s capability for determining the number of clusters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data availability

The datasets generated during and/or analyzed during the current study are available in the UCI repository, http://archive.ics.uci.edu/ml/.

References

  1. AlSukker A, Khushaba RN, Al-Ani A (2010) Enhancing the diversity of genetic algorithm for improved feature selection. In: 2010 IEEE international conference on systems, man and cybernetics, IEEE, pp 1325–1331

  2. Belhumeur PN, Hespanha JP, Kriegman DJ (1997) Eigenfaces vs. fisherfaces: recognition using class specific linear projection. IEEE Trans Pattern Anal Mach Intell 19(7):711–720

    Article  Google Scholar 

  3. Belkin M, Niyogi P (2001) Laplacian eigenmaps and spectral techniques for embedding and clustering. In: Nips, pp 585–591

  4. Cai D, Zhang C, He X (2010) Unsupervised feature selection for multi-cluster data. In: Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining, pp 333–342

  5. Chandrashekar G, Sahin F (2014) A survey on feature selection methods. Comput Electr Eng 40(1):16–28

    Article  Google Scholar 

  6. Cole R, Fanty M (1990) Spoken letter recognition. In: Speech and natural language: proceedings of a workshop held at Hidden Valley, Pennsylvania, pp 24–27

  7. Ding D, Yang X, Xia F et al (2020) Unsupervised feature selection via adaptive hypergraph regularized latent representation learning. Neurocomputing 378:79–97

    Article  Google Scholar 

  8. Ding J, He X, Yuan J et al (2018) Automatic clustering based on density peak detection using generalized extreme value distribution. Soft Comput 22(9):2777–2796

    Article  Google Scholar 

  9. Elhamifar E, Vidal R (2013) Sparse subspace clustering: algorithm, theory, and applications. IEEE Trans Pattern Anal Mach Intell 35(11):2765–2781

    Article  Google Scholar 

  10. Ester M, Kriegel HP, Sander J et al (1996) A density-based algorithm for discovering clusters in large spatial databases with noise. In: kdd, pp 226–231

  11. Fan K (1949) On a theorem of Weyl concerning eigenvalues of linear transformations i. Proc Natl Acad Sci USA 35(11):652

    Article  MathSciNet  Google Scholar 

  12. Guyon I, Elisseeff A (2003) An introduction to variable and feature selection. J Mach Learn Res 3:1157–1182

    MATH  Google Scholar 

  13. Hall MA (2000) Correlation-based feature selection of discrete and numeric class machine learning

  14. Hancer E, Xue B, Zhang M (2018) Differential evolution for filter feature selection based on information theory and feature ranking. Knowl Based Syst 140:103–119

    Article  Google Scholar 

  15. Hou C, Nie F, Li X et al (2013) Joint embedding learning and sparse regression: a framework for unsupervised feature selection. IEEE Trans Cybern 44(6):793–804

    Google Scholar 

  16. Hull JJ (1994) A database for handwritten text recognition research. IEEE Trans Pattern Anal Mach Intell 16(5):550–554

    Article  Google Scholar 

  17. Khan J, Wei JS, Ringner M et al (2001) Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat Med 7(6):673–679

    Article  Google Scholar 

  18. Lee M, Lee J, Lee H et al (2015) Membership representation for detecting block-diagonal structure in low-rank or sparse subspace clustering. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 1648–1656

  19. Li X, Zhang H, Zhang R et al (2018) Generalized uncorrelated regression with adaptive graph for unsupervised feature selection. IEEE Trans Neural Netw Learn Syst 30(5):1587–1595

    Article  MathSciNet  Google Scholar 

  20. Li Y, Li T, Liu H (2017) Recent advances in feature selection and its applications. Knowl Inf Syst 53(3):551–577

    Article  Google Scholar 

  21. Longford NT (1987) A fast scoring algorithm for maximum likelihood estimation in unbalanced mixed models with nested random effects. Biometrika 74(4):817–827

    Article  MathSciNet  MATH  Google Scholar 

  22. Lyons MJ, Budynek J, Akamatsu S (1999) Automatic classification of single facial images. IEEE Trans Pattern Anal Mach Intell 21(12):1357–1362

    Article  Google Scholar 

  23. Ma Z, Yang Y, Nie F et al (2011) Exploiting the entire feature space with sparsity for automatic image annotation. In: Proceedings of the 19th ACM international conference on multimedia, pp 283–292

  24. Ma Z, Nie F, Yang Y et al (2012) Discriminating joint feature analysis for multimedia data understanding. IEEE Trans Multimedia 14(6):1662–1672

    Article  Google Scholar 

  25. Miao J, Niu L (2016) A survey on feature selection. Procedia Comput Sci 91:919–926

    Article  Google Scholar 

  26. Moradi P, Gholampour M (2016) A hybrid particle swarm optimization for feature subset selection by integrating a novel local search strategy. Appl Soft Comput 43:117–130

    Article  Google Scholar 

  27. Nene S, Nayar S, Murase H et al (1996) Columbia object image library (coil-20)

  28. Nie F, Huang H, Cai X et al (2010) Efficient and robust feature selection via joint \({{\ell }_{2,1}}\)-norms minimization. Adv Neural Inf Process Syst 23

  29. Nie F, Wang X, Huang H (2014) Clustering and projected clustering with adaptive neighbors. In: Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, pp 977–986

  30. Nie F, Zhu W, Li X (2016) Unsupervised feature selection with structured graph optimization. In: Proceedings of the AAAI conference on artificial intelligence

  31. Pearson KX (1900) On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond Edinb Dublin Philos Mag J Sci 50(302):157–175

    Article  MATH  Google Scholar 

  32. Peng X, Tang H, Zhang L et al (2015) A unified framework for representation-based subspace clustering of out-of-sample and large-scale data. IEEE Trans Neural Netw Learn Syst 27(12):2499–2512

    Article  MathSciNet  Google Scholar 

  33. Ray S, Turi RH (1999) Determination of number of clusters in k-means clustering and application in colour image segmentation. In: Proceedings of the 4th international conference on advances in pattern recognition and digital techniques, Citeseer, pp 137–143

  34. Ren P, Xiao Y, Chang X et al (2020) Structured optimal graph-based clustering with flexible embedding. IEEE Trans Neural Netw Learn Syst 31(10):3801–3813

    Article  MathSciNet  Google Scholar 

  35. Rodriguez A, Laio A (2014) Clustering by fast search and find of density peaks. Science 344(6191):1492–1496

    Article  Google Scholar 

  36. Sanguinetti G, Laidler J, Lawrence ND (2005) Automatic determination of the number of clusters using spectral algorithms. In: 2005 IEEE workshop on machine learning for signal processing, IEEE, pp 55–60

  37. Shi C, Ruan Q, An G (2014) Sparse feature selection based on graph Laplacian for web image annotation. Image Vis Comput 32(3):189–201

    Article  Google Scholar 

  38. Shi L, Du L, Shen YD (2014b) Robust spectral learning for unsupervised feature selection. In: 2014 IEEE international conference on data mining, IEEE, pp 977–982

  39. Tabakhi S, Moradi P, Akhlaghian F (2014) An unsupervised feature selection algorithm based on ant colony optimization. Eng Appl Artif Intell 32:112–123

    Article  Google Scholar 

  40. Wang F, Zhu L, Li J et al (2021) Unsupervised soft-label feature selection. Knowl Based Syst 219(106):847

    Google Scholar 

  41. Wang W, Yan Y, Nie F et al (2018) Flexible manifold learning with optimal graph for image and video representation. IEEE Trans Image Process 27(6):2664–2675

    Article  MathSciNet  MATH  Google Scholar 

  42. Yang Y, Shen HT, Ma Z, et al (2011) \({{\ell }_{2,1}}\)-norm regularized discriminative feature selection for unsupervised learning. In: IJCAI international joint conference on artificial intelligence

  43. Yaohui L, Zhengming M, Fang Y (2017) Adaptive density peak clustering based on k-nearest neighbors with aggregating strategy. Knowl Based Syst 133:208–220

    Article  Google Scholar 

  44. Yu L, Liu H (2003) Feature selection for high-dimensional data: a fast correlation-based filter solution. In: Proceedings of the 20th international conference on machine learning (ICML-03), pp 856–863

  45. Zeng H, Ym C (2010) Feature selection and kernel learning for local learning-based clustering. IEEE Trans Pattern Anal Mach Intell 33(8):1532–1547

    Article  Google Scholar 

  46. Zhao H, Li Q, Wang Z et al (2022) Joint adaptive graph learning and discriminative analysis for unsupervised feature selection. Cogn Comput 14(3):1211–1221

    Article  Google Scholar 

  47. Zhu J, Jang-Jaccard J, Liu T et al (2021) Joint spectral clustering based on optimal graph and feature selection. Neural Process Lett 53(1):257–273

    Article  Google Scholar 

  48. Zhu X, Zhang S, Hu R et al (2017) Local and global structure preservation for robust unsupervised spectral feature selection. IEEE Trans Knowl Data Eng 30(3):517–529

    Article  Google Scholar 

  49. Zhu X, Zhang S, Zhu Y et al (2022) Unsupervised spectral feature selection with dynamic hyper-graph learning. IEEE Trans Knowl Data Eng 34(6):3016–3028

    Google Scholar 

Download references

Acknowledgements

This work was supported in part by the Natural Science Foundation of China under Grants 61702336 and 71701132 and in part by Shenzhen Fundamental Research Program uder Grant JCYJ20200109110410133.

Author information

Authors and Affiliations

  1. College of Management, Shenzhen University, Shenzhen, 518055, China

    Hainan Guo & Haowen Xia

  2. College of Computer Science and Software Engineering, Shenzhen University, Shenzhen, 518061, China

    Yu Zhou

Authors
  1. Hainan Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Haowen Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu Zhou.

Ethics declarations

Conflict of interest

The authors have no competing interests to declare that are relevant to the content of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guo, H., Xia, H. & Zhou, Y. Self-expressiveness property-induced structured optimal graph for unsupervised feature selection. Neural Comput & Applic 34, 22583–22599 (2022). https://doi.org/10.1007/s00521-022-07678-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07678-4

Keywords

Search

Navigation