Skip to main content

Advertisement

Springer Nature Link
Log in

New Pythagorean fuzzy-based distance operators and their applications in pattern classification and disease diagnostic analysis

  • S.I.: Interpretation of Deep Learning
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

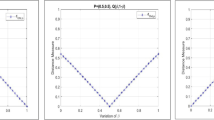
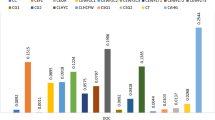
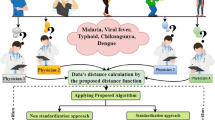
Pythagorean fuzzy set is a notion that takes a broader view at intuitionistic fuzzy set with a higher prospect of applications since it has a wider scope compared to IFS. On the other hand, distance measure is an efficient information measure for decision-making via deep learning approach, and thus, this paper proposes a new tri-parametric distance and its weighted version under Pythagorean fuzzy environment with improved performance indexes compared to the hitherto tri-parametric distance measures in the literature. The proposed Pythagorean fuzzy-based distance operators are new approaches because they take into account the three conventional number of parameters of PFSs against the existing practice, and as well incorporate the whole parameters to avoid error due to exclusion as witnessed in other distance operators. Some theorems are presented to validate the new Pythagorean fuzzy distance techniques with regards to its alignment with distance operator’s properties. We demonstrate the applications of the proposed Pythagorean fuzzy distance and its weighted version in cases involving pattern classification and disease diagnosis via deep learning approach where patterns, diseases and patients are presented as Pythagorean fuzzy values. Finally, some comparative analyses of the new tri-parametric Pythagorean fuzzy distance and its weighted version alongside some similar existing distances are presented in terms of the applications to showcase the superiority of the present Pythagorean fuzzy distance techniques.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

This paper has no associated data.

References

  1. Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353

    Article  MATH  Google Scholar 

  2. Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Set Syst 20:87–96

    Article  MATH  Google Scholar 

  3. Atanassov KT (1989) Geometrical interpretation of the elements of the intuitionistic fuzzy objects. Preprint IM-MFAIS-1-89, Sofia

  4. Yager RR (2013) Pythagorean membership grades in multicriteria decision making. Technical Report MII-3301 Machine Intelligence Institute, Iona College, New Rochelle, NY

  5. Yager RR, Abbasov AM (2013) Pythagorean membership grades, complex numbers and decision making. Int J Intell Syst 28(5):436–452

    Article  Google Scholar 

  6. Boran FE, Akay D (2014) A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition. Inf Sci 255(10):45–57

    Article  MATH  MathSciNet  Google Scholar 

  7. Chen SM, Chang CH (2015) A novel similarity measure between Atanassov’s intuitionistic fuzzy sets based on transformation techniques with applications to pattern recognition. Inf Sci 291:96–114

    Article  Google Scholar 

  8. Szmidt E, Kacprzyk J (2001) Intuitionistic fuzzy sets in some medical applications. Note IFS 7(4):58–64

    MATH  Google Scholar 

  9. Atanassov KT (1999) Intuitionistic fuzzy sets: theory and applications. Physica-Verlag, Heidelberg

    Book  MATH  Google Scholar 

  10. Wang W, Xin X (2005) Distance measure between intuitionistic fuzzy sets. Pattern Recog Lett 26:2063–2069

    Article  Google Scholar 

  11. Hatzimichailidis AG, Papakostas AG, Kaburlasos VG (2012) A novel distance measure of intuitionistic fuzzy sets and its application to pattern recognition problems. Int J Intell Syst 27:396–409

    Article  Google Scholar 

  12. Liu P, Chen SM (2017) Group decision making based on Heronian aggregation operators of intuitionistic fuzzy numbers. IEEE Trans Cybern 47(9):2514–2530

    Article  Google Scholar 

  13. Burillo P, Bustince H (1996) Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Set Syst 78:305–315

    Article  MATH  MathSciNet  Google Scholar 

  14. Szmidt E, Kacprzyk J (2000) Distances between intuitionistic fuzzy sets. Fuzzy Set Syst 114:505–518

    Article  MATH  MathSciNet  Google Scholar 

  15. Davvaz B, Sadrabadi EH (2016) An application of intuitionistic fuzzy sets in medicine. Int J Biomath 9(3):1650037

    Article  MATH  MathSciNet  Google Scholar 

  16. Du YQ, Hou F, Zafar W, Yu Q, Zhai Y (2017) A novel method for multiattribute decision making with interval-valued Pythagorean fuzzy linguistic information. Int J Intell Syst 32(10):1085–1112

    Article  Google Scholar 

  17. Garg H (2016) A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int J Intell Syst 31(9):886–920

    Article  Google Scholar 

  18. Garg H (2017) Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision making process. Int J Intell Syst 32(6):597–630

    Article  Google Scholar 

  19. Garg H (2018) Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision making process. Int J Intell Syst 33(6):1234–1263

    Article  Google Scholar 

  20. Liang D, Xu Z (2017) The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy fets. Appl Soft Comput 60:167–179

    Article  Google Scholar 

  21. Ejegwa PA, Wen S, Feng Y, Zhang W, Liu J (2022) A three-way Pythagorean fuzzy correlation coefficient approach and its applications in deciding some real-life problems. Appl Intell. https://doi.org/10.1007/s10489-022-03415-5

    Article  Google Scholar 

  22. Ejegwa PA, Wen S, Feng Y, Zhang W, Chen J (2021) Some new Pythagorean fuzzy correlation techniques via statistical viewpoint with applications to decision-making problems. J Intell Fuzzy Syst 40(5):9873–9886

    Article  Google Scholar 

  23. Ejegwa PA, Wen S, Feng Y, Zhang W (2021) Determination of pattern recognition problems based on a Pythagorean fuzzy correlation measure from statistical viewpoint. In: Proc 13th int conf advanced comput intell. Wanzhou, China, pp 132–139

  24. Zhang XL, Xu ZS (2014) Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 29:1061–1078

    Article  MathSciNet  Google Scholar 

  25. Ejegwa PA, Jana C, Pal M (2022) Medical diagnostic process based on modified composite relation on Pythagorean fuzzy multisets. Granul Comput 7:15–23

    Article  Google Scholar 

  26. Ejegwa PA, Onyeke IC (2022) Some new distance and similarity algorithms for Pythagorean fuzzy sets with application in decision-making problems. In: Broumi S (ed.), Handbook of research on advances and applications of fuzzy sets and logic, pp 192–211, Hershey, Pennsylvania 17033–1240, USA

  27. Peng X, Yuan H, Yang Y (2017) Pythagorean fuzzy information measures and their applications. Int J Intell Syst 32:991–1029

    Article  Google Scholar 

  28. Peng X (2019) New similarity measure and distance measure for Pythagorean fuzzy set. Complex Intell Syst 5(2):101–111

    Article  Google Scholar 

  29. Meng L, Wei X (2021) Research on evaluation of sustainable development of new urbanization from the perspective of urban agglomeration under the Pythagorean fuzzy sets. Discret Dyn Nat Soc. https://doi.org/10.1155/2021/2445025

    Article  MATH  Google Scholar 

  30. Wan Z, Shi M, Yang F, Zhu G (2021) A novel Pythagorean group decision-making method based on evidence theory and interactive power averaging operator. Complexity. https://doi.org/10.1155/2021/9964422

    Article  Google Scholar 

  31. Zulqarnain RM, Siddique I, Jarad F, Hamed YS, Abualnaja KM, Iampan A (2022) Einstein aggregation operators for Pythagorean fuzzy soft sets with their application in multiattribute group decision-making. J Funct Spaces. https://doi.org/10.1155/2022/1358675

    Article  MATH  MathSciNet  Google Scholar 

  32. Saeed M, Ahmad MR, Rahman AU (2022) Refined Pythagorean fuzzy sets: properties, set-theoretic operations and axiomatic results. J Comput Cogn Eng. https://doi.org/10.47852/bonviewJCCE2023512225

    Article  Google Scholar 

  33. Akram M, Zahid K, Alcantud JCR (2022) A new outranking method for multicriteria decision making with complex Pythagorean fuzzy information. Neural Comput Appl 34:8069–8102

    Article  Google Scholar 

  34. Ye J, Chen TY (2022) Pythagorean fuzzy sets combined with the PROMETHEE method for the selection of cotton woven fabric. J Nat Fibers. https://doi.org/10.1080/15440478.2022.2072993

    Article  Google Scholar 

  35. Li DQ, Zeng WY (2018) Distance measure of Pythagorean fuzzy sets. Int J Intell Syst 33:348–361

    Article  Google Scholar 

  36. Ejegwa PA (2020) Distance and similarity measures for Pythagorean fuzzy sets. Granul Comput 5(2):225–238

    Article  MathSciNet  Google Scholar 

  37. Diamond P, Kloeden P (1994) Metric spaces of fuzzy sets theory and applications. Word Scientific, Singapore

    Book  MATH  Google Scholar 

  38. Ejegwa PA (2020) Modified Zhang and Xu’s Distance measure of Pythagorean fuzzy sets and its application to pattern recognition problems. Neural Comput Appl 32(14):10199–10208

    Article  Google Scholar 

  39. Zeng W, Li D, Yin Q (2018) Distance and similarity measures of Pythagorean fuzzy sets and their applications to multiple criteria group decision making. Int J Intell Syst 33(11):2236–2254

    Article  Google Scholar 

  40. Ejegwa PA, Awolola JA (2021) Novel distance measures for Pythagorean fuzzy sets with applications to pattern recognition problems. Granul Comput 6:181–189

    Article  Google Scholar 

  41. Hussain Z, Yang MS (2019) Distance and similarity measures of Pythagorean fuzzy sets based on the Hausdorff metric with application to fuzzy TOPSIS. Int J Intell Syst 34(10):2633–2654

    Article  Google Scholar 

  42. Xiao F, Ding W (2019) Divergence measure of Pythagorean fuzzy sets and its application in medical diagnosis. Appl Soft Comput 79:254–267

    Article  Google Scholar 

  43. Mahanta J, Panda S (2021) Distance measure for Pythagorean fuzzy sets with varied applications. Neural Comput Appl 33:17161–17171

    Article  Google Scholar 

  44. Sarabu A, Santra AK (2021) Human action recognition in videos using convolution long short-term memory network with Spatio-temporal networks. Emerg Sci J 5(1):25–33

    Article  Google Scholar 

  45. Bagherzadeh SHZ, Toosizadeh S (2022) Eye tracking algorithm based on multi model Kalman filter. High Tech Innov J 3(1):15–27

    Google Scholar 

Download references

Funding

This work is supported by Foundation of Chongqing Municipal Key Laboratory of Institutions of Higher Education ([2017]3), Foundation of Chongqing Development and Reform Commission (2017[1007]), and Foundation of Chongqing Three Gorges University.

Author information

Authors and Affiliations

  1. Key Laboratory of Intelligent Information Processing and Control, Chongqing Three Gorges University, Wanzhou, Chongqing, 404100, China

    Paul Augustine Ejegwa, Yuming Feng & Johnson Mobolaji Agbetayo

  2. Department of Mathematics, University of Agriculture, P.M.B. 2373, Makurdi, Nigeria

    Paul Augustine Ejegwa

  3. Chongqing Engineering Research Center of Internet of Things and Intelligent Control Technology, Chongqing Three Gorges University, Wanzhou, Chongqing, 404100, China

    Shuyu Tang & Xiangguang Dai

Authors
  1. Paul Augustine Ejegwa
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yuming Feng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Shuyu Tang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Johnson Mobolaji Agbetayo
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Xiangguang Dai
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors contribute equally to this paper.

Corresponding author

Correspondence to Yuming Feng.

Ethics declarations

Conflict of interest

The authors declare that they have no competing interests.

Ethical approval

Non applicable.

Informed consent

Yes.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ejegwa, P.A., Feng, Y., Tang, S. et al. New Pythagorean fuzzy-based distance operators and their applications in pattern classification and disease diagnostic analysis. Neural Comput & Applic 35, 10083–10095 (2023). https://doi.org/10.1007/s00521-022-07679-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07679-3

Keywords