Skip to main content

Advertisement

Springer Nature Link
Log in

Multi-objective sparse echo state network

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

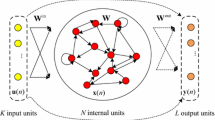
The echo state network (ESN) has been widely applied for nonlinear system modeling. However, the too large reservoir size of ESN will lead to overfitting problem and reduce generalization performance. To balance reservoir size and training performance, the multi-objective sparse echo state network (MOS-ESN) is proposed. Firstly, the ESN design problem is formulated as a two-objective optimization problem, which is solved by the decomposition-based multi-objective optimization algorithm (MOEA/D). Secondly, to accelerate algorithm convergence, the local search strategy is designed, which combines the l1 or l0 norm regularization and coordinate descent algorithm, respectively. Thirdly, to produce more solutions around the knee point, an adaptive weight vectors updating method is proposed, which is based on decision maker interest. Experimental results show that the MOS-ESN outperforms other methods in terms of network sparseness and prediction accuracy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. Zhu T, Luo L, Zhang XL et al (2017) Time-series approaches for forecasting the number of hospital daily discharged inpatients. IEEE J Biomed Health Inform 21(2):515–526

    Google Scholar 

  2. Zhang H, Cao X, John H, Tommy C (2017) Object-level video advertising: an optimization framework. IEEE Trans Industr Inf 13(2):520–531

    Google Scholar 

  3. Safari N, Chung CY, Price G (2018) A novel multi-step short-term wind power prediction framework based on chaotic time series analysis and singular spectrum analysis. IEEE Trans Power Syst 33(1):590–601

    Google Scholar 

  4. Lee R (2020) Chaotic type-2 transient-fuzzy deep neuro-oscillatory network (CT2TFDNN) for worldwide financial prediction. IEEE Trans Fuzzy Syst 28(4):731–745

    Google Scholar 

  5. Li JD, Tang H, Wu Z et al (2019) A stable autoregressive moving average hysteresis model in flexure fast tool servo control. IEEE Trans Autom Sci Eng 16(3):1484–1493

    Google Scholar 

  6. Zhou D, Al-Durra A, Zhang K et al (2019) A robust prognostic indicator for renewable energy technologies: a novel error correction grey prediction model. IEEE Trans Industr Electron 66(12):9312–9325

    Google Scholar 

  7. Ciprian C, Masychev K, Ravan M et al (2020) A machine learning approach using effective connectivity to predict response to clozapine treatment. IEEE Trans Neural Syst Rehabil Eng 28(12):2598–2607

    Google Scholar 

  8. Park YM, Moon UC, Lee KY (1996) A self-organizing power system stabilizer using fuzzy auto-regressive moving average (FARMA) model. IEEE Trans Energy Convers 11(2):442–448

    Google Scholar 

  9. Xie N, Liu S (2015) Interval grey number sequence prediction by using non-homogenous exponential discrete grey forecasting model. J Syst Eng Electron 26(1):96–102

    Google Scholar 

  10. Zhang K, Liu Z, Zheng L (2020) Short-term prediction of passenger demand in multi-zone level: temporal convolutional neural network with multi-task learning. IEEE Trans Intell Transp Syst 21(4):1480–1490

    Google Scholar 

  11. Kuang W, Chan YL, Tsang SH et al (2019) Machine learning-based fast intra mode decision for HEVC screen content coding via decision trees. IEEE Trans Circuits Syst Video Technol 30(5):1481–1496

    Google Scholar 

  12. Han SJ, Bae KY, Park HS et al (2016) Solar power prediction based on satellite images and support vector machine. IEEE Transactions on Sustainable Energy 7(3):1255–1263

    Google Scholar 

  13. Liu YT, Lin YY, Wu SL et al (2015) Brain dynamics in predicting driving fatigue using a recurrent self-evolving fuzzy neural network. IEEE Transactions on Neural Networks and Learning Systems 27(2):1–14

    Google Scholar 

  14. Zhang HJ, Li JX, Ji YZ, Yue H (2017) Subtitle understanding by character-level sequence-to-sequence learning. IEEE Trans Industr Inf 13(2):616–624

    Google Scholar 

  15. Zsuzsa P, Radu EP, Jozsef KT et al (2006) Use of multi-parametric quadratic programming in fuzzy control systems. Acta Polytechnica Hungarica 3(3):29–43

    Google Scholar 

  16. Rizvi SA, Wang LC (1997) Nonlinear vector prediction using feed-forward neural networks. IEEE Trans Image Process 6(10):1431–1436

    Google Scholar 

  17. Shi Z, Liang H, Dinavahi V (2017) Direct interval forecast of uncertain wind power based on recurrent neural networks. IEEE Transactions on Sustainable Energy 9(3):1177–1187

    Google Scholar 

  18. Jaeger H, Hass H (2004) Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 304:78–80

    Google Scholar 

  19. Wu Z, Li Q, Zhang HJ (2022) Chain-structure echo state network with stochastic optimization: methodology and application. IEEE Trans Neural Netw Learn Syst 33(5):1974–1985

    Google Scholar 

  20. Wu Z, Li Q, Xia XH (2021) Multi-timescale forecast of solar irradiance based on multi-task learning and echo state network approaches. IEEE Trans Industr Inf 17(1):300–310

    Google Scholar 

  21. Mantas L, Jaeger H (2009) Reservoir computing approaches to recurrent neural network training. Computer science review 3:127–149

    MATH  Google Scholar 

  22. Jaeger H (2007) Discovering multiscale dynamical features with hierarchical echo state networks. Jacobs University Bremen, Bremen

    Google Scholar 

  23. Jaeger H, Lukosevicius M, Popovici D et al (2007) Optimization and applications of echo state networks with leaky integrator neurons. Neural Netw 20(2007):335–352

    MATH  Google Scholar 

  24. Qiao J, Li F, Han H et al (2017) Growing echo-state network with multiple subreservoirs. IEEE Trans Neural Netw Learn Syst 28(2):391–404

    Google Scholar 

  25. Wang HS, Ni CJ, Yan XF (2017) Optimizing the echo state network based on mutual information for modeling fed-batch bioprocesses. Neurocomputing 225:111–118

    Google Scholar 

  26. Xu M, Han M (2017) Adaptive elastic echo state network for multivariate time series prediction. IEEE Trans Cybern 46(10):2173–2183

    Google Scholar 

  27. Yang C, Nie K, Qiao J et al (2022) Robust echo state network with sparse online learning. Inf Sci 594:95–117

    Google Scholar 

  28. Luo X, Chang X, Ban X (2016) Regression and classification using extreme learning machine based on l1-norm and l2-norm. Neurocomputing 174:179–186

    Google Scholar 

  29. Yang CL, Qiao JF, Wang L et al (2019) Dynamical regularized echo state network for time series prediction. Neural Comput Appl 31(10):6781–6794

    Google Scholar 

  30. Han M, Ren W, Xu M (2014) An improved echo state network via l1-norm regularization. Acta Automatica Sinica 40(11):2428–2435

    MATH  Google Scholar 

  31. Dzati A, Ramli, et al (2017) Fast kernel sparse representation classifier using improved smoothed-l0 norm. Proc Comput Sci 112:494–503

    Google Scholar 

  32. Yang CL, Qiao JF, Ahmad Z et al (2019) Online sequential echo state network with sparse RLS algorithm for time series prediction. Neural Netw 118:32–42

    MATH  Google Scholar 

  33. Qiao JF, Wang L, Yang CL (2018) Adaptive lasso echo state network based on modified Bayesian information criterion for nonlinear system modeling. Neural Comput Appl 31(10):6163–6177

    Google Scholar 

  34. Huang HZ, Gu YK, Du X (2006) An interactive fuzzy multi-objective optimization method for engineering design. Eng Appl Artif Intell 19(5):451–460

    Google Scholar 

  35. Zhang HJ, Sun YF, Zhao MB et al (2020) Bridging user interest to item content for recommender systems: an optimization model. IEEE Transactions on Cybern 50(10):4268–4280

    Google Scholar 

  36. Lin L, Yao X, Stolkin R et al (2014) An evolutionary multiobjective approach to sparse reconstruction. IEEE Trans Evol Comput 18(6):827–845

    Google Scholar 

  37. Rachmawati L, Srinivasan D (2009) Multiobjective evolutionary algorithm with controllable focus on the knees of the pareto front. IEEE Trans Evol Comput 13(4):810–824

    Google Scholar 

  38. Branke J, Deb K, Dierolf H et al (2004) Finding knees in multiobjective optimization. In: International Conference on Parallel Problem Solving from Nature, LNCS 3242:722–731

  39. Das I (1999) On characterizing the ‘knee’ of the pareto curve based on normal-boundary intersection. Struct Multidiscip Optimiz 18(2):107–115

    Google Scholar 

  40. Zhang Q (2007) MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Transa Evolut Comput 11(6):712–731

    Google Scholar 

  41. Deb K, Gupta S (2011) Understanding knee points in bicriteria problems and their implications as preferred solution principles. Eng Optim 43(11):1175–1204

    MathSciNet  Google Scholar 

  42. Weitian C, Brian DOA (2012) A combined multiple model adaptive control scheme and its application to nonlinear systems with nonlinear parameterization. IEEE Trans Autom Control 57(7):1778–1782

    MathSciNet  MATH  Google Scholar 

  43. Yang CL, Wu ZH, Qiao JF (2020) Design of echo state network with coordinate descent method and l1 regularization. Commun Comput Inf Sci 1265:357–367

    Google Scholar 

  44. Dong ZM, Wang XP, Tang LX (2020) MOEA/D with a self-adaptive weight vector adjustment strategy based on chain segmentation. Inf Sci 521:209–230

    MathSciNet  MATH  Google Scholar 

  45. Ishibuchi H, Yoshida T, Murata T (2003) Balance between genetic search and local search in memetic algorithms for multiobjective permutation flowshop scheduling. IEEE Trans Evol Comput 7(2):20

    Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China (61973010, 61890930–5,62021003, 61533002), in part by the National Natural Science Foundation of Beijing (4202006), and in part by the National Key Research and Development Project (2021ZD0112302, 2019YFC1906002, 2018YFC1900802

Author information

Authors and Affiliations

  1. Beijing Key Laboratory of Computational Intelligence and Intelligence System, Beijing Laboratory for Intelligent Environmental Protection, Faculty of Information Technology, Beijing Institute of Artificial Intelligence, Beijing University of Technology, Pingleyuan, Beijing, Beijing, 100124, China

    Cuili Yang & Zhanhong Wu

Authors
  1. Cuili Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhanhong Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Cuili Yang.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The parameters setting of different algorithms is given:

  • OESN: The reservoir has 1000 nodes. The reservoir sparsity s1 is chosen from the set (0.01, 0.015, …, 0.6), and the spectral radius of reservoir s2 is chosen from the set (0.1, 0.15, …, 0.95).

  • OESN-l1: The reservoir has same parameters as OESN. The regularization parameter λ1 is selected by (LASSO) method [33].

  • OESN-l0: The reservoir has same parameters as OESN. The regularization parameter λ0 is adaptively calculated [32].

  • CD-ESN-l1: The reservoir has same parameters as OESN. The regularization parameter λ is chosen from the set (0.05, 0.10, 0.15, …, 0.9) as suggested in [43].

  • CD-ESN-l0: The reservoir has same parameters as OESN. The regularization parameter λ is chosen from the set (0, 0.05, 0.15, …, 0.95).

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, C., Wu, Z. Multi-objective sparse echo state network. Neural Comput & Applic 35, 2867–2882 (2023). https://doi.org/10.1007/s00521-022-07711-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07711-6

Keywords