Skip to main content

Advertisement

Springer Nature Link
Log in

A novel fractional operator application for neural networks using proportional Caputo derivative

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

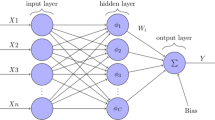
In machine learning models, one of the most popular models is artificial neural networks. The activation function is one of the important parameters of neural networks. In this paper, the sigmoid function is used as an activation function with a fractional derivative approach to minimize the convergence error in backpropagation and to maximize the generalization performance of neural networks. The proportional Caputo definition is considered a fractional derivative. We evaluated three neural network models on the usage of the proportional Caputo derivative. The results show that the proportional Caputo derivative approach has higher classification accuracy than traditional derivative models in backpropagation for neural networks with and without L2 regularization.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Data and material availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Code availability

The code and the weights for NN models will be shared on github with the acceptance at https://github.com/galtan-PhD/ProportionalCaputoNN.

References

  1. Wang J, Wen Y, Gou Y, Ye Z, Chen H (2017) Fractional-order gradient descent learning of BP neural networks with Caputo derivative. Neural Netw 89:19–30. https://doi.org/10.1016/j.neunet.2017.02.007

    Article  MATH  Google Scholar 

  2. Wang H, Yu Y, Wen G, Zhang S, Yu J (2015) Global stability analysis of fractional-order Hopfield neural networks with time delay. Neurocomputing 154:15–23. https://doi.org/10.1016/j.neucom.2014.12.031

    Article  Google Scholar 

  3. Bao C, Pu Y, Zhang Y (2018) Fractional-order deep backpropagation neural network. Comput Intell Neurosci 2018:1–10. https://doi.org/10.1155/2018/7361628

    Article  Google Scholar 

  4. Marchaud MA (1925) Sur les dérivées et sur les différences des fonctions de variables réelles. J Math Pures Appl 9:337–425

    MATH  Google Scholar 

  5. Caputo M (1967) Linear models of dissipation whose q is almost frequency independent-ii. Geophys J Int 13(5):529–539

    Article  Google Scholar 

  6. Liouville J (1832) Mémoire sur quelques quéstions de géometrie et de mécanique. J l’école Polytech 13(21):1–69

    Google Scholar 

  7. Hilfer R (2000). Applications of fractional calculus in physics. https://doi.org/10.1142/3779

  8. Meerschaert MM, Sikorskii A (2011) Stochastic Models for Fractional Calculus. De Gruyter, Berlin. https://doi.org/10.1515/9783110258165

  9. Caputo M, Fabrizio M (2015) A new definition of fractional derivative without singular kernel. Prog Fract Differ Appl 1(2):73–85. https://doi.org/10.12785/pfda/010201

    Article  Google Scholar 

  10. Atangana A, Baleanu D (2016) New fractional derivatives with nonlocal and non-singular kernel:theory and application to heat transfer model. Therm Sci 20(2):763–769. https://doi.org/10.2298/TSCI160111018AarXiv:1602.03408

    Article  Google Scholar 

  11. Baleanu D, Fernandez A, Akgül A (2020) On a fractional operator combining proportional and classical differintegrals. Mathematics 8(3):360. https://doi.org/10.3390/math8030360

    Article  Google Scholar 

  12. Viera-Martin E, Gómez-Aguilar JF, Solís-Pérez JE, Hernández-Pérez JA, Escobar-Jiménez RF (2022) Artificial neural networks: a practical review of applications involving fractional calculus. Eur Phys J Spec Top. https://doi.org/10.1140/epjs/s11734-022-00455-3

    Article  Google Scholar 

  13. Wang J, Yang G, Zhang B, Sun Z, Liu Y, Wang J (2017) Convergence analysis of Caputo-type fractional order complex-valued neural networks. IEEE Access 5:14560–14571. https://doi.org/10.1109/ACCESS.2017.2679185

    Article  Google Scholar 

  14. Chen M-R, Chen B-P, Zeng G-Q, Lu K-D, Chu P (2020) An adaptive fractional-order BP neural network based on extremal optimization for handwritten digits recognition. Neurocomputing 391:260–272. https://doi.org/10.1016/j.neucom.2018.10.090

    Article  Google Scholar 

  15. Anastassiou GA (2012) Fractional neural network approximation. Comput Math Appl 64(6):1655–1676. https://doi.org/10.1016/j.camwa.2012.01.019

    Article  MATH  Google Scholar 

  16. Khan S, Ahmad J, Naseem I, Moinuddin M (2018) A novel fractional gradient-based learning algorithm for recurrent neural networks. Circuits Syst Sig Process 37(2):593–612. https://doi.org/10.1007/s00034-017-0572-z

    Article  MATH  Google Scholar 

  17. Chen Y, Zhao G (2019) A Caputo-type fractional-order gradient descent learning of deep BP neural networks. In: 2019 IEEE 3rd advanced information management, communicates, electronic and automation control conference (IMCEC), pp 546–550. IEEE. https://doi.org/10.1109/IMCEC46724.2019.8984089. https://ieeexplore.ieee.org/document/8984089/

  18. Zuñiga Aguilar CJ, Gómez-Aguilar JF, Alvarado-Martínez VM, Romero-Ugalde HM (2020) Fractional order neural networks for system identification. Chaos Solitons Fractals 130:109444. https://doi.org/10.1016/j.chaos.2019.109444

    Article  MATH  Google Scholar 

  19. Pu Y-F, Yi Z, Zhou J-L (2017) Fractional Hopfield neural networks: fractional dynamic associative recurrent neural networks. IEEE Trans Neural Netw Learn Syst 28(10):2319–2333. https://doi.org/10.1109/TNNLS.2016.2582512

    Article  Google Scholar 

  20. PU Y-F, Wang J (2019) Fractional-order backpropagation neural networks: modified fractional-order steepest descent method for family of backpropagation neural networks arXiv:1906.09524

  21. Sharafian A, Ghasemi R (2019) Fractional neural observer design for a class of nonlinear fractional chaotic systems. Neural Comput Appl 31(4):1201–1213. https://doi.org/10.1007/s00521-017-3153-y

    Article  Google Scholar 

  22. Yang Z, Zhang J, Hu J, Mei J (2021) New results on finite-time stability for fractional-order neural networks with proportional delay. Neurocomputing 442:327–336. https://doi.org/10.1016/j.neucom.2021.02.082

    Article  Google Scholar 

  23. Yu Z, Sun G, Lv J (2022) A fractional-order momentum optimization approach of deep neural networks. Neural Comput Appl. https://doi.org/10.1007/s00521-021-06765-2

    Article  Google Scholar 

  24. Barron AR (1994) Approximation and estimation bounds for artificial neural networks. Mach Learn. https://doi.org/10.1007/bf00993164

    Article  MATH  Google Scholar 

  25. Ziegel ER (2003) The elements of statistical learning. Technometrics 45(3):267–268. https://doi.org/10.1198/tech.2003.s770

    Article  Google Scholar 

  26. Haykin S (1999) Neural networks: a comprehensive foundation (3rd Edn)

  27. Candès EJ (1999) Harmonic analysis of neural networks. Appl Comput Harmonic Anal. https://doi.org/10.1006/acha.1998.0248

    Article  MATH  Google Scholar 

  28. Muayad A, Irtefaa AN (2016) Ridge regression using artificial neural network. Indian J Sci Technol 9(31):1–5. https://doi.org/10.17485/ijst/2016/v9i31/84278

    Article  Google Scholar 

  29. Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R (2014) Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res 15:1929–1958

    MATH  Google Scholar 

  30. Cavazza J, Haeffele BD, Lane C, Morerio P, Murino V, Vidal R (2018) Dropout as a low-rank regularizer for matrix factorization. In: international conference on artificial intelligence and statistics, AISTATS 2018, pp 435–444

  31. Rumelhart DE, Hinton GE, Williams RJ (1986) Learning internal representations by error propagation. In: Rumenhart D, McCelland J (eds) Explorations in the micro-structure of cognition, vol 1, Foundations (Rumenhart edn), pp 318–362. MIT Press, Cambridge

  32. Hoerl AE, Kennard RW (1970) Ridge regression: biased estimation for nonorthogonal problems. Technometrics 12(1):55–67. https://doi.org/10.1080/00401706.1970.10488634

    Article  MATH  Google Scholar 

  33. Jarad F, Uğurlu E, Abdeljawad T, Baleanu D (2017) On a new class of fractional operators. Adv Differ Equ 2017(1):247. https://doi.org/10.1186/s13662-017-1306-z

    Article  MATH  Google Scholar 

  34. Wang H, Yu Y, Wen G (2014) Stability analysis of fractional-order Hopfield neural networks with time delays. Neural Netw 55:98–109. https://doi.org/10.1016/j.neunet.2014.03.012

    Article  MATH  Google Scholar 

  35. Verhulst P-F (2009) Notice sur la loi que la population poursuit dans son accroissement. Correspondance mathématique et physique 10: 113–121. Technical report, retrieved on 09/08

  36. Dugas C, Bengio Y, Bélisle F, Nadeau C, Garcia R (2001) Incorporating second-order functional knowledge for better option pricing. In: advances in neural information processing systems

  37. Ramachandran P, Zoph B, Le QV (2017) Searching for activation functions arXiv:1710.05941

  38. Mhaskar HN, Micchelli CA (1994) How to choose an activation function. In: Advances in Neural Information Processing Systems, pp 319–326

  39. Nwankpa C, Ijomah W, Gachagan A, Marshall S (2018) Activation functions: comparison of trends in practice and research for deep learning arXiv:1811.03378

  40. LeCun Y, Cortes C (2010) MNIST handwritten digit database. AT &T Labs [Online]. Available: http://yann. lecun. com/exdb/mnist

  41. Fisher RA (2021) Iris data set, UCI repository of machine learning databases. https://archive.ics.uci.edu/ml/datasets/iris

  42. DeLong ER, DeLong DM, Clarke-Pearson DL (1988) Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 44(3):837. https://doi.org/10.2307/2531595

    Article  MATH  Google Scholar 

  43. Krizhevsky A, Sutskever I, Hinton GE (2012) ImageNet classification with deep convolutional neural networks. In: advances in neural information processing systems

  44. Simonyan K, Zisserman A (2015) Very deep convolutional networks for large-scale image recognition. In: 3rd international conference on learning representations, ICLR 2015 - Conference track proceedings

Download references

Funding

Not applicable.

Author information

Author notes

    Authors and Affiliations

    1. Computer Engineering Department, Iskenderun Technical University, 31200, Iskenderun, Hatay, Türkiye

      Gokhan Altan & Sertan Alkan

    2. Physics Department, Cankaya University, 06790, Etimesgut, Ankara, Türkiye

      Dumitru Baleanu

    Authors
    1. Gokhan Altan
      View author publications

      You can also search for this author inPubMed Google Scholar

    2. Sertan Alkan
      View author publications

      You can also search for this author inPubMed Google Scholar

    3. Dumitru Baleanu
      View author publications

      You can also search for this author inPubMed Google Scholar

    Contributions

    The idea for the article was from Gokhan Altan, the literature search was performed by GA and SA, and SA drafted the proportional derivative. DB critically revised the work.

    Corresponding author

    Correspondence to Gokhan Altan.

    Ethics declarations

    Conflict of interest

    The authors declare that they have no conflict of interest.

    Ethics approval

    Not applicable.

    Consent to participate

    Not applicable.

    Consent for publication

    Not applicable.

    Additional information

    Publisher's Note

    Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

    Sertan Alkan and Dumitru Baleanu have contributed equally to this work.

    Rights and permissions

    Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

    Reprints and permissions

    About this article

    Check for updates. Verify currency and authenticity via CrossMark

    Cite this article

    Altan, G., Alkan, S. & Baleanu, D. A novel fractional operator application for neural networks using proportional Caputo derivative. Neural Comput & Applic 35, 3101–3114 (2023). https://doi.org/10.1007/s00521-022-07728-x

    Download citation

    • Received:

    • Accepted:

    • Published:

    • Issue Date:

    • DOI: https://doi.org/10.1007/s00521-022-07728-x

    Keywords