Skip to main content

Advertisement

Springer Nature Link
Log in

Linear normalization attention neural Hawkes process

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

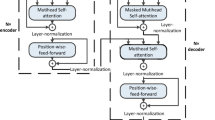
With the development of the Internet and the formal arrival of the era of big data, people record, store and process data in electronic form, while the bulk of the data in the real life are asynchronous event sequence data. For modeling the asynchronous event sequence, neural point process is one of the most mainstream solutions. With the more and more in-depth study of neural point process, in order to boost the prediction accuracy of the model, the complexity of the model cannot be overestimated, or the selected model itself has more nonlinearity. For example, the neural point process based on attention mechanism will lead to great complexity of the model. Meanwhile, with the development of deep learning, people find that the traditional multi-layer perceptron has great potential. Now many model architectures built with pure multi-layer perceptron without attention have been proposed, and the effect is better than the attention mechanism. Therefore, the multi-layer perceptron has been "reborn" and has attracted extensive attention. Inspired by this, we propose the Linear Normalization Attention Hawkes Process (LNAHP), which substitutes the multi-head dot-product attention from the transformer for linear normalization attention, and learns the hidden representation through two linear transformation layers and normalization operation, which markedly reduces the complexity of the model. The performance for different evaluation metrics for the LNAHP is verified and compared to the current baselines on real datasets from different fields and synthetic datasets, which proves the effectiveness of the LNAHP.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Dubey M, Palakkadavath R, Srijith PK (2021) Bayesian neural Hawkes process for event uncertainty prediction. arXiv preprint arXiv:2112.14474

  2. Bacry E, Dayri K, Muzy JF (2012) Non-parametric kernel estimation for symmetric Hawkes processes. Application to high frequency financial data. Eur Phys J B 85(5):1–12

    Article  Google Scholar 

  3. Aït-Sahalia Y, Cacho-Diaz J, Laeven RJA (2015) Modeling financial contagion using mutually exciting jump processes. J Financ Econ 117(3):585–606

    Article  Google Scholar 

  4. Reynaud-Bouret P, Schbath S (2010) Adaptive estimation for Hawkes processes; application to genome analysis. Ann Stat 38(5):2781–2822

    Article  MathSciNet  MATH  Google Scholar 

  5. Mohler GO, Short MB, Brantingham PJ et al (2011) Self-exciting point process modeling of crime. J Am Stat Assoc 106(493):100–108

    Article  MathSciNet  MATH  Google Scholar 

  6. Ogata Y (1999) Seismicity analysis through point-process modeling: a review. Seismicity patterns, their statistical significance and physical meaning. Science 8:471–507

    Google Scholar 

  7. Zhou F, Kong Q, Zhang Y, Feng C, Zhu J (2021) Nonlinear Hawkes processes in time-varying system. arXiv preprint arXiv:2106.04844

  8. Wang L, Zhang W, He X et al. (2018) Supervised reinforcement learning with recurrent neural network for dynamic treatment recommendation. In: Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery and data mining, pp 2447–2456

  9. Zhou K, Zha H, Song L (2013) Learning social infectivity in sparse low-rank networks using multi-dimensional Hawkes processes. Artif Intell Stat PMLR 2013:641–649

    Google Scholar 

  10. Errais E, Giesecke K, Goldberg LR (2010) Affine point processes and portfolio credit risk. SIAM J Financ Math 1(1):642–665

    Article  MathSciNet  MATH  Google Scholar 

  11. Daley DJ, Vere-Jones D (2003) An introduction to the theory of point processes: volume I: elementary theory and methods. Springer, New York

    MATH  Google Scholar 

  12. Cox DR, Isham V (1980) Point processes. CRC Press, London

    MATH  Google Scholar 

  13. Lewis PAW (1964) A branching Poisson process model for the analysis of computer failure patterns. J Roy Stat Soc Ser B (Methodol) 26(3):398–441

    MathSciNet  MATH  Google Scholar 

  14. Hawkes AG (1971) Spectra of some self-exciting and mutually exciting point processes. Biometrika 58(1):83–90

    Article  MathSciNet  MATH  Google Scholar 

  15. Liniger TJ (2009) Multivariate Hawkes processes. ETH Zurich, New York

    Google Scholar 

  16. Hewlett P (2006) Clustering of order arrivals, price impact and trade path optimization. Workshop on financial modeling with jump processes. Ecole Polytechnique. 5:6–8

    Google Scholar 

  17. Bacry E, Mastromatteo I, Muzy JF (2015) Hawkes processes in finance. Market Microstruct Liq 1(01):1550005

    Article  Google Scholar 

  18. Embrechts P, Liniger T, Lin L (2011) Multivariate Hawkes processes: an application to financial data. J Appl Probab 48(A):367–378

    Article  MathSciNet  MATH  Google Scholar 

  19. Large J (2007) Measuring the resiliency of an electronic limit order book. J Financ Mark 10(1):1–25

    Article  Google Scholar 

  20. Gusto G, Schbath S (2005) FADO: a statistical method to detect favored or avoided distances between occurrences of motifs using the Hawkes’ model. Stat Appl Genet Mol Biol 4(1):889

    Article  MathSciNet  MATH  Google Scholar 

  21. Johnson SD, Bernasco W, Bowers KJ et al (2007) Space–time patterns of risk: a cross national assessment of residential burglary victimization. J Quant Criminol 23(3):201–219

    Article  Google Scholar 

  22. Vere-Jones D, Davies RB (1966) A statistical survey of earthquakes in the main seismic region of New Zealand: part 2—time series analyses. NZ J Geol Geophys 9(3):251–284

    Article  Google Scholar 

  23. Vere-Jones D (1970) Stochastic models for earthquake occurrence. J R Stat Soc Ser B (Methodol) 32(1):1–45

    MathSciNet  MATH  Google Scholar 

  24. Hu J, Perer A, Wang F (2016) Data driven analytics for personalized healthcare. Healthcare information management systems. Springer, Cham, pp 529–554

    Google Scholar 

  25. Sun L, Liu C, Guo C, et al. (2016) Data-driven automatic treatment regimen development and recommendation. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, pp 1865–1874

  26. Goyal A, Bonchi F, Lakshmanan LVS (2010) Learning influence probabilities in social networks. In: Proceedings of the third ACM international conference on Web search and data mining, pp 241–250

  27. Zhao Q, Erdogdu MA, He HY et al. (2015) Seismic: a self-exciting point process model for predicting tweet popularity. In: Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining, pp 1513–1522

  28. Kobayashi R, Lambiotte R (2016) Tideh: time-dependent Hawkes process for predicting retweet dynamics. In: Proceedings of the international AAAI conference on web and social media, vol 10, no 1

  29. Zhou K, Zha H, Song L (2013) Learning social infectivity in sparse low-rank networks using multi-dimensional Hawkes processes. Artif Intell Stat PMLR 5:641–649

    Google Scholar 

  30. Myers S, Leskovec J (2010) On the convexity of latent social network inference. Adv Neural Inform Process Syst 23:5566

    Google Scholar 

  31. Giesecke K, Goldberg LR, Ding X (2011) A top-down approach to multiname credit. Oper Res 59(2):283–300

    Article  MathSciNet  MATH  Google Scholar 

  32. Cryer JD (1986) Time series analysis. Duxbury Press, Boston

    MATH  Google Scholar 

  33. Soderland S, Kim G L, Hawkins N (xxxx) A language model for extracting implicit relations

  34. Hirschberg J, Manning CD (2015) Advances in natural language processing. Science 349(6245):261–266

    Article  MathSciNet  MATH  Google Scholar 

  35. Chung J, Gulcehre C, Cho KH et al. (2010) Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:1412.3555

  36. Johnson R, Zhang T (2015) Semi-supervised convolutional neural networks for text categorization via region embedding. Adv Neural Inform Process Syst 28:888

    Google Scholar 

  37. Nguyen TH, Grishman R (2015) Relation extraction: perspective from convolutional neural networks. In: Proceedings of the 1st workshop on vector space modeling for natural language processing, pp 39–48

  38. Vaswani A, Shazeer N, Parmar N et al (2017) Attention is all you need. Adv Neural Inform Process Syst 2:30

    Google Scholar 

  39. Du N, Dai H, Trivedi R et al. (2016) Recurrent marked temporal point processes: Embedding event history to vector. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, pp 1555–1564

  40. Xiao S, Yan J, Yang X et al. (2018) Modeling the intensity function of point process via recurrent neural networks. In: Proceedings of the AAAI conference on artificial intelligence, vol 31, no 1

  41. Mei H, Eisner JM (2017) The neural Hawkes process: a neurally self-modulating multivariate point process. Adv Neural Inform Process Syst 2:30

    Google Scholar 

  42. Zhang Q, Lipani A, Kirnap O et al. (2020) Self-attentive Hawkes process. In: International conference on machine learning. PMLR, pp 11183–11193

  43. Zuo S, Jiang H, Li Z et al. (2020) Transformer Hawkes process. In: International conference on machine learning. PMLR, pp 11692–11702

  44. Zhang L, Liu J, Song Z et al. (2021) Universal transformer Hawkes process. In: 2021 international joint conference on neural networks (IJCNN). IEEE, pp 1–7

  45. Joseph S, Kashyap LD, Jain S (2020) Shallow Neural Hawkes: Non-parametric kernel estimation for Hawkes processes. arXiv preprint arXiv:2006.02460

  46. Tolstikhin IO, Houlsby N, Kolesnikov A et al. (2021) Mlp-mixer: an all-mlp architecture for vision. In: Advances in neural information processing systems, pp 34

  47. Melas-Kyriazi L (2021) Do you even need attention? a stack of feed-forward layers does surprisingly well on imagenet. arXiv preprint arXiv:2105.02723

  48. Ding X, Xia C, Zhang X et al. (2021) Repmlp: re-parameterizing convolutions into fully-connected layers for image recognition. arXiv preprint arXiv:2105.01883

  49. Gallager RG (1996) Poisson processes. Discrete stochastic processes. Springer, Boston, pp 31–55

    Google Scholar 

  50. Pemantle R (2007) A survey of random processes with reinforcement. Probab Surv 4:1–79

    Article  MathSciNet  MATH  Google Scholar 

  51. Isham V, Westcott M (1979) A self-correcting point processes. Stochastic Process Appl 8(3):335–347

    Article  MATH  Google Scholar 

  52. Zhou K, Zha H, Song L (2013) Learning triggering kernels for multi-dimensional Hawkes processes. In: International conference on machine learning. PMLR, pp 1301–1309

  53. Malaviya J (2021) Survey on modeling intensity function of Hawkes process using neural models. arXiv preprint arXiv:2104.11092

  54. Dehghani M, Gouws S, Vinyals O et al. (2018) Universal transformers. arXiv preprint arXiv:1807.03819

  55. Dai Z, Yang Z, Yang Y et al. (2019) Transformer-xl: Attentive language models beyond a fixed-length context. arXiv preprint arXiv:1901.02860

  56. Guo MH, Liu ZN, Mu TJ et al. (2021) Beyond self-attention: external attention using two linear layers for visual tasks. arXiv preprint arXiv:2105.02358

  57. Krizhevsky A, Sutskever I, Hinton GE (2012) Imagenet classification with deep convolutional neural networks. Adv Neural Inform Process Syst 25:889

    Google Scholar 

  58. Ba JL, Kiros JR, Hinton GE (2016) Layer normalization. arXiv preprint arXiv:1607.06450

  59. He K, Zhang X, Ren S et al. (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 770–778

  60. Ozaki T (1979) Maximum likelihood estimation of Hawkes’ self-exciting point processes. Ann Inst Stat Math 31(1):145–155

    Article  MathSciNet  MATH  Google Scholar 

  61. Xu H, Farajtabar M, Zha H (2016) Learning granger causality for Hawkes processes. In: International conference on machine learning. PMLR, pp 1717–1726

  62. Hochreiter S, Schmidhuber J (1997) Long short-term memory. Neural Comput 9(8):1735–1780

    Article  Google Scholar 

  63. Kingma D P, Ba J (2014) Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980

  64. Hildebrand FB (1987) Introduction to numerical analysis. Courier Corporation, London

    MATH  Google Scholar 

  65. Robert CP, Casella G, Casella G (1999) Monte Carlo statistical methods. Springer, New York

    Book  MATH  Google Scholar 

  66. Johnson AEW, Pollard TJ, Shen L et al (2016) MIMIC-III, a freely accessible critical care database. Scientific data 3(1):1–9

    Article  Google Scholar 

  67. Leskovec J, Krevl A (2014) SNAP datasets: Stanford large network dataset collection

Download references

Author information

Authors and Affiliations

  1. Department of Automation, College of Information Science and Engineering, China University of Petroleum, Beijing, Beijing, China

    Zhi-yan Song, Jian-wei Liu, Jie Yang & Lu-ning Zhang

Authors
  1. Zhi-yan Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jian-wei Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jie Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Lu-ning Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jian-wei Liu.

Ethics declarations

Conflict of interest

We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work, there is no professional or other personal interest of any nature or kind in any product, service and/or company that could be construed as influencing the position presented in, or the review of, the manuscript entitled “Linear Normalization Attention Neural Hawkes Process.”

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, Zy., Liu, Jw., Yang, J. et al. Linear normalization attention neural Hawkes process. Neural Comput & Applic 35, 1025–1039 (2023). https://doi.org/10.1007/s00521-022-07821-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07821-1

Keywords