Skip to main content

Advertisement

Springer Nature Link
Log in

DH-GAC: deep hierarchical context fusion network with modified geodesic active contour for multiple neurofibromatosis segmentation

  • S.I.: Efficient Artificial Intelligent Algorithms for Medical Image Analysis Based on High-Performance Computing
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

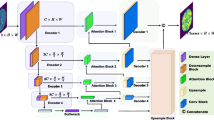
Delineating accurately and simultaneously all lesions is vital and challenging for computer-aided diagnosis for multiple neurofibromatosis (NF). However, existing CNN-based segmentation methods paid little attention to weak boundaries. Moreover, due to the intensity-inhomogeneous distribution of medical images, the ambiguous boundaries, and highly variable locations, sizes and shapes of the lesions, delineating multiple lesions simultaneously remains quite challenging. To address these challenges, we introduce a novel end-to-end segmentation framework of multiple NF, deep hierarchical geodesic active contour (DH-GAC). It leverages the elaborately designed deep hierarchical context fusion network (DH-CFN) to improve the generalization and robustness of DH-GAC, and the modified geodesic active contour (MGAC) to delineate precisely all lesions as much as possible. Specifically, it employs DH-CFN to predict specific parameter maps of each image for MGAC and feeds them into the energy function of MGAC to delineate NF lesions, which makes DH-GAC end-to-end trainable. Moreover, to improve the generalization of DH-GAC, we adopt two different settings to initialize the surface for DH-GAC. Experimental results demonstrate that DH-GAC not only improves the segmentation precision, but also overcomes the intrinsic drawback of classical geodesic active contour in boundary delineation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The data that support the findings of this study are available from Harvard Medical School but restrictions apply to the availability of these data, which were used under licence for the current study, and so are not publicly available. Data are however available from the last author upon reasonable request and with permission of Harvard Medical School.

References

  1. Otsu N (1975) A threshold selection method from gray-level histogram. Automatica 11:285–296

    MATH  Google Scholar 

  2. Saleh S, Kalyankar NV, Khamitkar S (2010) Image segmentation by using threshold techniques. J Comput 2(5):2151–9617

    Google Scholar 

  3. Adams R, Bischof L (1994) Seeded region growing. IEEE Trans Pattern Anal Mach Intell 16:641–647. https://doi.org/10.1109/34.295913

    Article  MATH  Google Scholar 

  4. Boykov YY, Jolly M-P (2001) Interactive graph cuts for optimal boundary region segmentation of objects in n-d images. In: Proceedings Eighth IEEE International Conference on Computer Vision. ICCV 2001, vol 1, pp 105–112. https://doi.org/10.1109/ICCV.2001.937505

  5. Rother C, Kolmogorov V, Blake A (2004) Grabcut: interactive foreground extraction using iterated graph cuts. ACM Trans Graph 23:309–314. https://doi.org/10.1145/1186562.1015720

    Article  MATH  Google Scholar 

  6. Felzenszwalb P, Huttenlocher D (2004) Efficient graph-based image segmentation. Int J Comput Vis 59:167–181. https://doi.org/10.1023/B:VISI.0000022288.19776.77

    Article  MATH  Google Scholar 

  7. Kass M, Witkin A, Terzopoulos D (1988) Snakes: active contour models. Int J Comput Vis 1(4):321–331. https://doi.org/10.1016/B978-0-12-386454-3.00786-7

    Article  MATH  Google Scholar 

  8. Cohen LD (1991) On active contour models and balloons. CVGIP: Image Underst 53(2):211–218

    Article  MATH  Google Scholar 

  9. Xu C, Prince JL (1998) Snakes, shapes, and gradient vector flow. IEEE Trans Image Process 7(3):359–369. https://doi.org/10.1109/83.661186

    Article  MathSciNet  MATH  Google Scholar 

  10. Xu C, Prince J (2000) Generalized gradient vector flow external forces for active contours. Signal Process 71:131–139. https://doi.org/10.1016/S0165-1684(98)00140-6

    Article  MATH  Google Scholar 

  11. Jifeng N, Chengke W, Shigang L, Shuqin Y (2007) NGVF: an improved external force field for active contour model. Pattern Recogn Lett 28(1):58–63. https://doi.org/10.1016/j.patrec.2006.06.014

    Article  Google Scholar 

  12. Jia X, Wang Y (2009) An edge preserving gradient vector flow for active contours. In: Proceedings of the 2009 2nd International Congress on Image and Signal Processing, CISP’09. https://doi.org/10.1109/CISP.2009.5304695

  13. Wang Y, Liu L, Zhang H, Cao Z, Lu S (2010) Image segmentation using active contours with normally biased gvf external force. IEEE Signal Process Lett 17(10):875–878. https://doi.org/10.1109/LSP.2010.2060482

    Article  MATH  Google Scholar 

  14. Yao Y, Liu L, Liao L, Wei M, Guo J, Li Y (2012) Sigmoid gradient vector flow for medical image segmentation. Int Conf Signal Process Proc ICSP 2(2):881–884. https://doi.org/10.1109/ICoSP.2012.6491721

    Article  MATH  Google Scholar 

  15. Osher S, Sethian J (1988) Fronts propagating with curvature dependent speed algorithms based on hamilton-jacobi. J Comput Phys 79:12–49. https://doi.org/10.1016/0021-9991(88)90002-2

    Article  MathSciNet  MATH  Google Scholar 

  16. Caselles V, Kimmel R, Sapiro G (1997) Geodesic active contours. Int J Comput Vis 22(1):61–79. https://doi.org/10.1023/A:1007979827043

    Article  MATH  Google Scholar 

  17. Goldenberg R, Kimmel R, Rivlin E, Rudzsky M (2001) Fast geodesic active contours. IEEE Trans Image Process 10(10):1467–1475. https://doi.org/10.1109/83.951533

    Article  MathSciNet  MATH  Google Scholar 

  18. Paragios N, Mellina-Gottardo O, Ramesh V (2004) Gradient vector flow fast geometric active contours. IEEE Trans Pattern Anal Mach Intell 26(3):402–407. https://doi.org/10.1109/TPAMI.2004.1262337

    Article  Google Scholar 

  19. Chan TF, Vese LA (2001) Active contours without edges. IEEE Trans Image Process 10(2):266–277. https://doi.org/10.1109/83.902291

    Article  MATH  Google Scholar 

  20. Li C, Kao C, Gore JC, Ding Z (2007) Implicit active contours driven by local binary fitting energy. In: 2007 IEEE Conference on Computer Vision and Pattern Recognition, pp 1–7. https://doi.org/10.1109/CVPR.2007.383014

  21. Feng C (2017) IEOPF: An active contour model for image segmentation with inhomogeneities estimated by orthogonal primary functions

  22. Li C, Huang R, Ding Z, Gatenby JC, Metaxas DN, Gore JC (2011) A level set method for image segmentation in the presence of intensity inhomogeneities with application to mri. IEEE Trans Image Process 20(7):2007–2016. https://doi.org/10.1109/TIP.2011.2146190

    Article  MathSciNet  MATH  Google Scholar 

  23. Li X, Liu H, Xing Y (2019) A hybride active contour model driven by global and local image information. Neural Process Lett. https://doi.org/10.1007/s11063-019-10004-0

    Article  MATH  Google Scholar 

  24. Tan G, Guo Z, Xiao Y (2019) PA-RetinaNet: path augmented retinaNet for dense object detection, pp. 138–149. https://doi.org/10.1007/978-3-030-30484-3_12

  25. Chen C, Li K, Zou X, Zhongyao C, Wei W, Tian Q, Zeng Z (2021) Hierarchical semantic graph reasoning for train component detection. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2021.3057792

    Article  MATH  Google Scholar 

  26. Wu X, Tan G, Zhu N, Chen Z, Yang Y, Wen H, Li K (2021) Cachetrack-yolo: Real-time detection and tracking for thyroid nodules and surrounding tissues in ultrasound videos. IEEE J Biomed Health Inform 25(10):3812–3823. https://doi.org/10.1109/JBHI.2021.3084962

    Article  Google Scholar 

  27. Shelhamer E, Long J, Darrell T (2017) Fully convolutional networks for semantic segmentation. IEEE Trans Pattern Anal Mach Intell 39(4):640–651. https://doi.org/10.1109/TPAMI.2016.2572683

    Article  MATH  Google Scholar 

  28. Badrinarayanan V, Kendall A, Cipolla R (2017) Segnet: a deep convolutional encoder-decoder architecture for image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence 39(12):2481–2495. https://doi.org/10.1109/TPAMI.2016.2644615

  29. Ronneberger O, Fischer P, Brox T (2015) U-net: convolutional networks for biomedical image segmentation. In: Lecture notes in computer science (including subseries lecture notes in artificial intelligence and lecture notes in bioinformatics) 9351:234–241. https://doi.org/10.1007/978-3-319-24574-4_28

  30. Chen L-C, Papandreou G, Kokkinos I, Murphy K, Yuille AL (2018) Deeplab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans Pattern Anal Mach Intell 40(4):834–848. https://doi.org/10.1109/TPAMI.2017.2699184

    Article  MATH  Google Scholar 

  31. Zhou Z, Rahman Siddiquee MM, Tajbakhsh N, Liang J (2018) Unet++: A nested u-net architecture for medical image segmentation. In: Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, pp 3–11. Springer, Cham. https://doi.org/10.1007/978-3-030-00889-5_1

  32. He K, Gkioxari G, Dollár P, Girshick R (2017) Mask r-cnn. In: 2017 IEEE International Conference on Computer Vision (ICCV), pp. 2980–2988. https://doi.org/10.1109/ICCV.2017.322

  33. Wu X, Tan G, Li K, Li S, Wen H, Zhu X, Cai W (2020) Deep parametric active contour model for neurofibromatosis segmentation. Future Gener Comput Syst 112:58–66. https://doi.org/10.1016/j.future.2020.05.001

    Article  MATH  Google Scholar 

  34. Cai Z, Vasconcelos N (2021) Cascade r-cnn: high quality object detection and instance segmentation. IEEE Trans Pattern Anal Mach Intell 43(5):1483–1498. https://doi.org/10.1109/TPAMI.2019.2956516

    Article  MATH  Google Scholar 

  35. Peng S, Jiang W, Pi H, Li X, Bao H, Zhou X (2020) Deep snake for real-time instance segmentation. In: 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 8530–8539. https://doi.org/10.1109/CVPR42600.2020.00856

  36. Ranjbarzadeh R, Bagherian Kasgari A, Jafarzadeh Ghoushchi S, Anari S, Naseri M, Bendechache M (2021) Brain tumor segmentation based on deep learning and an attention mechanism using mri multi-modalities brain images. Sci Rep 11:567–577. https://doi.org/10.1038/s41598-021-90428-8

    Article  Google Scholar 

  37. Jin Q, Cui H, Sun C, Meng Z, Su R (2021) Cascade knowledge diffusion network for skin lesion diagnosis and segmentation. Appl Soft Comput 99:106881. https://doi.org/10.1016/j.asoc.2020.106881

    Article  Google Scholar 

  38. Chen C, Li K, Wei W, Zhou J, Zeng Z (2021) Hierarchical graph neural networks for few-shot learning. IEEE Trans Circ Syst Video Technol. https://doi.org/10.1109/TCSVT.2021.3058098

    Article  MATH  Google Scholar 

  39. Pu B, Zhu N, Li K, Li S (2021) Fetal cardiac cycle detection in multi-resource echocardiograms using hybrid classification framework. Future Gener Comput Syst 115:825–836. https://doi.org/10.1016/j.future.2020.09.014

    Article  MATH  Google Scholar 

  40. Pu B, Li K, Li S, Zhu N (2021) Automatic fetal ultrasound standard plane recognition based on deep learning and iiot. IEEE Trans Ind Inf 17(11):7771–7780. https://doi.org/10.1109/TII.2021.3069470

    Article  MATH  Google Scholar 

  41. Chen J, Li K, Li K, Yu P, Zeng Z (2021) Dynamic planning of bicycle stations in dockless public bicycle-sharing system using gated graph neural network. ACM Trans Intell Syst Technol 12:1–22. https://doi.org/10.1145/3446342

    Article  MATH  Google Scholar 

  42. Chen J, Li K, Tang Z, Bilal K, Yu S, Weng C, Li K (2017) A parallel random forest algorithm for big data in a spark cloud computing environment. IEEE Trans Parallel Distrib Syst 28(4):919–933. https://doi.org/10.1109/TPDS.2016.2603511

    Article  MATH  Google Scholar 

  43. Rupprecht C, Huaroc E, Baust M, Navab N (2016) Deep active contours. https://arxiv.org/abs/1607.05074

  44. Chen H, Qi X, Yu L, Heng P-A (2016) Dcan: Deep contour-aware networks for accurate gland segmentation. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2487–2496. https://doi.org/10.1109/CVPR.2016.273

  45. Bai M, Urtasun R (2017) Deep watershed transform for instance segmentation. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2858–2866. https://doi.org/10.1109/CVPR.2017.305

  46. Kristiadi A (2017) Pranowo: deep convolutional level set method for image segmentation. J ICT Res Appl 11(3):284–298. https://doi.org/10.5614/itbj.ict.res.appl.2017.11.3.5

    Article  Google Scholar 

  47. Hu P, Shuai B, Liu J, Wang G (2017) Deep level sets for salient object detection. In: Proceedings - 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, pp 540–549. https://doi.org/10.1109/CVPR.2017.65

  48. Marcos D, Tuia D, Kellenberger B, Zhang L, Bai M, Liao R, Urtasun R (2018) Learning deep structured active contours end-to-end. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pp 8877–8885. https://doi.org/10.1109/CVPR.2018.00925

  49. Cheng D, Liao R, Fidler S, Urtasun R (2019) Darnet: Deep active ray network for building segmentation. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp 7423–7431. https://doi.org/10.1109/CVPR.2019.00761

  50. Cerrone L, Zeilmann A, Hamprecht FA (2019) End-to-end learned random walker for seeded image segmentation. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp 12551–12560. https://doi.org/10.1109/CVPR.2019.01284

  51. Hatamizadeh A, Hoogi A, Sengupta D, Lu W, Wilcox B, Rubin D, Terzopoulos D (2019) Deep active lesion segmentation. In: Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), pp 98–105. https://doi.org/10.1101/794529

  52. Hatamizadeh A, Sengupta D, Terzopoulos D (2020) End-to-end trainable deep active contour models for automated image segmentation: delineating buildings in aerial imagery. In: Computer Vision – ECCV 2020, pp 730–746. https://doi.org/10.1007/978-3-030-58610-2_43

  53. Chen X, Williams BM, Vallabhaneni SR, Czanner G, Williams R, Zheng Y (2019) Learning active contour models for medical image segmentation. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp 11624–11632. https://doi.org/10.1109/CVPR.2019.01190

  54. Kim Y, Kim S, Kim T, Kim C (2019) CNN-based semantic segmentation using level set loss. In: Proceedings - 2019 IEEE Winter Conference on Applications of Computer Vision, WACV 2019, pp 1752–1760. https://doi.org/10.1109/WACV.2019.00191

  55. Kim B, Ye JC (2020) Mumford-shah loss functional for image segmentation with deep learning. IEEE Trans Image Process 29:1856–1866. https://doi.org/10.1109/TIP.2019.2941265

    Article  MathSciNet  MATH  Google Scholar 

  56. Zhao X, Yin Y, Yang B, Zhu B, Tian X (2007) Level set and geodesic active contours based measurement of material removal between serial sections. Comput Mater Sci 39:857–861. https://doi.org/10.1016/j.commatsci.2006.10.018

    Article  MATH  Google Scholar 

  57. Caselles V, Catte F, Coll B, Dibos F (1993) A geometric model for active contours in image processing. Numer Math 66:1–31. https://doi.org/10.1007/BF01385685

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 62072168) and Natural Science Foundation of Hunan Province (Grant No. 2021JJ30148).

Author information

Authors and Affiliations

  1. College of Computer Science and Electronic Engineering, Hunan University, Lushan Road, Changsha, 410082, Hunan, China

    Xiangqiong Wu, Guanghua Tan, Bin Pu & Mingxing Duan

  2. Harvard Medical School, Harvard University, 25 Shattuck Street, Boston, MA, 02115, USA

    Wenli Cai

Authors
  1. Xiangqiong Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Guanghua Tan
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Bin Pu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Mingxing Duan
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Wenli Cai
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Conceptualization was contributed by XW, GT, and WC; methodology was contributed by GT and WC; formal analysis and investigation were contributed by XW; technical guidance was contributed by GT and WC; writing-original draft preparation was contributed by XW; writing-review and editing was contributed by BP and MD; funding acquisition was contributed by GT and WC; visualization was contributed by XW and BP; and resources were contributed by MD and WC.

Corresponding author

Correspondence to Guanghua Tan.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.

Ethical approval

The article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, X., Tan, G., Pu, B. et al. DH-GAC: deep hierarchical context fusion network with modified geodesic active contour for multiple neurofibromatosis segmentation. Neural Comput & Applic 37, 7511–7526 (2025). https://doi.org/10.1007/s00521-022-07945-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07945-4

Keywords