Skip to main content

Advertisement

Springer Nature Link
Log in

Generalized complex kernel least-mean-square algorithm with adaptive kernel widths

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

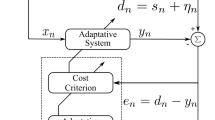
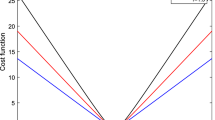
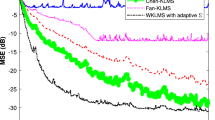
A novel variable kernel width generalized complex-valued least mean-square (VKW-GCKLMS) algorithm aims to optimize kernel width in online way to tackle with the problem that the performance of nonlinear kernel algorithms with fixed values of kernel widths is degraded by inappropriate choice of kernel widths. The proposed VKW-GCKLMS algorithm is able to continuously optimize values of kernel widths by using stochastic gradient algorithm in the task of complex-valued nonlinear filtering. Numerical simulations illustrate that the VKW-GCKLMS algorithm is capable of guiding values of kernel widths of different kernels toward those that can achieve the optimal filtering performances. In addition, it is also shown that initial values of kernel widths do not have evident effect on the filtering performance of the VKW-GCKLMS algorithm, which demonstrates the high effectiveness of the VKW-GCKLMS algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. Adali T, Schreier PJ, Scharf LL (2011) Complex-valued signal processing: the proper way to deal with impropriety. IEEE Trans on Signal Process 59(11):5101–5125. https://doi.org/10.1109/TSP.2011.2162954

    Article  MathSciNet  MATH  Google Scholar 

  2. Mandic DP, Goh VSL (2009) Complex valued nonlinear adaptive filters: noncircularity, widely linear and neural models. Wiley, New York. https://doi.org/10.1002/9780470742624

    Book  Google Scholar 

  3. Widrow B, McCool J, Ball M (1975) The complex LMS algorithm. Proc IEEE 63:719–720. https://doi.org/10.1109/PROC.1975.9807

    Article  Google Scholar 

  4. Bouboulis P, Theodoridis S, Mavroforakis M (2012) The augmented complex kernel LMS. IEEE Trans Signal Process 60(9):4962–4967. https://doi.org/10.1109/TSP.2012.2200479

    Article  MathSciNet  MATH  Google Scholar 

  5. Chaudhary NI, Aslam MS, Baleanu D et al (2020) Design of sign fractional optimization paradigms for parameter estimation of nonlinear Hammerstein systems. Neural Comput Appl 32:8381–8399. https://doi.org/10.1007/s00521-019-04328-0

    Article  Google Scholar 

  6. Zhang S, Zhang J, Zheng J, Zheng WX, So HC (2019) Widely linear complex-valued estimated-input lms algorithm for bias-compensated adaptive filtering with noisy measurements. IEEE Trans Signal Process 67(13):3592–3605. https://doi.org/10.1109/TSP.2019.2919412

    Article  MathSciNet  MATH  Google Scholar 

  7. Mandic DP, Kanna S, Douglas SC (2015) Mean square analysis of the CLMS and ACLMS for non-circular signals. Proc IEEE Int Conf Acoust Speech Signal Process 2:3531–3535. https://doi.org/10.1109/ICASSP.2015.7178628

    Article  Google Scholar 

  8. Shi YM, Huang L, Qian C, So HC (2015) Shrinkage linear and widely linear complex-valued least mean squares algorithms for adaptive beamforming. IEEE Trans Signal Process 63(1):119–131. https://doi.org/10.1109/TSP.2014.2367452

    Article  MathSciNet  MATH  Google Scholar 

  9. Menguc EC, Acir N (2017) An augmented complex-valued least-mean kurtosis algorithm for the filtering of noncircular signals. IEEE Trans Signal Process 66(2):438–448. https://doi.org/10.1109/TSP.2017.2768024

    Article  MathSciNet  MATH  Google Scholar 

  10. Kanna S, Talebi SP, Mandic DP (2014) Diffusion widely linear adaptive estimation of system frequency in distributed power grids. IEEE Int Energy Conf. https://doi.org/10.1109/ENERGYCON.2014.6850513

    Article  Google Scholar 

  11. Ogunfunmi T, Paul TK (2011) On the complex kernel-based adaptive filter. Proc IEEE Int Symp Circuits Syst. https://doi.org/10.1109/ISCAS.2011.5937800

    Article  MATH  Google Scholar 

  12. Raja MAZ, Chaudhary NI, Ahmed Z et al (2019) A novel application of kernel adaptive filtering algorithms for attenuation of noise interferences. Neural Comput Appl 31:9221–9240. https://doi.org/10.1007/s00521-019-04390-8

    Article  Google Scholar 

  13. Boloix-Tortosa R, Murillo-Fuentes JJ, Payán-Somet FJ, Pérez-Cruz F (2018) Complex Gaussian processes for regression. IEEE Trans Neural Netw Learn Syst 29(11):5499–5511. https://doi.org/10.1109/TNNLS.2018.2805019

    Article  MathSciNet  Google Scholar 

  14. Sadoghi Yazdi H, Modaghegh H, Pakdaman M (2012) Ordinary differential equations solution in kernel space. Neural Comput Appl 21:79–85. https://doi.org/10.1007/s00521-011-0621-7

    Article  Google Scholar 

  15. Liu YQ, Du X, Shen HL, Chen SJ (2021) Estimating generalized gaussian blur kernels for out-of-focus image deblurring. IEEE Trans Circuits Syst Video Technol 31(3):829–843. https://doi.org/10.1109/TCSVT.2020.2990623

    Article  Google Scholar 

  16. Liu W, Pokharel PP, Principe JC (2008) The kernel least-mean-square algorithm. IEEE Trans Signal Process 56(2):543–554. https://doi.org/10.1109/TSP.2007.907881

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu W, Príncipe JC, Haykin S (2008) Kernel adaptive filtering: a comprehensive introduction. Wiley, New York

    Google Scholar 

  18. Bouboulis P, Theodoridis S (2010) The complex Gaussian kernel LMS algorithm. Proc 20th Int Conf Artif Neural Netw II:11–20. https://doi.org/10.1007/978-3-642-15822-3_2

    Article  Google Scholar 

  19. Gao W, Chen J, Richard C, Bermudez JCM, Huang J (2015),Convergence analysis of the augmented complex klms algorithm with pre-tuned dictionary. iN: IEEE International conference on acoustics speech and signal processing (ICASSP), pp 2006–2010. https://doi.org/10.1109/ICASSP.2015.7178322

  20. Qing Z, Ni J, Li Z, Chen J (2021) Selective partial-update augmented complex-valued LMS algorithm and its performance analysis. Signal Process 188:108217. https://doi.org/10.1016/j.sigpro.2021.108217

    Article  Google Scholar 

  21. Boloix-Tortosa R, Murillo-Fuentes JJ, Tsaftaris SA (2019) The generalized complex kernel least-mean-square algorithm. IEEE Trans Signal Process 67(20):5213–5222. https://doi.org/10.1109/TSP.2019.2937289

    Article  MathSciNet  MATH  Google Scholar 

  22. Boloix-Tortosa R, Murillo-Fuentes JJ, Santos I, Perez-Cruz F (2017) Widely linear complex-valued kernel methods for regression. IEEE Trans Signal Process 65(19):5240–5248. https://doi.org/10.1109/TSP.2017.2726991

    Article  MathSciNet  MATH  Google Scholar 

  23. Fan H, Song Q, Shrestha SB (2015) Kernel online learning with adaptive kernel width. Neurocomputing 175:233–242. https://doi.org/10.1016/j.neucom.2015.10.055

    Article  Google Scholar 

  24. Zhao J, Zhang H, Zhang JA (2020) Gaussian kernel adaptive filters with adaptive kernel bandwidth. Signal Process 166:107270. https://doi.org/10.1016/j.sigpro.2019.107270

    Article  Google Scholar 

  25. Chen B, Liang J, Zheng N, Principe JC (2016) Kernel least mean square with adaptive kernel size. Neurocomputing 191:95–106. https://doi.org/10.1016/j.neucom.2016.01.004

    Article  Google Scholar 

  26. Racine J (1993) An efficient cross-validation algorithm for window width selection for nonparametric kernel regression. Commun Stat Simul Comput 22:1107–1114. https://doi.org/10.1080/03610919308813144

    Article  Google Scholar 

  27. An S, Liu W, Venkatesh S (2007) Fast cross-validation algorithms for least squares support vector machine and kernel ridge regression. Pattern Recognit 40:2154–2162. https://doi.org/10.1016/j.patcog.2006.12.015

    Article  MATH  Google Scholar 

  28. Warren W (1988) Density estimation for statistics and data analysis-by B. W. Silverman. J R Stat Soc 150(4):403–404

    Google Scholar 

  29. Gao W, Huang J, Han J, Zhang Q (2016) Theoretical convergence analysis of complex gaussian kernel LMS algorithm. J Syst Eng Electron 27(1):39–50 (CNKI:SUN:XTGJ.0.2016-01-006)

    Google Scholar 

  30. Chen B, Zhao S, Zhu P, Principe JC (2012) Quantized kernel least mean square algorithm. IEEE Trans Neural Netw Learn Syst 23(1):22–32. https://doi.org/10.1109/TNNLS.2011.2178446

    Article  Google Scholar 

  31. Bouboulis P, Theodoridis S (2011) Extension of Wirtinger’s calculus to reproducing kernel Hilbert spaces and the complex kernel LMS. IEEE Trans Signal Process 59(3):964–978. https://doi.org/10.1109/TSP.2010.2096420

    Article  MathSciNet  MATH  Google Scholar 

  32. Liu W, Park I, Principe JC (2009) An information theoretic approach of designing sparse kernel adaptive filters. IEEE Trans Neural Netw Learn Syst 20(12):1950–1961. https://doi.org/10.1109/TNN.2009.2033676

    Article  Google Scholar 

  33. Platt J (1991) A resource-allocating network for function interpolation. Neural Comput 3(2):213–225. https://doi.org/10.1162/neco.1991.3.2.213

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

This work was supported by National Key R &D Program of China (2022YFE0198900), National Natural Science Foundation of China (61771430) and Basic Public Welfare Research Project of Zhejiang Province in China (LGG18F030002).

Author information

Author notes

  1. Zezhen Huang and Hua Gao have contributed equally to this work.

Authors and Affiliations

  1. College of Computer Science, Zhejiang University of Technology, Hangzhou, 310014, Zhejiang, China

    Wei Huang, Zezhen Huang & Hua Gao

Authors
  1. Wei Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zezhen Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hua Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hua Gao.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, W., Huang, Z. & Gao, H. Generalized complex kernel least-mean-square algorithm with adaptive kernel widths. Neural Comput & Applic 35, 6423–6434 (2023). https://doi.org/10.1007/s00521-022-08022-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-08022-6

Keywords