An algorithm of nonnegative matrix factorization under structure constraints for image clustering

Abstract

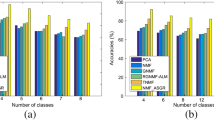
Nonnegative matrix factorization (NMF) is a crucial method for image clustering. However, NMF may obtain low accurate clustering results because the factorization results contain no data structure information. In this paper, we propose an algorithm of nonnegative matrix factorization under structure constraints (SNMF). The factorization results of SNMF could maintain data global and local structure information simultaneously. In SNMF, the global structure information is captured by the cosine measure under the $\ell _2$ norm constraints. Meanwhile, $\ell _2$ norm constraints are utilized to get more discriminant data representations. A graph regularization term is employed to maintain the local structure. Effective updating rules are given in this paper. Moreover, the effects of different normalizations on similarities are investigated through experiments. On real datasets, the numerical results confirm the effectiveness of the SNMF.

Appendix

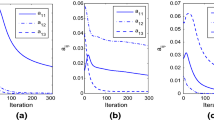
Because (18) and (19) are two gradient descent methods, (16) is non-increasing. Here is the proof.

Denote the objective function of (16) as F. The partial derivative of $U_{mk}$ in F is

$$\begin{aligned} \frac{\partial F}{\partial U_{mk}} = (-X^NV+UV^TV)_{mk}. \end{aligned}$$

(25)

The formulation of updating $U_{mk}$ through the gradient descent method is the following:

$$\begin{aligned} U_{mk}=U_{mk}+\tau _u(X^NV-UV^TV)_{mk}. \end{aligned}$$

(26)

When $\tau _u={U_{mk}}/{(UV^TV)_{mk}}$, the nonnegative constraints on U hold, and (26) is (18).

For V, the updating rule (19) is also a gradient descent method. The proof is similar to [25].

Let $x_r$ and h represent the ith row of V and $\frac{\partial F}{\partial x_r}$, respectively. Denote $F_1(x_r)$ as the related part of $x_r$ in (16). When omitting the nonnegative constraints, the Lagrange function of $x_r$ is the following:

$$\begin{aligned} L(x_r,\lambda )=F_1(x_r)+\frac{\lambda }{2}(x_rx_r^T-1). \end{aligned}$$

(27)

Denote

$$\begin{aligned} x=x_r^T, a=h^T,c_1=l_1^T,c_2=l_2^T. \end{aligned}$$

Rewrite (27) as follows:

$$\begin{aligned} L(x,\lambda )=F_1(x^T)+\frac{\lambda }{2}(x^Tx-1). \end{aligned}$$

(28)

When$\nabla _xL(x,\lambda )=0$, we have

$$\begin{aligned} a-x\lambda =0. \end{aligned}$$

Through the constraint $x^Tx=1$, we obtain

$$\begin{aligned} \lambda =x^Ta=a^Tx. \end{aligned}$$

Thus, rewrite $\nabla _xL(x,\lambda )$ as follows:

$$\begin{aligned} \begin{aligned} \nabla _xL(x,\lambda )&=a-x\lambda \\ \quad&=a-x^Tax \\ \quad&=ax^Tx-xa^Tx \\ \quad&=(ax^T-x^Ta)x \end{aligned} \end{aligned}$$

(29)

Let A represents $ax^T-xa^T$. Therefore, A is a skew-symmetric matrix. Since Ax is the gradient of (28) the updating rule in the gradient descent method of x should be the following:

$$\begin{aligned} y=x-\tau _vAx. \end{aligned}$$

However, it is difficult to satisfy the constraint $y^Ty=1$. From [33, 34], a modified method (30) is used.

$$\begin{aligned} y(\tau )=x-\tau A\left( \frac{x+y(\tau )}{2}\right) . \end{aligned}$$

(30)

(30) could satisfy that $y^Ty=x^Tx=1$ for any skew-symmetric matrix A and $\tau$.

From Lemma 1 (2) in [25], (30) could be expressed as:

$$\begin{aligned} y(\tau )=\left( I+\frac{\tau }{2}A\right) ^{-1}\left( I-\frac{\tau }{2}A\right) x. \end{aligned}$$

(31)

Then from Lemma 2 in [25], (31) could be rewritten as

$$\begin{aligned} y(\tau )=x-\beta _1(\tau )a-\beta _2(\tau )x, \end{aligned}$$

(32)

where

$$\begin{aligned} & \beta _1(\tau )=\tau \frac{x^Tx-\frac{\tau }{2}\left( (a^Tx)(x^Tx)-(x^Ta)(x^Tx)\right) }{1-\left( \frac{\tau }{2}\right) ^2(a^Tx)^2 +\left( \frac{\tau }{2}\right) ^2\Vert a\Vert ^2\Vert x\Vert ^2},\\ & \beta _2(\tau )=-\tau \frac{x^Ta-\frac{\tau }{2}\left( (a^Tx)(x^Ta)-(a^Ta)(x^Tx)\right) }{1-\left( \frac{\tau }{2}\right) ^2(a^Tx)^2 +\left( \frac{\tau }{2}\right) ^2\Vert a\Vert ^2\Vert x\Vert ^2}. \end{aligned}$$

The nonnegative constraints on y should be handled next.

Note $q=1-(\frac{\tau }{2})^2(a^Tx)^2+(\frac{\tau }{2})^2\Vert a\Vert ^2\Vert x\Vert ^2$. Rewrite (32) as follows:

$$\begin{aligned} y(\tau )=x-\frac{\tau }{q}(\beta _1^{'}(\tau )(c_1-c_2)+\beta _2^{'}x), \end{aligned}$$

(33)

where

$$\begin{aligned} & \beta _1^{'}(\tau )=x^Tx-\frac{\tau }{2}((a^Tx)(x^Tx)-(x^Ta)(x^Tx)),\\ & \beta _2^{'}(\tau )=x^Ta-\frac{\tau }{2}((a^Tx)(x^Ta)-(a^Ta)(x^Tx)). \end{aligned}$$

Expanding $\beta _1^{'}(\tau )(c_1-c_2)$ and $\beta _2^{'}x$ in (33) through auxiliary variables (6), we get

$$\begin{aligned} \begin{aligned} y(\tau )&=x-\frac{\tau }{q}\left( x^Txc_1+\frac{\tau }{2}T1+x^Tc_2x+\frac{\tau }{2}P1\right) \\ \quad&\quad +\frac{\tau }{q}\left( x^Txc_2+\frac{\tau }{2}T2+x^Tc_1x+\frac{\tau }{2}P2\right) . \end{aligned} \end{aligned}$$

(34)

Because $y(\tau )$ has nonnegative constraints, the $\tau$ should satisfy

$$\begin{aligned} x-\frac{\tau }{q}\left( x^Txc_1+\frac{\tau }{2}T1+x^Tc_2x+\frac{\tau }{2}P1\right) \ge 0. \end{aligned}$$

(35)

Denote $(a^Tx)^2-\Vert a\Vert ^2\Vert x\Vert ^2$ as M. Then $q=1-(\frac{\tau }{2})^2M$. Therefore, we obtain

$$\begin{aligned} & qx-\tau \left( x^Txc_1+\frac{\tau }{2}T1+x^Tc_2x+\frac{\tau }{2}P1\right) \ge 0\\ & \qquad \Rightarrow (2T1+2P1+Mx)\tau ^2+4(x^Txc_1+x^Tc_2x)\tau -4x\le 0. \end{aligned}$$

Utilizing the auxiliary variables (6), a series of equations are obtained as follows:

$$\begin{aligned} B_i\tau ^2+C_i\tau +D_i\le 0,\quad i=1,2,\ldots ,k. \end{aligned}$$

(36)

(6) confirms that $C_i\ge 0$ and $D_i\le 0$. Thus, when $\tau$ satisfies (36) and $\tau >0$, there exist three situations.

• 1. when $B_i>0$,

  $$\begin{aligned} \tau =\frac{\sqrt{C_i^2-4B_iD_i}-C_i}{2B_i}. \end{aligned}$$

• 2. when $B_i=0$,

  $$\begin{aligned} \tau =-\frac{D_i}{C_i}. \end{aligned}$$

• 3. when $B_i<0$,

  $$\begin{aligned} \tau =\frac{\sqrt{C_i^2-4B_iD_i}-C_i}{2B_i}. \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \begin{aligned} \tau&=min \{\frac{\sqrt{C_i^2-4B_iD_i}-C_i}{2B_i},\quad when\; B_i\ne 0; \\ &\quad -\frac{D_i}{C_i},\; when\; B_i=0\},\; i=1,2,\ldots ,k. \\ \end{aligned} \end{aligned}$$

(37)

(37) guarantees (35) hold. Thus, the updating rule (19) guarantees all constraints hold.

Now it has been proved that (18) and (19) are gradient descent methods for (16). Therefore, (16) is non-increasing under (18) and (19).