Skip to main content

Advertisement

Springer Nature Link
Log in

Novel group decision-making method based on interval-valued m-polar fuzzy soft expert information

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

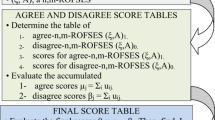
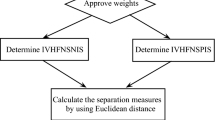
Abstract

In mathematical modeling and decision analysis, the multipolar uncertainty is prevalent and requires specialized approaches. The theory of m-polar fuzzy (mF, in short) set is a strong extension of the fuzzy set because of its feature for dealing with multi-polar information, and robust hybrid models such as mF soft sets and interval-valued mF soft sets have emerged for significant real-life multi-criteria decision-making applications. However, these models are limited when it comes to accommodating multiple decision-makers individually in some real situations that emphasize making the use of multi-polar, multi-agent, and multi-object approaches of uncertainty. For example, in the selection of a professor, different evaluation reports are considered from more than one expert. In contrast, the soft expert set model can deal with the opinions of multiple experts about available alternatives regarding multiple attributes but fails to accommodate interval-valued mF knowledge. Motivated by these facts, in this research study, we introduce the notion of an interval-valued mF soft expert set (IV\(_m\)FSE set) model, a multiple criteria group decision-making (MCGDM) approach, by integrating interval-valued m-polar fuzziness with soft expert sets. The initiated hybrid model is an expert extension of the IV\(_m\)F soft sets or an interval-valued extension of the mF soft expert sets. Moreover, we discuss properties of certain unary and binary operations and relations on IV\(_m\)FSE sets (the ‘AND’ operation, the ‘OR’ operation, subset-relation, equality, complement, agree- and disagree-IV\(_m\)FSE sets, union, and intersection) and illustrate these operations with numerical examples. Further, we implement the proposed theory in a group decision-making problem for the fabrication of upper limb prosthesis samples to visualize its importance and significance. We also design an algorithm to illustrate the procedure of the proposed method. Finally, to validate the aptitude and novelty of the proposed theory, we give its comparative analysis with some preexisting fuzzy theories, including mF soft expert sets and fuzzy soft expert sets, by applying them to a real-world problem in which nine upper limb prosthesis samples are considered, and the computed results depict that the optimal decision alternative is \(x_2\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

All data generated or analyzed during this study are included in this article.

References

  1. Adam F, Hassan N (2016) Multi \(Q\)-fuzzy soft expert set and its application. J Intell Fuzzy Syst 30(2):943–950

    MATH  Google Scholar 

  2. Akram M (2019) \(m\)-Polar fuzzy graphs, Studies in Fuzziness and Soft Computing, vol 371. Springer, Berlin

    Google Scholar 

  3. Akram M, Ali G, Butt MA, Alcantud JCR (2021) Novel MCGDM analysis under \(m\)-polar fuzzy soft expert sets. Neural Comput Appl 33:12051–12071

    Google Scholar 

  4. Akram M, Ali G, Alcantud JCR, Fatimah F (2021) Parameter reduction analysis under interval-valued \(m\)-polar fuzzy soft information. Artif Intell Rev 54:5541–5582

    Google Scholar 

  5. Akram M, Siddique S, Alcantud JCR (2023) Connectivity indices of \(m\)-polar fuzzy network model, with an application to a product manufacturing problem. Artif Intell Rev 56:7795-7838

    Google Scholar 

  6. Akram M, Sultan M, Alcantud JCR (2023) An integrated ELECTRE method for selection of rehabilitation center with \(m\)-polar fuzzy \(N\)-soft information. Artif Intell Med 135:102449

    Google Scholar 

  7. Alcantud JCR, Feng F, Yager RR (2020) An \(N\)-soft set approach to rough sets. IEEE Trans Fuzzy Syst 28(11):2996–3007

    Google Scholar 

  8. Ali G, Akram M (2020) Decision-making method based on fuzzy \(N\)-soft expert sets. Arab J Sci Eng 45:10381–10400

    Google Scholar 

  9. Ali G, Akram M, Shahzadi S, Abidin MZU (2021) Group decision-making framework with bipolar soft expert sets. J Multiple-Valued Logic Soft Comput 37(3–4):211–246

    MathSciNet  MATH  Google Scholar 

  10. Ali G, Afzal M, Asif M, Shazad A (2022) Attribute reduction approaches under interval-valued \(q\)-rung orthopair fuzzy soft framework. Appl Intell 52(8):8975–9000

    Google Scholar 

  11. Ali G, Akram M (2022) Group decision-making analysis under interval-valued \(q\)-rung orthopair fuzzy soft expert sets. In: Real life applications of multiple criteria decision making techniques in fuzzy domain, pp 163–194, Springer Nature Singapore, Singapore

  12. Ali MI, Feng F, Liu XY, Min WK, Shabir M (2009) On some new operations in soft set theory. Comput Math Appl 57(9):1547–1553

    MathSciNet  MATH  Google Scholar 

  13. Alkhazaleh S, Salleh AR (2011) Soft expert sets. Adv Decis Sci 2011:12. https://doi.org/10.1155/2011/757868

    Article  MathSciNet  MATH  Google Scholar 

  14. Alkhazaleh S, Salleh AR (2014) Fuzzy soft expert set and its application. Appl Math 5(09):1349–1368

    Google Scholar 

  15. Al-Qudah Y, Hassan N (2017) Bipolar fuzzy soft expert set and its application in decision making. Int J Appl Decis Sci 10(2):175–191

    Google Scholar 

  16. Arockiarani I, ArokiaLancy AA (2013) Multi criteria decision making problem with soft expert set. International journal of Computer Applications 78(15):1–4

    Google Scholar 

  17. Aydin T, Engino\(\breve{\rm {g}}\)lu S (2021) Interval-valued intuitionistic fuzzy parameterized interval-valued intuitionistic fuzzy soft sets and their application in decision-making. J Ambient Intell Humaniz Comput 12(1):1541–1558

  18. Bashir M, Salleh AR (2021) Fuzzy parameterized soft expert set. Abstr Appl Anal. https://doi.org/10.1155/2012/258361

    Article  MATH  Google Scholar 

  19. Bera S, Pal M (2022) A novel concept of domination in m-polar interval-valued fuzzy graph and its application. Neural Comput Appl 34(1):745–756

    Google Scholar 

  20. Bin C (2020) Interval valued generalised fuzzy soft expert set and its application. In: Liu Y, Wang L, Zhao L, Yu Z (eds) Advances in natural computation, fuzzy systems and knowledge discovery. ICNC-FSKD 2019. Advances in intelligent systems and computing, vol 1074. Springer, Cham. https://doi.org/10.1007/978-3-030-32456-8_106

    Chapter  Google Scholar 

  21. Broumi S, Smarandache F (2015) Intuitionistic fuzzy soft expert sets and its application in decision making. J New Theory 1:89–105

    Google Scholar 

  22. Chen J, Li S, Ma S, Wang X (2014) \(m\)-polar fuzzy sets: an extension of bipolar fuzzy sets. Sci World J 2014:8

    Google Scholar 

  23. Das AK, Granados C (2022) Interval-valued fuzzy parameterized multi fuzzy N-soft set in decision-making. In: Mukherjee S, Muppalaneni NB, Bhattacharya S, Pradhan AK (eds) Intelligent systems for social good advanced technologies and societal change. Springer, Singapore. https://doi.org/10.1007/978-981-19-0770-8_11

    Chapter  Google Scholar 

  24. Das N, Nagpal N, Bankura SS (2018) A review on the advancements in the field of upper limb prosthesis. J Med Eng Technol 42(7):532–545

    Google Scholar 

  25. Deschrijver G, Kerre EF (2003) On the relationship between some extensions of fuzzy set theory. Fuzzy Sets Syst 133(2):227–235

    MathSciNet  MATH  Google Scholar 

  26. Fatimah F, Alcantud JCR (2021) The multi-fuzzy N-soft set and its applications to decision-making. Neural Comput Appl 33:11437–11446

    Google Scholar 

  27. Feng F, Li Y, Fotea VL (2010) Application of level soft sets in decision-making based on interval-valued fuzzy soft sets. Comput Math Appl 60:1756–1767

    MathSciNet  MATH  Google Scholar 

  28. Garg H (2021) New exponential operation laws and operators for interval-valued \(q\)-rung orthopair fuzzy sets in group decision making process. Neural Comput Appl 33:13937–13963

    Google Scholar 

  29. Gorzalczany MB (1987) A method of inference in approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets Syst 21(1):1–17

    MathSciNet  MATH  Google Scholar 

  30. Greenfield S, Chiclana F, Dick S (2016) Interval-valued complex fuzzy logic. In: 2016 IEEE international conference on fuzzy systems (FUZZ-IEEE), IEEE, pp. 2014–2019

  31. Han Y, Deng Y, Cao Z, Lin CT (2020) An interval-valued Pythagorean prioritized operator-based game theoretical framework with its applications in multicriteria group decision making. Neural Comput Appl 32(12):7641–7659

    Google Scholar 

  32. Hassan N, Alhazaymeh K (2013) Vague soft expert set theory. In: AIP conference proceedings, vol 1522(1), pp 953–958

  33. Huang J, Li Z, Xia H, Chen G, Meng Q (2023) Cross-modal integration and transfer learning using fuzzy logic techniques for intelligent upper limb prosthesis. IEEE Trans Fuzzy Syst 31(4):1267–1280

    Google Scholar 

  34. Igual C, Pardo LA Jr, Hahne JM, Igual J (2019) Myoelectric control for upper limb prostheses. Electronics 8(11):1244

    Google Scholar 

  35. Jan N, Gwak J, Choi J, Lee SW, Kim CS (2023) Transportation strategy decision-making process using interval-valued complex fuzzy soft information. AIMS Math 8(2):3606–3633

    Google Scholar 

  36. Joshi BP, Singh A, Bhatt PK, Vaisla KS (2018) Interval valued \(q\)-rung orthopair fuzzy sets and their properties. J Intell Fuzzy Syst 35(5):5225–5230

    Google Scholar 

  37. Jiang Y, Tang Y, Chen Q, Liu H, Tang J (2010) Interval-valued intuitionistic fuzzy soft sets and their properties. Comput Math Appl 60(3):906–918

    MathSciNet  MATH  Google Scholar 

  38. Jiang Y, Tang Y, Chen Q (2011) An adjustable approach to intuitionistic fuzzy soft sets based decision-making. Appl Math Model 35:824–836

    MathSciNet  MATH  Google Scholar 

  39. Mahapatra T, Sahoo S, Ghorai G, Pal M (2021) Interval valued m-polar fuzzy planar graph and its application. Artif Intell Rev 54:1649–1675

    Google Scholar 

  40. Mahapatra T, Ghorai G, Pal M (2022) Competition graphs under interval-valued \(m\)-polar fuzzy environment and its application. Comput Appl Math 41(6):1–35

    MathSciNet  MATH  Google Scholar 

  41. Mahapatra T, Pal M (2022) An investigation on \(m\)-polar fuzzy tolerance graph and its application. Neural Comput Appl 34(4):3007–3017

    Google Scholar 

  42. Mio R, Sanchez M, Valverde Q, Lara J, Rumiche F (2018) Mechanical testing methods for body-powered upper-limb prostheses: a case study. In: IEEE 18th international conference on bioinformatics and bioengineering https://doi.org/10.1109/BIBE.2018.00040

  43. Maji PK, Biswas R, Roy AR (2003) Soft set theory. Comput Math Appl 45(4–5):555–562

    MathSciNet  MATH  Google Scholar 

  44. Maji PK, Roy AR, Biswas R (2002) An application of soft sets in a decision-making problem. Comput Math Appl 44(8):1077–1083

    MathSciNet  MATH  Google Scholar 

  45. Maji PK, Biswas R, Roy AR (2001) Fuzzy soft sets. J Fuzzy Math 9(3):589–602

    MathSciNet  MATH  Google Scholar 

  46. Molodtsov D (1999) Soft set theory: first results. Comput Math Appl 37(4–5):19–31

    MathSciNet  MATH  Google Scholar 

  47. Palanikumar M, Arulmozhi K (2023) Novel possibility Pythagorean interval valued fuzzy soft set method for a decision making. TWMS J Appl Eng Math 13(1):327–340

    Google Scholar 

  48. Pawlak Z (1982) Rough sets. Int J Comput Inform Sci 11(5):145–172

    MATH  Google Scholar 

  49. Precup RE, Teban TA, Albu A, Borlea AB, Zamfirache IA, Petriu EM (2020) Evolving fuzzy models for prosthetic hand myoelectric-based control. IEEE Trans Instrum Meas 69(7):4625–4636

    Google Scholar 

  50. Qayyum A, Abdullah S, Aslam M (2016) Cubic soft expert sets and their application in decision making. J Intell Fuzzy Syst 31(3):1585–1596

    MATH  Google Scholar 

  51. Roy AR, Maji PK (2007) A fuzzy soft set theoretic approach to decision-making problems. J Comput Appl Math 203(2):412–418

    MATH  Google Scholar 

  52. Sarwar M (2023) Decision making model for design concept evaluation based on interval rough integrated cloud VIKOR. J Ambient Intell Humaniz Comput 14:3875–3897

    Google Scholar 

  53. Sarwar M, Akram M, Liu P (2021) An integrated rough ELECTRE II approach for risk evaluation and effects analysis in automatic manufacturing process. Artif Intell Rev 54(6):4449–4481

    Google Scholar 

  54. Sarwar M, Akram M, Ali U (2020) Double dominating energy of \(m\)-polar fuzzy graphs. J Intell Fuzzy Syst 38(2):1997–2008

    Google Scholar 

  55. Selvachandran G, Singh PK (2018) Interval-valued complex fuzzy soft set and its application. Int J Uncertain Quantif 8(2):101–117

    MathSciNet  MATH  Google Scholar 

  56. Scheiterer ES, Leyendecker S (2022) Fuzzy forward dynamics of distinct gait phases with a prosthetic foot. Comput Mech 70:501–513

    MATH  Google Scholar 

  57. Su J, Deng Y (2022) An interval method to measure the uncertainty of basic probability assignment. Soft Comput 26:6041–6050

    Google Scholar 

  58. Yang XB, Lin TY, Yang JY, Li Y, Yu D (2009) Combination of interval-valued fuzzy set and soft set. Comput Math Appl 58(3):521–527

    MathSciNet  MATH  Google Scholar 

  59. Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353

    MATH  Google Scholar 

  60. Zhou X, Chen Y (2023) Multi-attribute decision-making method based on bipolar N-soft expert set. J Ambient Intell Humaniz Comput 14:2617–2630

    Google Scholar 

  61. Zulqarnain RM, Siddique I, Iampan A, Baleanu D (2022) Aggregation operators for interval-valued Pythagorean fuzzy soft set with their application to solve multi-attribute group decision making problem. Comput Model Eng Sci 2:1–34

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Division of Science and Technology, Department of Mathematics, University of Education, Lahore, 54770, Pakistan

    Ghous Ali

  2. Department of Mathematics, Government College Women University, Sialkot, Pakistan

    Musavarah Sarwar

  3. Department of Mathematics, COMSATS University Islamabad, Lahore Campus, Lahore, Pakistan

    Muhammad Nabeel

Authors
  1. Ghous Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Musavarah Sarwar
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Muhammad Nabeel
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ghous Ali.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest regarding the publication of this article.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ali, G., Sarwar, M. & Nabeel, M. Novel group decision-making method based on interval-valued m-polar fuzzy soft expert information. Neural Comput & Applic 35, 22313–22340 (2023). https://doi.org/10.1007/s00521-023-08869-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-023-08869-3

Keywords