Projection neural networks with finite-time and fixed-time convergence for sparse signal reconstruction

Abstract

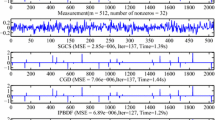
This paper considers the $L_1$-minimization problem for sparse signal and image reconstruction by using projection neural networks (PNNs). Firstly, a new finite-time converging projection neural network (FtPNN) is presented. Building upon FtPNN, a new fixed-time converging PNN (FxtPNN) is designed. Under the condition that the projection matrix satisfies the Restricted Isometry Property (RIP), the stability in the sense of Lyapunov and the finite-time convergence property of the proposed FtPNN are proved; then, it is proven that the proposed FxtPNN is stable and converges to the optimum solution regardless of the initial values in fixed time. Finally, simulation examples with signal and image reconstruction are carried out to show the effectiveness of our proposed two neural networks, namely FtPNN and FxtPNN.

Appendices

Appendix A

Proof of Theorem 1

The derivative of $V_1$ with respect to t is given as follows:

$$\begin{aligned} \dot{V_1}(\tilde{\textit{u}})=(P\tilde{b} + (I-P)\tilde{c})^T \dot{\tilde{\textit{u}}}, \end{aligned}$$

(23)

$\textit{u}^*$ is a constant, we can get

$$\begin{aligned} \dot{\tilde{\textit{u}}}=\dot{\textit{u}}= - \frac{{(I - P)g(\textit{u}) + Pw - q}}{{\left\| {(I - P)g(\textit{u}) + Pw - q} \right\| _2^{1 - \alpha }}}. \end{aligned}$$

(24)

As stated in the definition, FtPNN (11) has a equilibrium point $\textit{u}^*$, which indicates that

$$\begin{aligned}&-\lambda (\textit{u}^*)\phi (\textit{u}^*) = - \frac{{(I - 2P)g(\textit{u}^*) + P\textit{u}^* - q}}{{\left\| {(I - 2P) + g(\textit{u}^*)P\textit{u}^*- q} \right\| _2^{1 - \alpha }}} = 0 \nonumber \\&\Rightarrow \frac{{\phi (\textit{u}^*)}}{{\left\| {\phi (\textit{u}^*)} \right\| _2^{1 - \alpha }}} = 0\quad \textrm{or}\quad \lambda (\textit{u}^*)=0 \nonumber \\&\Rightarrow \frac{{\phi (\textit{u}^*)}}{{\left\| {\phi (\textit{u}^*)} \right\| _2^{1 - \alpha }}} = 0\quad \textrm{or}\quad \textit{u}^* \in Fin(\textit{u}) \nonumber \\&\Rightarrow \phi (\textit{u}^*)=0\quad \textrm{or}\quad \textit{u}^* \in Fin(\textit{u}), \end{aligned}$$

(25)

where $Fin(\textit{u}):= \{\textit{u} \in R^n: -Pu^* -(I - 2P)g(\textit{u}^*) + q = 0\}$.

Then, we can get it by inserting (24) into (23).

$$\begin{aligned} \dot{\tilde{\textit{u}}} = - \frac{{P\tilde{\textit{u}} + (I - 2P)\tilde{c}}}{{\left\| {P\tilde{\textit{u}} + (I - 2P)\tilde{c}} \right\| _2^{1 - \alpha }}} = 0. \end{aligned}$$

(26)

As a result of Eqs. (25) and (16), we can obtain

$$\begin{aligned} \dot{V_1}(\tilde{\textit{u}})&= -(P\tilde{b} + (I-P)\tilde{c})^T \frac{{P\tilde{\textit{u}} + (I - 2P)\tilde{c}}}{{\left\| {P\tilde{\textit{u}} + (I - 2P)\tilde{c}} \right\| _2^{1 - \alpha }}} \nonumber \\&= -(P(\tilde{\textit{u}}-\tilde{c}) + (I-P)\tilde{c})^T \frac{{P\tilde{\textit{u}} + (I - 2P)\tilde{c}}}{{\left\| {P\tilde{\textit{u}} + (I - 2P)\tilde{c}} \right\| _2^{1 - \alpha }}} \nonumber \\&= -{P\tilde{\textit{u}} + (I - 2P)\tilde{c}}^T \frac{{P\tilde{\textit{u}} + (I - 2P)\tilde{c}}}{{\left\| {P\tilde{\textit{u}} + (I - 2P)\tilde{c}} \right\| _2^{1 - \alpha }}} \nonumber \\&= -\frac{{\left\| {P\tilde{\textit{u}} + (I - 2P)\tilde{c}} \right\| _{2}^{2}}}{{\left\| {P\tilde{\textit{u}} + (I - 2P)\tilde{c}} \right\| _2^{1 - \alpha }}} \nonumber \\&= - {\left\| {P\tilde{\textit{u}} + (I - 2P)\tilde{c}} \right\| _2^{1 + \alpha }} \nonumber \\&\le 0. \end{aligned}$$

(27)

The value of $G(\tilde{\textit{u}})$ is now discussed. According to Eq. (7), we can acquire that the function $g(\cdot )$ is non-decreasing. For $\tilde{\textit{u}}_i \ge 0, {z_{1i}}(s)=g(s + \textit{u}_i^*) - g(\textit{u}_i^*)$, hence we can deduce that $\forall s \le 0, {z_{1i}}(s) \ge 0$, and consequently

$$\begin{aligned} G_i(\tilde{\textit{u}}_i) \ge 0. \end{aligned}$$

Further,

$$\begin{aligned} g(\textbf{x}) - g(\textbf{e}) \le \textbf{x} - \textbf{e},\quad \forall \textbf{x} \ge \textbf{e}, \end{aligned}$$

therefore,

$$\begin{aligned} G_i(\tilde{\textit{u}}_i) = {\int\limits _0^{\widetilde{\textit{u}}_i} {{z_{1i}}(s)ds = \int\limits _0^{\widetilde{\textit{u}}_i} {sds} = \frac{\widetilde{\textit{u}}_i^2}{2}}}. \end{aligned}$$

For $\tilde{\textit{u}}_i \ge 0, {z_{2i}}(s)=g(\textit{u}_i^*) - g(s + \textit{u}_i^*)$, hence we can deduce that $\forall s \le 0, {z_{2i}}(s) \ge 0$, and consequently

$$\begin{aligned} G_i(\tilde{\textit{u}}_i) \ge 0. \end{aligned}$$

Correspondingly, when $\forall s \le 0, {z_{2i}}(s) \le -s$,

$$\begin{aligned} g(\textbf{x}) - g(\textbf{e}) \le \textbf{x} - \textbf{e},\quad \forall \textbf{x} \ge \textbf{e}. \end{aligned}$$

As a result, the following conclusion can be drawn:

$$\begin{aligned} G_i(\tilde{\textit{u}}_i) = {\int\limits _{\widetilde{\textit{u}}_i}^{0} {{z_{2i}}(s)ds = \int\limits _{\widetilde{\textit{u}}_i}^0 {-sds} = \frac{\widetilde{\textit{u}}_i^2}{2}}}. \end{aligned}$$

The following is a summary of the above findings:

$$\begin{aligned} 0 \le G_i(\tilde{\textit{u}}_i) \le \frac{\widetilde{\textit{u}}_i^2}{2},\ \forall \tilde{\textit{u}}_i. \end{aligned}$$

(28)

Using Eq. (14) and (28), it is not difficult to obtain that

$$\begin{aligned} V_1(\tilde{\textit{u}})&=\textbf{1}^{T}PH(\tilde{\textit{u}}) + \textbf{1}^{T}(1-P)G(\tilde{\textit{u}})\\&\le \frac{1}{2}\delta _{\max }(P) \Vert \tilde{\textit{u}}\Vert _2^2 + \frac{1}{2}\delta _{\max }(I-P) \Vert \tilde{\textit{u}}\Vert _2^2. \end{aligned}$$

It is said that P is nonnegative (positive), and the matrix $(I-P)$ is a positive semi-definite matrix. The maximum eigenvalue is specified as $\delta _{\max }(\cdot )$. Define $\gamma$ such as:

$$\begin{aligned} \gamma = \frac{1}{2} \delta _{\max }(P) + \frac{1}{2} \delta _{\max }(I-P). \end{aligned}$$

One obtains

$$\begin{aligned} V_1(\tilde{\textit{u}}) \le \gamma \Vert \tilde{\textit{u}}\Vert _2^2, \end{aligned}$$

(29)

with $\gamma > 0$. It follows from Eq. (28) that

$$\begin{aligned} V_1(\tilde{\textit{u}}) = \textbf{1}^{T}PH(\tilde{\textit{u}}) + \textbf{1}^{T}(I-P)G(\tilde{\textit{u}}) \ge 0. \end{aligned}$$

(30)

Deduce $V_1$, then let be a radically unbounded Lyapunov function that is positive semi-definite based on (23) and (30). We can conclude that the FtPNN (11) is Lyapunov stable based on (27) and (30). According to the LaSalle invariance principle [42], we currently recognize that $\tilde{\textit{u}}$ will converge to an invariant subset of $M \triangleq \, \{\tilde{\textit{u}}\ \, \vert P\tilde{b} + (I-P)\tilde{c} = 0\}$ called $U_{inv}$. It is clear from (26) and (27) that $\dot{V}_1 = 0$ implies $\dot{\tilde{\textit{u}}} = 0$, hence all states of U are invariant. As a consequence, $U_{inv} = U$. Certainly, we can get $\textit{u}$ to converge to U, and then $g(\textit{u})$ to converge to a collection of optimal solutions (2). Theorem 1 has also been proven.

Proof of Theorem 2

Firstly, the relation of $\tilde{\textit{u}}$ and $\tilde{c}$ will be proved. Under the condition 2 of Lemma 3, $\textit{u}_i(t)$ will have the same sign as $\textit{u}^*$, after a finite time $t_1 < \infty$. We will consider the following two cases, respectively. (1): if $\vert \textit{u}^*_i(t)\vert < 1$, we can get $\vert \tilde{c}_i \vert =\vert g(\tilde{\textit{u}}_i+\textit{u}^*_i)-g(\textit{u}^*_i)\vert \le \vert \tilde{\textit{u}}_i \vert$. (2): if $\vert \textit{u}^*_i(t)\vert > 1$, we can get $\tilde{c}_i=g(\textit{u}_i)-g(\textit{u}^*_i) = g(\tilde{\textit{u}}_i+\textit{u}^*_i)-g(\textit{u}^*_i)$. Based on the condition 2 of Lemma 3, the presented FtPNN is globally convergent. It indicates that $\vert \tilde{\textit{u}}_i \vert$ is tiny, for any small $\mathfrak {p} > 0$, there is $t(\omega ) < \infty$, such that $\vert \tilde{\textit{u}}_i(t)\vert < \ell , \forall t>t(\ell )$. Then, $t>t_2$, define $t_2 = t(1-\mathfrak {p})$, we can get $\vert \tilde{\textit{u}}_i(t)\vert < 1-\mathfrak {p}$ that $\textit{u}^*_i$ and $\tilde{\textit{u}}_i + \textit{u}^*_i$ have the same sign, $\tilde{c}_i = 0$ obtained.

According to Assumption 1, P is an idempotent matrix that is also symmetric, we have $P^2=P, P\tilde{\textit{u}} = P^T P\tilde{\textit{u}}=\tilde{\textit{u}}$, then $P\tilde{c}=\tilde{c}$. Consequently,

$$\begin{aligned} \Vert P\tilde{\textit{u}} + (I-2P)\tilde{c}\Vert ^2_2 = \Vert \tilde{\textit{u}} + \tilde{c}-2\tilde{c}\Vert ^2_2 = \Vert \tilde{\textit{u}} -\tilde{c}\Vert ^2_2 \ge \Vert \tilde{\textit{u}}\Vert ^2_2 -\Vert \tilde{c}\Vert ^2_2. \end{aligned}$$

In the sequel, there exists a $t_e=\max \{t_1,t_2\}<\infty$, such that $\forall t, t>t_e$. We have, if $\vert \tilde{\textit{u}}_i^*\vert <1$, $\vert \tilde{c}_i\vert \le \vert \tilde{\textit{u}}_i\vert$, else if $\vert \tilde{\textit{u}}_i^*\vert >1$, $\tilde{c}_i = 0$. For simplicity, if $\vert \tilde{\textit{u}}_i^*\vert <1$, we denote $i \in \Gamma _c$, if $\vert \tilde{\textit{u}}_i^* \vert >1$, we denote $i \in \Gamma _b$. Therefore, $\Vert \tilde{c}\Vert \le \Vert \tilde{\textit{u}}\Vert = \Vert \tilde{\textit{u}_{\Gamma _b}}\Vert +\Vert \tilde{\textit{u}_{\Gamma _c}}\Vert$, then $\Vert \tilde{c}\Vert \le \Vert \tilde{\textit{u}_{\Gamma _b}}\Vert$.

Utilizing Assumption 1, $P_{\Gamma _b}$ and $P_{\Gamma _c}$ is not singular, thus $\Vert P\tilde{\textit{u}} + (I-2P)\tilde{c}\Vert ^2_2 > 0$ so long as $\Vert \tilde{\textit{u}}\Vert ^2_2>0$. Then, there is a small value $\chi$ such that $\Vert \tilde{c}\Vert \le \chi \Vert \tilde{\textit{u}}\Vert$, then

$$\begin{aligned} \Vert P\tilde{\textit{u}} + (I-2P)\tilde{c}\Vert ^2_2 \ge (1-\chi )\Vert \tilde{\textit{u}}\Vert ^2_2, \end{aligned}$$

(31)

where $(1-\chi ) >0$.

Next, the FtPNN (11) are considered, according to Eqs. (27) and (31), for $t>t_e$, we have

$$\begin{aligned} \dot{V_1}(\tilde{\textit{u}})= - {\left\| {P\tilde{\textit{u}} + (I - 2P)\tilde{c}} \right\| _2^{1 + \alpha }} \le -(1-\chi )^{(1+\alpha )/2}\Vert \tilde{\textit{u}}\Vert ^{(1 + \alpha )/2}_2. \end{aligned}$$

(32)

For all $t>t_e$, $V_1(\tilde{\textit{u}})$ converges to zero in finite time, and $t_f>t_e$. At last, one obtains $\forall t>t_f, \textit{u}=\textit{u}^*$.

From (A7) and (A10), one obtains,

$$\begin{aligned} \dot{V_1}(\tilde{\textit{u}}(t)) \le -(1-\chi )^{\frac{1+\alpha }{2}}\gamma ^{-\frac{1+\alpha }{4}} V_1(\tilde{\textit{u}}(t))^{\frac{1+\alpha }{4}}. \end{aligned}$$

(33)

In view of the above,

$$\begin{aligned}&V_1(\tilde{\textit{u}}(t))^{1-\frac{1+\alpha }{4}} - V_1(\tilde{\textit{u}}(0))^{1-\frac{1+\alpha }{4}}\nonumber \\&\quad =\int \limits^t_0\left( 1-\frac{1+\alpha }{4}\right) V_1(\tilde{\textit{u}}(t))^ {-\frac{1+\alpha }{4}}\dot{V_1}(\tilde{\textit{u}}(t))\textrm{d}t\nonumber \\&\quad \le -(1-\chi )^{\frac{1+\alpha }{2}}\gamma ^{-\frac{1+\alpha }{4}} \int\limits ^t_0\left( 1-\frac{1+\alpha }{4}\right) \textrm{d}t\nonumber \\&\quad =-(1-\chi )^{\frac{1+\alpha }{2}} \gamma ^{-\frac{1+\alpha }{4}}\left( 1-\frac{1+\alpha }{4}\right) t. \end{aligned}$$

(34)

Therefore, one observes that,

$$\begin{aligned} t \le \frac{4}{(3-\alpha )(1-\chi )^{\frac{1+\alpha }{2}} \gamma ^{-\frac{1+\alpha }{4}}}V_1(\tilde{\textit{u}}(0))^{\frac{3-\alpha }{4}}. \end{aligned}$$

(35)

Thus, we can get the FtPNN (11) can converge within $\frac{4}{(3-\alpha )(1-\chi )^{\frac{1+\alpha }{2}} \gamma ^{-\frac{1+\alpha }{4}}}V_1(\tilde{\textit{u}}(0))^{\frac{3-\alpha }{4}}$. Theorem 2 is proved. $\square$

Appendix B

Proof of Lemma 4

Consider the following matrix $H(\tilde{\textit{u}}_i(t))$. According to $\varrho (\cdot )$, it is possible to have

$$\begin{aligned} \varrho (\textbf{x})-\varrho (\textbf{e}) \le \textbf{x}-\textbf{e}, \quad \textrm{for} \quad \forall \textbf{x} \ge \textbf{e}, \end{aligned}$$

as a result,

$$\begin{aligned} \vert \tilde{c}_i(t)\vert = \vert \tilde{\alpha }_i(\tilde{\textit{u}}_i(t))\vert \le \vert \tilde{\textit{u}}_i(t)\vert , \quad \forall \tilde{\textit{u}}_i(t), \end{aligned}$$

(36)

we know that the function $\varrho (\cdot )$ is non-decreasing and $\alpha _i(s) = \varrho (s+\tilde{\textit{u}}_i^*)+\varrho (\tilde{\textit{u}}_i^*)$, and it indicates that $\tilde{\textit{u}}_i(t) \cdot \alpha _i(\tilde{\textit{u}}_i(t)) \ge 0$.

If $\tilde{\textit{u}}_i(t) \le 0, \alpha _i(\tilde{\textit{u}}_i(t)) \le 0$ and $\tilde{\textit{u}}_i(t) \le \alpha _i(\tilde{\textit{u}}_i(t))$, one obtains

$$\begin{aligned} H_i(\tilde{\textit{u}}_i(t)) = \int\limits _0^{\widetilde{\textit{u}}_i(t)} {{\beta _{i}}(s)ds} = \int \limits_{\widetilde{\textit{u}}_i(t)}^{0} {{\beta _{i}}(s)ds} = \int\limits _0^{\widetilde{\textit{u}}_i(t)} {(-{\beta _{i}}(s)ds)}ds \le \int \limits_0^{\widetilde{\textit{u}}_i(t)}{-s}ds, \end{aligned}$$

therefore,

$$\begin{aligned} 0 \le H_i(\tilde{\textit{u}}_i(t)) \le \frac{\tilde{\textit{u}}_i^2(t)}{2}. \end{aligned}$$

Similarly, if $\tilde{\textit{u}}_i(t) \ge 0, \alpha _i(\tilde{\textit{u}}_i(t)) \ge 0$ and $\tilde{\textit{u}}_i(t) \ge \alpha _i(\tilde{\textit{u}}_i(t))$, we have

$$\begin{aligned} H_i(\tilde{\textit{u}}_i(t)) = \int\limits _0^{\widetilde{\textit{u}}_i(t)} {{\beta _{i}}(s)ds} \le \int \limits_0^{\widetilde{\textit{u}}_i(t)} {s}ds. \end{aligned}$$

Consequently, we can obtain the following:

$$\begin{aligned} 0 \le H_i(\tilde{\textit{u}}_i(t)) \le \frac{\tilde{\textit{u}}_i^2(t)}{2}. \end{aligned}$$

Therefore, we have $0 \le H_i(\tilde{\textit{u}}_i(t)) \le ((\tilde{\textit{u}}_i^2(t))/(2))$, for any $\tilde{\textit{u}}_i(t)$.

As shown in the previous demonstration, the same property on $G(\tilde{\textit{u}}(t))$ holds, which means that the conclusion holds.

Proof of Lemma 5

Consider the boundary of $\vert H_i(\tilde{\textit{u}}_j(t))\vert$. When $i \ne j$, one obtains

$$\begin{aligned} \vert H_i(\tilde{\textit{u}}_j(t))\vert&= \vert \int \limits_{\bar{\textit{u}}_j}^{\widetilde{\textit{u}}_j(t)} {\alpha _{i}(\rho _{ij}(s))}ds \vert \nonumber \\&\le \int \limits_{\bar{\textit{u}}_j}^{\widetilde{\textit{u}}_j(t)} {\vert \alpha _{i}(\rho _{ij}(s))\vert }ds \nonumber \\&= \int \limits_{\bar{\textit{u}}_j}^{\widetilde{\textit{u}}_j(t)} {\vert \varrho (\rho _{ij}(s)+\textit{u}_i^*)-\varrho (\textit{u}_i^*)\vert }ds \nonumber \\&= \int\limits _{\bar{\textit{u}}_j}^{\widetilde{\textit{u}}_j(t)} {\vert \tilde{c}_i(\rho _{ij}(s))\vert }ds. \end{aligned}$$

(37)

Furthermore, according to the condition 2 of Lemma 3, $\tilde{\textit{u}}(t)$, $\tilde{c}(t)$, and $\tilde{b}(t)$ are bounded, there are three constants $\tau _1$, $\tau _2$, and $\tau _3$ that make the following inequations established for each $\rho _{ij}(s)$ before the FxtMPNN (17) converges, i.e., $\Vert \tilde{\textit{u}}\Vert _2$:

$$\begin{aligned} \vert \tilde{c}_i(\rho _{ij}(s))\vert \le \tau _1 \Vert \tilde{\textit{u}}\Vert _2\\ \vert \tilde{\textit{u}}_j(t)-\bar{\textit{u}}_j\vert \le \tau _2 \Vert \tilde{\textit{u}}\Vert _2\\ \vert \tilde{b}_i(\rho _{ij}(s))\vert \le \tau _3 \Vert \tilde{\textit{u}}\Vert _2, \end{aligned}$$

where $\tau _1 > 0$, $\tau _2 > 0$, and $\tau _3 > 0$.

In addition,

$$\begin{aligned} \int \limits_{\bar{\textit{u}}_j}^{\widetilde{\textit{u}}_j(t)} {\vert \tilde{c}_i(\rho _{ij}(s))\vert }ds&\le \tau _1 \Vert \tilde{\textit{u}}\Vert _2 \int\limits _{\bar{\textit{u}}_j}^{\widetilde{\textit{u}}_j(t)} {}ds\\&= \tau _1 \Vert \tilde{\textit{u}}\Vert _2 \vert \tilde{\textit{u}}_j(t)-\bar{\textit{u}}_j\vert \\&\le \tau _1 \tau _2 \Vert \tilde{\textit{u}}\Vert _2^2, \end{aligned}$$

therefore,

$$\begin{aligned} \vert H_i(\tilde{\textit{u}}_j(t))\vert \le \tau _1 \tau _2 \Vert \tilde{\textit{u}}\Vert _2^2. \end{aligned}$$

According to Lemma 4, one obtains

$$\begin{aligned} H_i(\tilde{\textit{u}}_j(t)) \le \frac{1}{2} \tilde{\textit{u}}_2^2 \le \frac{1}{2} \Vert \tilde{\textit{u}}\Vert _2^2. \end{aligned}$$

Let $\tau ^{'}=\max \{\tau _1 \tau _2, 1/2\}$, we have

$$\begin{aligned} \vert H_i(\tilde{\textit{u}}_j(t))\vert \le \tau ^{'} \Vert \tilde{\textit{u}}\Vert _2^2, \quad \forall i,j, \end{aligned}$$

one obtains,

$$\begin{aligned} \vert Tr\{PH\}\vert&= \vert Tr\{P^{T}PH\}\vert = \left| \sum _{i=1}^N \sum _{j=1}^N \{P_i^{T}P_{j}H_i(\widetilde{\textit{u}}_j(t))\}\right| \nonumber \\&\le \sum _{i=1}^N \sum _{j=1}^N \vert P_i^{T}P_{j}\vert \cdot \vert H_i(\widetilde{\textit{u}}_j(t))\vert \nonumber \\&\le (\zeta \tau ^{'}(N^2-N)+ \tau ^{'}N)\Vert \tilde{\textit{u}}\Vert _2^2, \end{aligned}$$

(38)

where $\zeta$ is defined in (56).

Correspondingly, the following conclusion is reached based on the preceding discussion:

$$\begin{aligned} \vert G_i(\tilde{\textit{u}}_j(t))\vert \le \tau ^{''} \Vert \tilde{\textit{u}}\Vert _2^2, \quad \forall i,j, \end{aligned}$$

where $\tau ^{''}=\max \{\tau _2 \tau _3, 1/2\}$, one obtains,

$$\begin{aligned} \vert Tr\{PH\}\vert \le (\zeta \tau ^{''}(N^2-N)+ \tau ^{''}N)\Vert \tilde{\textit{u}}\Vert _2^2. \end{aligned}$$

(39)

Using Lemma 4, one obtains,

$$\begin{aligned} 0 \le \vert Tr(G)\vert \le \sum _{i=1}^N{G_i(\tilde{\textit{u}}_i(t))} \le \frac{N}{2}\Vert \tilde{\textit{u}}_i(t)\Vert _2^2, \end{aligned}$$

(40)

it follows from (38) and (40) that

$$\begin{aligned} \vert V_2(\tilde{\textit{u}}_i(t))\vert&= \vert Tr\{PH(\tilde{\textit{u}}_i(t))\} + Tr\{(I-P)G(\tilde{\textit{u}}_i(t))\}\vert \nonumber \\&\le \vert Tr\{PH\}\vert + \vert Tr(G)\vert + \vert Tr(PG)\vert \nonumber \\&\le \vert Tr\{PH\}\vert + \frac{N}{2}\Vert \tilde{\textit{u}}_i(t)\Vert _2^2 + \vert Tr(PG)\vert \nonumber \\&\le ((\zeta \tau ^{'}(N^2-N)+\tau ^{'}N) + \frac{N}{2} + \tau ^{''}(N^2-N)+\tau ^{''}N)\Vert \tilde{\textit{u}}_i(t)\Vert _2^2. \end{aligned}$$

(41)

As a result, a positive constant $\psi$ exists, one obtains $V_2(\tilde{\textit{u}}(t)) \le \psi \Vert \tilde{\textit{u}}_i(t)\Vert _2^2$, where $\psi = (\zeta \tau ^{'}(N^2-N)+\tau ^{'}N) + \frac{N}{2} + \tau ^{''}(N^2-N)+\tau ^{''}N$. Since $\tau ^{'} \ge 1/2, \tau ^{''} \ge 1/2$, thus there exists $\psi \ge 3N/2$.

Proof of Lemma 6

According to the proof of Theorem 2, the FxtPNN is Lyapunov stable. $V_2$ is bounded, which is proved by Lemma 5. Hence, according to LaSalle theorem [42], the FxtPNN (17) converges to a invariant set L, where

$$\begin{aligned} L=\{\tilde{\textit{u}} \vert P\tilde{c}+(I-P)\tilde{b}=0\}. \end{aligned}$$

As we know, the solution of FxtPNN is unique. That is to say, the invariant set L has one unique element, i.e. $\tilde{\textit{u}}=0$ and $V_2(\tilde{\textit{u}})=0$. Accordingly, $\Vert P\tilde{c}+(I-P)\tilde{b}\Vert ^2_2 \ne 0$ and $\Vert \tilde{\textit{u}}\Vert ^2_2 \ne 0$ are tenable before the FxtPNN converges. Under this premise, there exists two constants $0<\kappa <1$ and o, such that

$$\begin{aligned} o \Vert \tilde{\textit{u}}\Vert ^2_2 \le \Vert P\tilde{c}+(I-P)\tilde{b}\Vert ^2_2, \end{aligned}$$

where

$$\begin{aligned} o = \left\{ \begin{array}{ll} \kappa \frac{\Vert P\tilde{c}+(I-P)\tilde{b}=0\Vert ^2_2}{\Vert \tilde{\textit{u}}\Vert ^2_2}, \quad &{}\textrm{if} \ \Vert P\tilde{c}+(I-P)\tilde{b}=0\Vert ^2_2 < \Vert \tilde{\textit{u}}\Vert ^2_2,\\ \kappa , \quad &{}\textrm{if} \ \Vert P\tilde{c}+(I-P)\tilde{b}=0\Vert ^2_2 \ge \Vert \tilde{\textit{u}}\Vert ^2_2, \end{array}\right. \end{aligned}$$

with $o \in (0,1)$.

Proof of Lemma 7

Since $\tilde{\textit{u}} = \textit{u}(t)-\textit{u}^*$, $\textit{u}^*$ is a constant, one obtains,

$$\begin{aligned} \dot{\tilde{\textit{u}}} = \dot{\textit{u}}&= -\frac{{P(w(t)) + (I - P)g(\textit{u}(t)) - q}}{{\left\| {P(w(t)) + (I - P)g(\textit{u}(t)) - q} \right\| _2^{1 - \alpha }}} - \frac{{P(w(t)) + (I - P)g(\textit{u}(t)) - q}}{{\left\| {P(w(t)) + (I - P)g(\textit{u}(t)) - q} \right\| _2^{1 - \beta }}} \nonumber \\&= -\frac{{P(c(t)) + (I - P)b(t) - q}}{{\left\| {P(c(t)) + (I - P)b(t) - q} \right\| _2^{1 - \alpha }}} - \frac{{P(c(t)) + (I - P)b(t) - q}}{{\left\| {P(c(t)) + (I - P)b(t) - q} \right\| _2^{1 - \beta }}}. \end{aligned}$$

(42)

From FxtPNN (17), $\textit{u}^*$ is the equilibrium point, one obtains,

$$\begin{aligned} -\eta (\textit{u}^*)\phi (\textit{u}^*)&= - \frac{{(I - 2P)g(\textit{u}^*) + P\textit{u}^* - q}}{{\left\| {(I - 2P) + g(\textit{u}^*)P\textit{u}^*- q} \right\| _2^{1 - \alpha }}} - \frac{{(I - 2P)g(\textit{u}^*) + P\textit{u}^* - q}}{{\left\| {(I - 2P) + g(\textit{u}^*)P\textit{u}^*- q} \right\| _2^{1 - \beta }}} = 0\nonumber \\&\Rightarrow \frac{{\phi (\textit{u}^*)}}{{\left\| {\phi (\textit{u}^*)} \right\| _2^{1 - \alpha }}}+ \frac{{\phi (\textit{u}^*)}}{{\left\| {\phi (\textit{u}^*)} \right\| _2^{1 - \beta }}}= 0\quad \textrm{or}\quad \lambda (\textit{u}^*)=0 \nonumber \\&\Rightarrow \frac{{\phi (\textit{u}^*)}}{{\left\| {\phi (\textit{u}^*)} \right\| _2^{1 - \alpha }}} + \frac{{\phi (\textit{u}^*)}}{{\left\| {\phi (\textit{u}^*)} \right\| _2^{1 - \alpha }}} = 0\quad \textrm{or}\quad \textit{u}^* \in Fin(\textit{u}) \nonumber \\&\Rightarrow \phi (\textit{u}^*)=0\quad \textrm{or}\quad \textit{u}^* \in Fin(\textit{u}), \end{aligned}$$

(43)

we can get $c^*$ and $b^*$ are the equilibrium points, such that,

$$\begin{aligned} q = Pc^* + (I - P)b^*, \end{aligned}$$

(44)

then, combing (42) and (44), one obtains

$$\begin{aligned} \dot{\tilde{\textit{u}}}&= -\frac{{P(c - c^*) + (I - P)(b-b^*)}}{{\left\| {P(c - c^*) + (I - P)(b-b^*)} \right\| _2^{1 - \alpha }}} - \frac{{P(c - c^*) + (I - P)(b-b^*)}}{{\left\| {P(c - c^*) + (I - P)(b-b^*)} \right\| _2^{1 - \beta }}} \nonumber \\&= -\frac{{P\tilde{c} + (I - P)\tilde{b}}}{{\left\| {P\tilde{c} + (I - P)\tilde{b}} \right\| _2^{1 - \alpha }}} - \frac{{P\tilde{c} + (I - P)\tilde{b}}}{{\left\| {P\tilde{c} + (I - P)\tilde{b}} \right\| _2^{1 - \beta }}}. \end{aligned}$$

(45)

We have a derivation rule based on the changeable upper limit of the integral, therefore

$$\begin{aligned} \frac{dH_i(\tilde{\textit{u}}_j(t))}{dt}&= \frac{dH_i(\tilde{\textit{u}}_j(t))}{\tilde{\textit{u}}_j}\frac{d\tilde{\textit{u}}_j}{dt} = \frac{d \int_c^{\tilde{\textit{u}}_j(t)} {\alpha _i(\rho _{ij}(s))ds}}{d\tilde{\textit{u}}_j} = \alpha _i(\rho _{ij}(\tilde{\textit{u}}_j)) \dot{\tilde{\textit{u}}}_j=\tilde{c}_i \dot{\tilde{\textit{u}}}_j, \end{aligned}$$

(46)

and

$$\begin{aligned} \frac{dG_i(\tilde{\textit{u}}_j(t))}{dt}&= \frac{dG_i(\tilde{\textit{u}}_j(t))}{\tilde{\textit{u}}_j}\frac{d\tilde{\textit{u}}_j}{dt} = \frac{d \int_c^{\tilde{\textit{u}}_j(t)} {\beta _i(\rho _{ij}(s))ds}}{d\tilde{\textit{u}}_j} = \beta _i(\rho _{ij}(\tilde{\textit{u}}_j)) \dot{\tilde{\textit{u}}}_j=\tilde{b}_i \dot{\tilde{\textit{u}}}_j. \end{aligned}$$

(47)

Therefore,

$$\begin{aligned} \frac{dTr(PH(\tilde{\textit{u}}))}{dt} = \frac{d\sum _{i=1}^{N} \sum _{j=1}^{N} p_i^T p_j H_i(\tilde{\textit{u}}_j(t))}{dt} = \sum _{i=1}^{N} \sum _{j=1}^{N} p_i^T p_j \tilde{c}_i \dot{\tilde{\textit{u}}}_j = (P\tilde{c})^T \dot{\tilde{\textit{u}}}(t), \end{aligned}$$

(48)

and

$$\begin{aligned} \frac{dTr\{(I-P)G(\tilde{\textit{u}})\}}{dt}&= \frac{d\sum _{i=1}^{N} G_i(\tilde{\textit{u}}_i(t))}{dt} - \frac{d\sum _{i=1}^{N} \sum _{j=1}^{N} p_i^T p_j G_i(\tilde{\textit{u}}_j(t))}{dt} \nonumber \\&= \sum _{i=1}^{N} \tilde{b}_i \dot{\tilde{\textit{u}}}_j(t) - \sum _{i=1}^{N} \sum _{j=1}^{N} p_i^T p_j \tilde{b}_i \dot{\tilde{\textit{u}}}_j = ((I-P)\tilde{b})^T \dot{\tilde{\textit{u}}}(t). \end{aligned}$$

(49)

Thus, by (20), we get

$$\begin{aligned} \dot{V}_2&= \frac{dV^T}{d\tilde{\textit{u}}} \frac{d\tilde{\textit{u}}}{dt} = (P\tilde{c} + (I - P)\tilde{b})^T \dot{\tilde{\textit{u}}}(t) \nonumber \\&= (P\tilde{c} + (I - P)\tilde{b})^T\left[-\frac{{P\tilde{c} + (I - P)\tilde{b}}}{{\left\| {P\tilde{c}(t) + (I - P)\tilde{b}} \right\| _2^{1 - \alpha }}} - \frac{{P\tilde{c} + (I - P)\tilde{b}}}{{\left\| {P\tilde{c} + (I - P)\tilde{b}} \right\| _2^{1 - \beta }}}\right] \nonumber \\&= -\left\| {P\tilde{c} + (I - P)\tilde{b}} \right\| _2^{1 + \alpha } - \left\| {P\tilde{c} + (I - P)\tilde{b}} \right\| _2^{1 + \beta }, \end{aligned}$$

(50)

we get $\dot{V}_2 \le 0$.

Proof of Theorem 3

With respect to Lemma 5, one obtains,

$$\begin{aligned} V_2(\tilde{\textit{u}}) \le \psi \Vert \tilde{\textit{u}}\Vert _2^2, \end{aligned}$$

and, form Lemma 4, we have

$$\begin{aligned} \xi \Vert \tilde{\textit{u}}\Vert _2^2 \le \Vert P\tilde{c} + (I - P)\tilde{b}\Vert _2^2, \end{aligned}$$

so that we can obtain

$$\begin{aligned} \Vert P\tilde{c} + (I - P)\tilde{b}\Vert _2^2 \ge \frac{\xi }{\psi } V_2(\tilde{\textit{u}}). \end{aligned}$$

(51)

By Eq. (51), we get

$$\begin{aligned}&\Vert P\tilde{c} + (I - P)\tilde{b}\Vert _2^{1+\alpha } \ge \left( \frac{\xi V_2(\tilde{\textit{u}})}{\psi }\right) ^{(1+\alpha )/2} \nonumber \\&\Vert P\tilde{c} + (I - P)\tilde{b}\Vert _2^{1+\beta } \ge \left( \frac{\xi V_2(\tilde{\textit{u}})}{\psi }\right) ^{(1+\beta )/2}. \end{aligned}$$

(52)

From Eqs. (50) and (52),

$$\begin{aligned} \dot{V_2}(\tilde{\textit{u}})&= (P\tilde{c} + (I - P)\tilde{b})^T \left[ -\frac{{P\tilde{c} + (I - P)\tilde{b}}}{{\left\| {P\tilde{c} + (I - P)\tilde{b}} \right\| _2^{1 - \alpha }}} - \frac{{P\tilde{c} + (I - P) \tilde{b}}}{{\left\| {P\tilde{c} + (I - P)\tilde{b}} \right\| _2^{1 - \beta }}}\right] \nonumber \\&= - \left\| {P\tilde{c} + (I - P)\tilde{b}} \right\| _2^{1 + \alpha } - \left\| {P\tilde{c} + (I - P)\tilde{b}} \right\| _2^{1 + \beta } \nonumber \\&\le -(\frac{\xi V_2(\tilde{\textit{u}})}{\psi })^{(1+\alpha )/2} - \left( \frac{\xi V_2(\tilde{\textit{u}})}{\psi }\right) ^{(1+\beta )/2}= - \left( \frac{\xi V_2(\tilde{\textit{u}})}{\psi }\right) ^{1+(\alpha +\beta )/2}. \end{aligned}$$

(53)

Based on Lemmas 6 and 2, the following conclusion can be drawn. The settling time $\mathcal {T}$ satisfies:

$$\begin{aligned} \mathcal {T} \le \mathcal {T}_{\max } = \frac{2\left( \frac{\xi }{\psi }\right) ^{-(1+\alpha )/2}}{1-\alpha } + \frac{2\left( \frac{\xi }{\psi }\right) ^{-(1+\beta )/2}}{\beta -1}. \end{aligned}$$

(54)

Using Lemma 3, for all $t \ge \mathcal {T}$ and random initial conditions, $V_2=0$.

And from (B31), one obtains,

$$\begin{aligned} \dot{V_2}(\tilde{\textit{u}}(t)) \le -\left( \frac{\xi }{\psi }\right) ^{(1+\alpha )/2} V_2(\tilde{\textit{u}}(t))^{(1+\alpha )/2} - \left( \frac{\xi }{\psi }\right) ^{(1+\beta )/2}V_2(\tilde{\textit{u}}(t))^{(1+\beta )/2}. \end{aligned}$$

(55)

Define a positive constant $t_1$ to prove fixed-time convergence, and $V_2(\tilde{\textit{u}}(t_1))=1$. This leads to

$$\begin{aligned}&V_2(\tilde{\textit{u}}(t))^{1-(1+\alpha )/2}+ V_2(\tilde{\textit{u}}(t_1))^{1-(1+\beta )/2}-V_2(\tilde{\textit{u}} (t_1))^{1-(1+\alpha )/2}-V_2(\tilde{\textit{u}}(0))^{1-(1+\beta )/2}\nonumber \\ &\quad= \int\limits _{t_1}^{\mathcal {T}}\left( \frac{1-\alpha }{2}\right) V_2(\tilde{\textit{u}} (t))^{-(1+\alpha )/2}\dot{V}_2(\tilde{\textit{u}}(t))dt+\int \limits_0^{t_1} \left( \frac{1-\alpha }{2}\right) V_2(\tilde{\textit{u}}(t))^{-(1+\beta )/2} \dot{V}_2(\tilde{\textit{u}}(t))dt \nonumber \\ &\quad\le-\,\left( \frac{\xi }{\psi }\right) ^{(1+\alpha )/2} \int \limits^{\mathcal {T}}_{t_1} \frac{1-\alpha }{2}dt-\left( \frac{\xi }{\psi }\right) ^{(1+\beta )/2} \int \limits^{t_1}_{0} \frac{1-\beta }{2}dt \nonumber \\ &\quad =-\,\left( \frac{\xi }{\psi }\right) ^{(1+\alpha )/2} \frac{1-\alpha }{2}({\mathcal {T}}-t_1)-\left(\frac{\xi }{\psi }\right)^{(1+\beta )/2} \frac{1-\beta }{2} t_1. \end{aligned}$$

(56)

And then, the converge time can be obtained as follows:

$$\begin{aligned} {\mathcal {T}}-t_1 \le \left( \frac{\psi }{\xi }\right) ^{\frac{1+\alpha }{2}}\frac{2}{(1-\alpha )}, \end{aligned}$$

(57)

that is,

$$\begin{aligned} {\mathcal {T}}\le \left( \frac{\psi }{\xi }\right) ^{\frac{1+\alpha }{2}}\frac{2}{(1-\alpha )}+t_1. \end{aligned}$$

(58)

Meanwhile,

$$\begin{aligned} -\left( \frac{\xi }{\psi }\right) ^{\frac{1+\beta }{2}}\frac{(1-\beta )}{2} t_1=1-V_2(\tilde{\textit{u}}(0))^{\frac{(1-\beta )}{2}}\le 1, \end{aligned}$$

(59)

then,

$$\begin{aligned} t_1\le \frac{2}{(\beta -1)}\left( \frac{\psi }{\xi }\right) ^{\frac{1+\beta }{2}}. \end{aligned}$$

(60)

Substituting (60) into (58) yields the converge time,

$$\begin{aligned} {\mathcal {T}}\le \left( \frac{\psi }{\xi }\right) ^{\frac{1+\alpha }{2}}\frac{2}{(1-\alpha )}+\frac{2}{(\beta -1)}\left( \frac{\psi }{\xi }\right) ^{\frac{1+\beta }{2}}. \end{aligned}$$

(61)