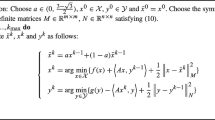Skip to main content
SpringerLink
Log in

A projected decentralized variance-reduction algorithm for constrained optimization problems

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

Solving constrained optimization problems that require processing large-scale data is of significant value in practical applications, and such problems can be described as the minimization of a finite-sum of local convex functions. Many existing works addressing constrained optimization problems have achieved a linear convergence rate to the exact optimal solution if the constant step-size was sufficiently small. However, they still suffer from low computational efficiency because of the computation of the local batch gradients at each iteration. Considering high computational efficiency to resolve the constrained optimization problems, we introduce the projection operator and variance-reduction technique to propose a novel projected decentralized variance-reduction algorithm, namely P-DVR, to tackle the constrained optimization problem subject to a closed convex set. Theoretical analysis shows that if the local function is strongly convex and smooth, the P-DVR algorithm can converge to the exact optimal solution at a linear convergence rate \({\mathcal {O}} ( {\hat{\lambda }}^{k} )\) with a sufficiently small step-size, where \(0< {\hat{\lambda }} < 1\). Finally, we experimentally validate the effectiveness of the algorithm, i.e., the algorithm possesses high computational efficiency and exact convergence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Abbreviations

x :

A vector in \(\mathbb {R}^p\)

\(\Vert \cdot \Vert\) :

The 2-norm of a vector

\(\preceq\) :

The less-than-equal symbol for comparing the size of each element of two vectors or two matrices

\(\succeq\) :

The greater-than-equal symbol for comparing the size of each element of two vectors or two matrices

\(\Omega\) :

The closed convex set contained in \(\mathbb {R}^{m \times p}\)

\(\Omega _{0}\) :

The closed convex set contained in \(\mathbb {R}^{p}\)

\(P_{\Omega }\) :

Projection operator for a closed convex set \(\Omega\)

\(P_{\Omega _{0}}\) :

Projection operator for a closed convex set \(\Omega _{0}\)

\(x_{k}^{i}\) :

Parameters of the k-th iteration of the i-th node in \(\mathbb {R}^{p}\)

\(x_{k}\) :

All parameters of the k-th iteration of the network in \(\mathbb {R}^{m \times p}\)

\(\bar{x}_{k}\) :

Average parameters of \(x_{k}^{i}\), \(i = 1, \ldots , m\), and \(\bar{x}_{k} \in \mathbb {R}^{p}\)

\(s_{k}^{i}\) :

The output of the projection operator \(P_{\Omega _{0}}\) when the input is \(x_{k}^{i}\), and \(s_{k}^{i} \in \mathbb {R}^{p}\)

\(s_{k}\) :

The output of the projection operator \(P_{\Omega }\) when the input is \(x_{k}\), and \(s_{k} \in \mathbb {R}^{m \times p}\)

\(\bar{s}_{k}\) :

Average parameters of \(s_{k}^{i}\), \(i = 1, \ldots , m\), and \(\bar{s}_{k} \in \mathbb {R}^{p}\)

\(y_{k}^{i}\) :

Auxiliary variables for the k-th gradient tracking of the i-th node in \(\mathbb {R}^{p}\)

\(y_{k}\) :

All auxiliary variables for the k-th gradient tracking in \(\mathbb {R}^{m \times p}\)

\(\bar{y}_{k}\) :

Average parameters of \(y_{k}^{i}\), \(i = 1, \ldots , m\), and \(\bar{y}_{k} \in \mathbb {R}^{p}\)

\(g_{k}^{i}\) :

Auxiliary variables for the k-th stochastic gradient of the i-th node, also noted as \(g ( s_{k}^{i} ) \in \mathbb {R}^{p}\)

\(g_{k}\) :

All auxiliary variables for the k-th stochastic gradient, also noted as \(g ( s_{k} ) \in \mathbb {R}^{m \times p}\)

f :

The global function of the optimization problem mapping from \(\mathbb {R}^p\) to \(\mathbb {R}\)

\(f^{i}\) :

The local function of the optimization problem mapping from \(\mathbb {R}^p\) to \(\mathbb {R}\)

\(f^{i,j}\) :

The local component function of the optimization problem mapping from \(\mathbb {R}^p\) to \(\mathbb {R}\)

\(\nabla f^{i}(x)\) :

The gradient of the local function f at \(x = x^{i} \in \mathbb {R}^{p}\)

\(\nabla F(x)\) :

The concatenation of the gradients of all local functions at \(x = [x^{1}, \ldots , x^{m}]^{\rm{T}} \in \mathbb {R}^{m \times p}\)

\(I_{m}\) :

Identity matrix in \(\mathbb {R}^{m \times m}\)

A :

Matrix in \(\mathbb {R}^{m \times m}\)

\(\rho (A)\) :

The spectral radius of A

\(\mathcal {G}\) :

Undirected graph

\(\mathcal {V}\) :

The set of the nodes of the graph \(\mathcal {G}\)

\(\mathcal {E}\) :

The set of the edges of the graph \(\mathcal {G}\)

References

  1. Luan L, Qin S (2022) Neurodynamic algorithms for constrained distributed convex optimization over fixed or switching topology with time-varying communication delay. Neural Comput Appl. https://doi.org/10.1007/s00521-022-07399-8

    Article  Google Scholar 

  2. Blatt D, Hero AO (2006) Energy-based sensor network source localization via projection onto convex sets. IEEE Trans Signal Process 54(9):3614–3619

    Google Scholar 

  3. He X, Yu J, Huang T, Li C (2019) Distributed power management for dynamic economic dispatch in the multimicrogrids environ-ment. IEEE Trans Control Syst Technol 27(4):1651–1658

    Google Scholar 

  4. Maros M and Jalden J (2019) ECO-PANDA: A computationally economic, geometrically converging dual optimization method on time-varying undirected graphs, Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, United Kingdom , May 2019, pp. 5257-5261

  5. Wen X, Wang Y, Qin S (2021) A nonautonomous-differential-inclusion neurodynamic approach for nonsmooth distributed optimization on multi-agent systems. Neural Comput Appl 33(20):13909–13920

    Google Scholar 

  6. Tsitsiklis J, Bertsekas D, Athans M (1986) Distributed asynchronous deterministic and stochastic gradient optimization algorithms. IEEE Trans Autom Control 31(9):803–812

    MathSciNet  Google Scholar 

  7. Li Y, Zhang H, Huang B, Han J (2020) A distributed Newton-Raphson-based coordination algorithm for multi-agent optimization with discrete-time communication. Neural Comput Appl 32(9):4649–4663

    Google Scholar 

  8. Kar S, Moura JMF (2013) Consensus + innovations distributed inference over networks: cooperation and sensing in networked systems. IEEE Signal Process Mag 30(3):99–109

    Google Scholar 

  9. Zeng P, Cui S, Song C, WangZ Li G (2022) A multiagent deep deterministic policy gradient-based distributed protection method for distribution network. Neural Comput Appl. https://doi.org/10.1007/s00521-022-06982-3

    Article  Google Scholar 

  10. Nedic A (2020) Distributed gradient methods for convex machine learning problems in networks: distributed optimization. IEEE Signal Process Mag 37(3):92–101

    Google Scholar 

  11. Liu Q, Wang J (2015) A second-order multi-agent network for bound constrained distributed optimization. IEEE Trans Autom Control 60(12):3310–3315

    MathSciNet  Google Scholar 

  12. Shi G, Johansson KH, Hong Y (2013) Reaching an optimal consensus: dynamical systems that compute intersections of convex sets. IEEE Trans Autom Control 58(3):610–622

    MathSciNet  Google Scholar 

  13. Qiu Z, Yang S, Wang J (2016) Distributed constrained optimal consensus of multi-agent systems. Automatica 68:209–215

    MathSciNet  Google Scholar 

  14. Lin P and Ren W (2012) Distributed subgradient projection algorithm for multi-agent optimization with nonidentical constraints and switching topologies, 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, , pp. 6813-6818

  15. Lin P, Ren W, Farrell JA (2017) Distributed continuous-time optimization: nonuniform gradient gains, finite-time convergence, and convex constraint set. IEEE Trans Autom Control 62(5):2239–2253

    MathSciNet  Google Scholar 

  16. Yan Z, Wang J, Li G (2014) A collective neurodynamic optimization approach to bound-constrained nonconvex optimization. Neural Netw 55:20–29

    Google Scholar 

  17. Huang Z, Liu F, Tang M, Qiu J, Peng Y (2020) A distributed computing framework based on lightweight variance reduction method to accelerate machine learning training on blockchain. China Commun 17(9):77–89

    Google Scholar 

  18. He L, Ye J, Jianwei E (2021) Accelerated proximal stochastic variance reduction for DC optimization. Neural Comput Appl 33(20):13163–13181

    Google Scholar 

  19. Xin R, Khan UA, Kar S (2020) Variance-reduced decentralized stochastic optimization with accelerated convergence. IEEE Trans Signal Process 68:6255–6271

    MathSciNet  Google Scholar 

  20. Defazio A, Bach F, Lacoste-Julien S (2014) SAGA: a fast incremental gradient method with support for non-strongly convex composite objectives. Adv Neural Inf Process Syst 27:1646–1654

    Google Scholar 

  21. De S, Goldstein T (2016) “Efficient distributed SGD with variance reduction," 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, pp. 111-120

  22. Shang-Guan S, Yin J (2017) A fast distributed principal component analysis with variance reduction, (2017) 16th International Symposium on Distributed Computing and Applications to Business, Engineering and Science (DCABES). Anyang, China 2017:11–14

  23. Zhang K, Liao X, Lü Q (2022) Privacy-protected decentralized dual averaging push with edge-based correlated perturbations over time-varying directed networks. IEEE Trans Netw Sci Eng 9(6):4145–4158

    MathSciNet  Google Scholar 

  24. Nedic A, Ozdaglar A, Parrilo PA (2010) Constrained consensus and optimization in multi-agent networks. IEEE Trans Autom Control 55(4):922–938

    MathSciNet  Google Scholar 

  25. Duchi JC, Agarwal A, Wainwright MJ (2012) Dual averaging for distributed optimization: convergence analysis and network scaling. IEEE Trans Autom Control 57(3):592–606

    MathSciNet  Google Scholar 

  26. Liu H, Yu W, Chen G (2022) Discrete-time algorithms for distributed constrained convex optimization with linear convergence rates. IEEE Trans Cybern 52(6):4874–4885

    Google Scholar 

  27. Nedic A, Ozdaglar A (2009) Distributed subgradient methods for multi-agent optimization. IEEE Trans Autom Control 54(1):48–61

    MathSciNet  Google Scholar 

  28. Sayin MO, Vanli ND, Kozat SS, Basar T (2017) Stochastic subgradient algorithms for strongly convex optimization over distributed networks. IEEE Trans Netw Sci Eng 4(4):248–260

    MathSciNet  Google Scholar 

  29. Li H, Lü Q, Chen G, Huang T, Dong Z (2021) Distributed constrained optimization over unbalanced directed networks using asynchronous broadcast-based algorithm. IEEE Trans Autom Control 66(3):1102–1115

    MathSciNet  Google Scholar 

  30. Wang Z, Wang D, Gu D (2020) Distributed optimal state consensus for multiple circuit systems with disturbance rejection. IEEE Trans Netw Sci Eng 7(4):2926–2939

    MathSciNet  Google Scholar 

  31. Loizou N, Rabbat M and Richtárik P(2019)“Provably accelerated randomized gossip algorithms," ICASSP 2019 - 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, pp. 7505-7509,

  32. Jakovetic D, Xavier J, Moura J (2014) Fast distributed gradient methods. IEEE Trans Autom Control 59(5):1131–1146

    MathSciNet  Google Scholar 

  33. Li H, Lü Q, Huang T (2019) Convergence analysis of a distributed optimization algorithm with a general unbalanced directed communication network. IEEE Trans Netw Sci Eng 6(3):237–248

    MathSciNet  Google Scholar 

  34. Nedic A, Olshevsky A, Shi W (2017) Achieving geometric convergence for distributed optimization over time-varying graphs. SIAM J Optim 27(4):2597–2633

    MathSciNet  Google Scholar 

  35. Qu G, Li N (2018) Harnessing smoothness to accelerate distributed optimization. IEEE Trans Control Netw Syst 5(3):1245–1260

    MathSciNet  Google Scholar 

  36. Xin R, Khan UA (2018) A linear algorithm for optimization over directed graphs with geometric convergence. IEEE Control Syst Lett 2(3):315–320

    MathSciNet  Google Scholar 

  37. Lü Q, Li H, Xia D (2018) Geometrical convergence rate for distributed optimization with time-varying directed graphs and uncoordinated step-sizes. Inf Sci 422:516–530

    MathSciNet  Google Scholar 

  38. Shi W, Ling Q, Wu G, Yin W (2015) EXTRA: an exact first-order algorithm for decentralized consensus optimization. SIAM J Optim 25(2):944–966

    MathSciNet  Google Scholar 

  39. Qureshi MI, Xin R, Kar S, Khan UA (2021) S-ADDOPT: decentralized stochastic first-order optimization over directed graphs. IEEE Control Syst Lett 5(3):953–958

    MathSciNet  Google Scholar 

  40. Pu S, Shi W, Xu J, Nedic A (2021) Push-pull gradient methods for distributed optimization in networks. IEEE Trans Autom Control 66(1):1–16

    MathSciNet  Google Scholar 

  41. Bin M, Notarnicola I, Marconi L and Notarstefano G (2019)“A system theoretical perspective to gradient-tracking algorithms for distributed quadratic optimization," Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, Dec. , pp. 2994-2999

  42. Scutari G, Sun Y (2019) Distributed nonconvex constrained optimization over time-varying digraphs. Math Program 176(1–2):497–544

    MathSciNet  Google Scholar 

  43. Yang S, Liu Q, Wang J (2018) A collaborative neurodynamic approach to multiple-objective distributed optimization. IEEE Trans Neural Netw Learn Syst 29(4):981–992

    Google Scholar 

  44. Stewart RH, Palmer TS, DuPont B (2021) A survey of multi-objective optimization methods and their applications for nuclear scientists and engineers. Prog Nucl Energy 138:103830

    Google Scholar 

  45. Pereira JLJ, Oliver GA, Francisco MB, Cunha SS, Gomes GF (2022) A review of multi-objective optimization: methods and algorithms in mechanical engineering problems. Arch Comput Method Eng 29(4):2285–2308

    Google Scholar 

  46. Andersson J (2000) “A survey of multiobjective optimization in engineering design,” Department of Mechanical Engineering, Linktjping University. Sweden

  47. Coello CAC (2007) Evolutionary algorithms for solving multi-Objective problems in Genetic and Evolutionary Computation Series. Springer, US

    Google Scholar 

  48. Zadeh L (1963) Optimality and non-scalar-valued performance criteria. IEEE Trans Autom Control 8(1):59–60

    Google Scholar 

  49. Xie P, You K, Tempo R, Song S, Wu C (2018) Distributed convex optimization with inequality constraints over time-varying unbalanced digraphs. IEEE Trans Autom Control 63(12):4331–4337

    MathSciNet  Google Scholar 

  50. Gao L, Deng S, Li H, Li C (2022) An event-triggered approach for gradient tracking in consensus-based distributed optimization. IEEE Trans Netw Sci Eng 9(2):510–523

    MathSciNet  Google Scholar 

  51. Zhang J, You K, Cai K (2020) Distributed dual gradient tracking for resource allocation in unbalanced networks. IEEE Trans Signal Process 68:2186–2198

    MathSciNet  Google Scholar 

  52. Horn RA, Johnson CR (2012) Matrix Anal. Cambridge University Press, Cambridge

    Google Scholar 

  53. Xiang Jim X (2013) A note on the cauchy-schwarz inequality. Amer Math Monthly 120(5):456–459

    MathSciNet  Google Scholar 

  54. Dua D and Graff C (2017) “UCI machine learning repository,"

  55. LeCun Y, Bottou L, Bengio Y, Haffner P (1998) Gradient-based learning applied to document recognition. Proc IEEE 86(11):2278–2324

    Google Scholar 

Download references

Acknowledgements

This work was supported in part by the Sichuan Key Laboratory of Smart Grid (Sichuan University) under grant 2023-IEPGKLSP-KFYB01, in part by the Natural Science Foundation of China under grants 62302068 and 62072061, in part by the Natural Science Foundation of Chongqing under grant CSTB2022NSCQ-MSX1627, in part by the China Postdoctoral Science Foundation under grant 2021M700588, in part by the project of Key Laboratory of Industrial Internet of Things & Networked Control, Ministry of Education under grant 2021FF09, in part by the Fundamental Research Funds for the Central Universities under grant 2023CDJXY-039, in part by the Chongqing Postdoctoral Science Foundation under grant 2021XM1006, in part by the National Key R&D Program of China under grant 2020YFB1805400 and 2022YFC3801700.

Author information

Authors and Affiliations

  1. College of Computer Science, Chongqing University, Chongqing, 400044, People’s Republic of China

    Shaojiang Deng, Shanfu Gao, Qingguo Lü & Yantao Li

  2. Key Laboratory of Smart Grid, Sichuan Province, Chengdu, 610065, People’s Republic of China

    Shaojiang Deng & Qingguo Lü

  3. College of Electronic and Information Engineering, Southwest University, Chongqing, 400715, People’s Republic of China

    Huaqing Li

Authors
  1. Shaojiang Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shanfu Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qingguo Lü
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yantao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Huaqing Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Qingguo Lü or Yantao Li.

Ethics declarations

Conflict of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data Availability Statement

The datasets generated and/or analyzed during the current study are available in the [UCI Machine Learning] repository, [https://archive.ics.uci.edu/ml/index.php].

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Deng, S., Gao, S., Lü, Q. et al. A projected decentralized variance-reduction algorithm for constrained optimization problems. Neural Comput & Applic 36, 913–928 (2024). https://doi.org/10.1007/s00521-023-09067-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-023-09067-x

Keywords

Search

Navigation