A new approach to multi-objective optimization of a tapered matrix distributed amplifier for UWB applications

Abstract

Using of ultra-wideband (UWB) technology in radio transceiver systems has increased in recent years due to high-speed data transmission, low power dissipation, low cost, and low complexity. In particular, distributed amplifier (DA) is a critical component of transceiver in UWB technology. However, designing an ultra-wideband DA with high performance becomes challenging. The DA design suffers from the tight trade-offs between the amplifier parameters such as gain, noise, linearity, input/output impedance matching, and power dissipation. In this paper, a new approach for multi-objective optimization of the DA is introduced. In the proposed approach, the meta-heuristic optimization techniques are applied over the entire bandwidth of the UWB, while the most recent optimization approaches for amplifiers are performed at the center frequency and they can’t achieve the proper design specifications for wideband amplifiers. The simultaneous optimization of power gain (S₂₁), noise figure (NF), input and output return loss (S₁₁ and S₂₂) are conducted over the wide bandwidth using three multi-objective optimization algorithms including Multi-Objective Inclined Planes System Optimization (MOIPO), Non-dominated Sorting Genetic Algorithm II (NSGA-II), and Multi-Objective Particle Swarm Optimization (MOPSO). The obtained results demonstrate the tapered matrix DA optimized by MOIPO exhibits better performance than others. The circuit simulations are performed in 0.18 µm TSMC RF-CMOS technology. Simulation results show that the optimized tapered matrix DA by MOIPO, compared to NSGA-II and MOPSO, exhibits a good performance over the frequency band of 0.1–28 GHz with maximum S₂₁ of 12.9 dB, NF less than 5.9 dB, S₁₁ and S₂₂ below than  − 10 dB over the whole frequency band. The DC power dissipation is 25 mW from a 1.5 V supply.

Appendices

Appendix 1

Figure 11 shows the structure of a conventional DA. As shown, the DA consists of two main sections, the gain cells and the gate and drain transmission lines. In CMOS technology, transmission lines are made by the LC network. In addition, the parasitic capacitors of the gain cell transistors (C_gs and C_gd) are usually used as the capacitors required for transmission lines. The input signal is applied to the gate transmission line, and each transistor receives a portion of the input signal and amplifies it through the transmission line. This generates a current at the drain terminal, which is identically divided to the left and right of the drain line. The power of the transistor amplified wave spreads directly in the direction of the load or reverses at any point of the drain line, which causes direct and reverse gain. To achieve a suitable gain, the currents of each transistor must be combined in parallel along the drain line to the amplifier output, meaning that the phase difference between the gate transmission line and the drain must be equal [31].

Fig. 11

The circuit of a conventional DA

By selecting the proper propagation constant and the length of the gate and drain transmission lines, the synchronous mode can be achieved. Impedance matching also absorbs waves that are propagating in the opposite direction. Due to the high losses in the gate transmission line, the cut-off frequency of this transmission line is usually lower than the drain line. Therefore, the gate transmission line capacitors (C_g) and its inductors (L_g) limit the cut-off frequency of DAs [32]. The gain of a conventional distributed amplifier is given as follows:

$$A_{{\text{V}}} = \frac{{nG_{{\text{m}}} \left( s \right)R_{{\text{L}}} }}{2}$$

(6)

where n and G_m are the number of stages and the transconductance of each stage, respectively, R_L is the load of the transmission line. To attain the maximum available power gain, it is essential that the characteristic impedance and the cut-off frequency of the gate transmission lines be equal. The cut-off frequency and characteristic impedance of gate and drain transmission lines are given as follows:

$$f_{{\text{g}}} = f_{{\text{d}}} = \frac{1}{{\pi \sqrt {L_{{\text{g}}} C_{{\text{g}}} } }} = \frac{1}{{\pi \sqrt {L_{{\text{g}}} C_{{\text{g}}} } }} = f_{{\text{c}}}$$

(7)

$$Z_{{\text{g}}} = Z_{{\text{d}}} = \sqrt {\frac{{L_{{\text{g}}} }}{{C_{{\text{g}}} }}} = \sqrt {\frac{{L_{{\text{d}}} }}{{C_{{\text{d}}} }}} = Z$$

(8)

According to (6), the gain of the amplifier is determined by the total transconductance and the number of parallel transistors. Also, the bandwidth of the amplifier is only limited by the cut-off frequency of parallel transistors. However, essentially, half of the output power is dissipated by the reverse currents that flew through one of the terminating resistors of the output transmission line. Therefore, with regards to the low power performance of DAs, their power consumption is fairly high. Moreover, adding any active and passive components leads to higher power dissipation and overall noise figure, as well. So far, various methodologies have been proposed to overcome these problems to some extent. Ginzton et al. [19] proposed a new DA by tapering the output transmission line, as shown in Fig. 12. According to (8), the smaller capacitance should be provided for higher value of the characteristic impedance at the output transmission line. Therefore, the size of the parallel transistors is reduced. Therefore, the tapered output transmission line limits the gain of the DA. Furthermore, the output impedance matching of the tapered DA is highly frequency-dependent as the terminating resistor on the left of the output transmission line has been removed.

Fig. 12

Schematic of DA with tapered output transmission line [19]

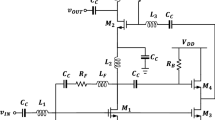
The matrix DA structure has been proposed to use multiplicative and additive gain mechanisms simultaneously [20]. The basic schematic of the matrix DA is illustrated in Fig. 13. Ideally, due to the reverse currents of interstage transmission line amplification, the matrix DAs exhibit higher gain than cascaded amplifiers. However, the power consumption of the matrix DA is relativity high due to terminating resistors at the output and interstage transmission lines. Moreover, the gain of the matrix DA is highly frequency-dependent because of multiple reverse amplification paths, which introduce different delays.

Fig. 13

The basic schematic of a 2 × N matrix DA

As illustrated in Fig. 14, using the new technique proposed in [22] for tapered DA, the coefficients of the gain cell’s current and characteristic impedance of the first section are a₀ = b₀ = 1.

Fig. 14

Schematic of a tapered output transmission line of an N-section tapered DA

The current coefficient of the gain cell and the characteristic impedance of the kth section is also given respectively as follows [22]:

$$a_{k} = \frac{{S - \mathop \sum \nolimits_{i = 0}^{k - 1} a_{i} }}{S}$$

(9)

$$b_{k} = \frac{1}{{a_{k} }}$$

(10)

where S denotes the sum of the current coefficients and is obtained as follows:

$$S = \mathop \sum \limits_{i = 0}^{N - 1} a_{i}$$

(11)

where N presents the number of parallel gain cells in the DA. In this design, S is assumed to be equal to 3. It should be noted Eq. (10) cannot be satisfied for the leftmost section (k = N−1), and the value for a_N−1 is given by [22]:

$$a_{N - 1} = S - \mathop \sum \limits_{i = 0}^{N - 2} a_{i}$$

(12)

$$b_{N - 1} = \frac{S}{{a_{N - 1} }}$$

(13)

Appendix 2

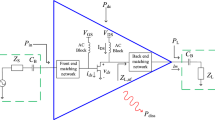
Today, the modern signal processing systems utilize a combination of analog and digital techniques, and are implemented on a chip, have three main goals of short design time, increasing productivity, and reducing circuit complexity. The semiconductor component manufacturing technologies have reached nanometer dimensions and are growing exponentially, but the computer-aided design (CAD) tools of analog circuits are not grown in this proportion. All kinds of meta-heuristic optimization algorithms seem to be suitable tools for analog RF circuit optimization. The purpose of optimization is to find the best acceptable solutions, given the constraints and needs of the problem. For a problem, there may be different solutions that are defined for comparing them and selecting the optimal solution called the objective function. For example, direct power gain (S₂₁), noise figure (NF) and input return loss (S₁₁), and output return loss (S₂₂) are the common objectives of the optimizing DA circuits. Sometimes simultaneous optimization is considered. Such optimization problems, which include multiple objective functions, are called multi-objective problems. In multi-objective optimization, the goal is to solve problems such as [15]:

$${\text{Minimize:}}\quad F\left( x \right) = \left[ {f_{1} \left( x \right), f_{2} \left( x \right), \ldots , f_{{\text{m}}} \left( x \right)} \right]$$

(14)

Subject to:

$$g_{i} \left( x \right) \le 0\quad i = 1, 2, \ldots , P$$

(15)

$$h_{j} \left( x \right) \le 0\quad j = 1, 2, \ldots , q$$

(16)

where x = [x₁, x₂,...,x_n]^T is the vector of decision variables, f_i: Rⁿ → R, i = 1,...,m are the objective functions and g_i, h_j: Rⁿ → R, i = 1,..., p, j = 1,..., q are the constraint functions of the problem. The target is to achieve a solution that works for (15) and (16).

Figure 15 shows the relationship between the MATLAB environment and the circuit simulator software. It should be noted the circuit simulation is carried out by Advanced Design System (ADS) with 180-nm RF-TSMC CMOS technology. First, the input information, including the size of the design parameters, is specified by MATLAB. Then, ADS is executed, and finally, the objective functions for processing are read.

Fig. 15

The structure of the optimization process