Skip to main content
Springer Nature Link
Log in

Identification of nonlinear dynamical system based on adaptive radial basis function neural networks

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

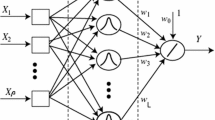
In this paper, an adaptive radial basis function neural network (RBFNN) is investigated and presented for identifying the nonlinear dynamical system. In traditional RBFNN structure, the selections of the activated radius are decided by the designer’s experience to satisfy the best approximation of nonlinear dynamical function. In order to reduce the experience error, an adaptive RBFNN mechanism that can realize auto-regulation of activated radius is proposed in this paper. Taking the lattice points as the center of activated function, we use Taylor expansion to separate the factor of activated radius in local space. In order to ensure that the identification error has the property of fast convergence, the error conversion function is used for shrinking the gain in the error differential equation. Constructing a Lyapunov function to determine the differential equation of the weights and the activated radius, it is shown that the weights and the activated radius will converge to the neighborhood of its true value and the identification error will converge to neighborhood of zero in a periodic or period-like nonlinear dynamical system. To illustrate the effectiveness of the proposed adaptive RBFNN, Vanderpol and Duffing dynamical system are used as test examples, in comparison with traditional RBFNN and wavelet neural networks (WNN). The results show that the proposed method has best accurate identification and approximating effect in all of test algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The data used to support the findings of this study are included within the article.

References

  1. Kumar R, Srivastava S, Gupta JRP, Mohindru A (2018) Diagonal recurrent neural network based identification of nonlinear dynamical systems with Lyapunov stability based adaptive learning rates. Neurocomputing 287:102–117

    Article  Google Scholar 

  2. Xu L, Ding F, Yang E (2020) Separable recursive gradient algorithm for dynamical systems based on the impulse response signals. Int J Control Autom Syst 18(12):3167–3177

    Article  Google Scholar 

  3. Denis V, Jossic M, Giraud-Audine C, Chomette B, Renault A, Thomas O (2018) Identification of nonlinear modes using phase-locked-loop experimental continuation and normal form. Mech Syst Signal Process 106:430–452

    Article  Google Scholar 

  4. Zhang S, Wang S, Jing F, Tan M (2019) A sensorless hand guiding scheme based on model identification and control for industrial robot. IEEE Trans Ind Inf 15(9):5204–5213

    Article  Google Scholar 

  5. Gupta V, Mittal M (2020) A novel method of cardiac arrhythmia detection in electrocardiogram signal. Int J Med Eng Inf 12(5):489–499

    Google Scholar 

  6. Deng M, Wang C, Zheng T (2018) Individual identification using a gait dynamics graph. Pattern Recogn 83:287–298

    Article  Google Scholar 

  7. Alexandridis A, Chondrodima E, Giannopoulos N, Sarimveis H (2016) A fast and efficient method for training categorical radial basis function networks. IEEE Trans Neural Netw Learn Syst 28(11):2831–2836

    Article  Google Scholar 

  8. Rahimilarki R, Gao Z, Zhang A, Binns R (2019) Robust neural network fault estimation approach for nonlinear dynamic systems with applications to wind turbine systems. IEEE Trans Ind Inf 15(12):6302–6312

    Article  Google Scholar 

  9. Fei J, Lu C (2017) Adaptive sliding mode control of dynamic systems using double loop recurrent neural network structure. IEEE Trans Neural Netw Learn Syst 29(4):1275–1286

    Article  Google Scholar 

  10. Puscasu G, Codres B, Stancu A, Murariu G (2009) Nonlinear system identification based on internal recurrent neural networks. Int J Neural Syst 19(02):115–125

    Article  Google Scholar 

  11. Pan Y, Wang J (2011) Model predictive control of unknown nonlinear dynamical systems based on recurrent neural networks. IEEE Trans Ind Electron 59(8):3089–3101

    Article  Google Scholar 

  12. Wu W, Wang C, Yuan C (2019) Deterministic learning from sampling data. Neurocomputing 358:456–466

    Article  Google Scholar 

  13. Kurdila AJ, Narcowich FJ, Ward JD (1995) Persistency of excitation in identification using radial basis function approximants. SIAM J Control Optim 33(2):625–642

    Article  MathSciNet  Google Scholar 

  14. Wang C, Hill DJ (2006) Learning from neural control. IEEE Trans Neural Netw 17(1):130–146

    Article  Google Scholar 

  15. Wang C, Hill DJ (2010) Deterministic learning and nonlinear observer design. Asian J Control 12(6):714–724

    Article  MathSciNet  Google Scholar 

  16. Sanner RM, Slotine J (1992) Gaussian networks for direct adaptive control. IEEE Trans Neural Netw 3(6):837–863

    Article  Google Scholar 

  17. Zheng T, Wang C (2017) Relationship between persistent excitation levels and RBF network structures, with application to performance analysis of deterministic learning. IEEE Trans Cybern 47(10):3380–3392

    Article  Google Scholar 

  18. Schilling RJ, Carroll JJ, Al-Ajlouni AF (2001) Approximation of nonlinear systems with radial basis function neural networks. IEEE Trans Neural Netw 12(1):1–15

    Article  Google Scholar 

  19. Luo G, Yang Z, Zhan C, Zhang Q (2021) Identification of nonlinear dynamical system based on raised-cosine radial basis function neural networks. Neural Process Lett 53(1):355–374

    Article  Google Scholar 

  20. Abiyev RH, Kaynak O (2008) Fuzzy wavelet neural networks for identification and control of dynamic plants-a novel structure and a comparative study. IEEE Trans Ind Electron 55(8):3133–3140

    Article  Google Scholar 

  21. Luo G, Yang Z, Zhang Q (2021) Identification of autonomous nonlinear dynamical system based on discrete-time multiscale wavelet neural network. Neural Comput Appl 33(22):15191–15203

    Article  Google Scholar 

  22. Zeng W, Yuan C (2021) ECG arrhythmia classification based on variational mode decomposition, Shannon energy envelope and deterministic learning. Int J Mach Learn Cybern 12(10):2963–2988

    Article  Google Scholar 

  23. Masood Z, Majeed K, Samar R, Raja MAZ (2017) Design of Mexican Hat Wavelet neural networks for solving Bratu type nonlinear systems. Neurocomputing 221:1–14

    Article  Google Scholar 

  24. Wirkus S, Rand R (2015) The dynamics of two coupled van der pol oscillators with delay coupling. Nonlinear Dyn 30(3):205–221

    Article  MathSciNet  Google Scholar 

  25. Zhang Q, Gao J, Dong H, Mao Y (2018) Wpd and de/bbo-rbfnn for solution of rolling bearing fault diagnosis. Neurocomputing 312(27):27–33

    Article  Google Scholar 

  26. Agarwal V, Zheng X, Balachandran B (2018) Influence of noise on frequency responses of softening Duffing oscillators. Phys Lett A 382(46):3355–3364

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to thank anonymous peer reviewer.

Author information

Authors and Affiliations

  1. School of Electrics and Computer Engineering, Nanfang College Guangzhou, Guangzhou, China

    Guo Luo, Hu Min & Zhi Yang

Authors
  1. Guo Luo
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hu Min
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zhi Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hu Min.

Ethics declarations

Conflict of interest

The authors (Guo Luo, Hu Min and Zhi Yang) declare that they have no conflict of financial or non-financial interests in relation to the work in this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luo, G., Min, H. & Yang, Z. Identification of nonlinear dynamical system based on adaptive radial basis function neural networks. Neural Comput & Applic 36, 15617–15629 (2024). https://doi.org/10.1007/s00521-024-09794-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-024-09794-9

Keywords