Skip to main content

Advertisement

Springer Nature Link
Log in

An integrated approach for prediction of magnitude using deep learning techniques

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

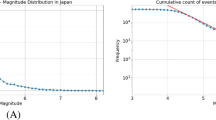
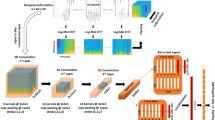
Abstract

Timely estimation of earthquake magnitude plays a crucial role in the early warning systems for earthquakes. Despite the inherent danger associated with earthquake energy, earthquake research necessitates extensive parameter estimation and predictive techniques to account for uncertain trends in earthquake waveforms when determining earthquake magnitudes using a single station. This study introduces an effective solution to tackle the issue through the automatic magnitude deep network (AMagDN) model. The proposed model includes long short-term memory (LSTM), a bidirectional LSTM, an autocorrelation attention mechanism, and a machine learning block that can capture detailed information from the seismic waveform recorded during an earthquake. The unique feature of this model is the use of multivariate time series waveforms derived from recorded accelerograms specifically tailored to their energy significance with magnitude and seven fusion tabular parameters involving source and geospatial features. The proposed model’s training, validation and testing are done using independent 15014, 1287 and 3448 records maintained by the Kyoshin network, Japan, for moderate to great impact earthquakes between 5.5 and 8.0 (\(M_\textrm{JMA}\)). A comparative study shows that the proposed model outperforms recent state-of-the-art models and common linear relations, reducing mean absolute prediction error by 40% from the second-best model. The multi-stations data are also used for successfully forecasting the magnitudes of two significant earthquakes of 7.7 and 7.3 magnitude (\(M_\textrm{JMA}\)) using the proposed model. The reliable prediction capabilities of the proposed model for both single and multi-station data clearly demonstrate its utility in reducing earthquake hazards.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Cofre A, Marin M, Pino OV, Galleguillos N, Riquelme S, Barrientos SE, Yoma NB (2022) End-to-end lstm-based earthquake magnitude estimation with a single station. IEEE Geosci Remote Sens Lett 19:1–5. https://doi.org/10.1109/LGRS.2022.3175108

    Article  Google Scholar 

  2. Cremen G, Galasso C (2020) Earthquake early warning: recent advances and perspectives. Earth Sci Rev 205:103184. https://doi.org/10.1016/j.earscirev.2020.103184

    Article  Google Scholar 

  3. Festa G, Picozzi M, Alessandro C, Colombelli S, Cattaneo M, Chiaraluce L, Elia L, Martino C, Marzorati S, Supino M, Zollo A (2017) Performance of earthquake early warning systems during the major events of the 2016–2017 central Italy seismic sequence. Seismol Res Lett. https://doi.org/10.1785/0220170150

    Article  Google Scholar 

  4. Berhich A, Belouadha FZ, Kabbaj MI (2023) An attention-based lstm network for large earthquake prediction. Soil Dyn Earthq Eng 165:107663. https://doi.org/10.1016/j.soildyn.2022.10766

    Article  Google Scholar 

  5. Wu Y, Zhao L (2006) Magnitude estimation using the first three seconds p-wave amplitude in earthquake early warning. Geophys Res Lett. https://doi.org/10.1029/2006GL026871

    Article  Google Scholar 

  6. Wu Y, Kanamori H (2005) Rapid assessment of damage potential of earthquakes in Taiwan from the beginning of p waves. Bull Seismol Soc Am 95:1181–1185. https://doi.org/10.1785/0120040193

    Article  Google Scholar 

  7. Wu Y, Kanamori H (2005) Experiment on an onsite early warning method for the Taiwan early warning system. Bull Seismol Soc Am 95:347–353. https://doi.org/10.1785/0120040097

    Article  Google Scholar 

  8. Wu Y, Yen H, Zhao L, Huang B, Liang W (2006) Magnitude determination using initial p waves: a single-station approach. Geophys Res Lett 33:05306. https://doi.org/10.1029/2005GL025395

    Article  Google Scholar 

  9. Kanamori H (2005) Real-time seismology and earthquake damage mitigation. Annu Rev Earth Planet Sci 33:195–214. https://doi.org/10.1146/annurev.earth.33.092203.122626

    Article  Google Scholar 

  10. Joshi A, Chalavadi V, Mohan K (2022) Early detection of earthquake magnitude based on stacked ensemble model. J Asian Earth Sci X 8:100122. https://doi.org/10.1016/j.jaesx.2022.100122

    Article  Google Scholar 

  11. Zhu J, Li S, Ma Q, He B, Song J (2022) Support vector machine-based rapid magnitude estimation using transfer learning for the sichuan-yunnan region, china. Bull Seismol Soc Am 112:894–904. https://doi.org/10.1785/0120210232

    Article  Google Scholar 

  12. Chanda S, Somala SN (2021) Single-component/single-station-based machine learning for estimating magnitude and location of an earthquake: A support vector machine approach. Pure Appl Geophys 178:1959–1976. https://doi.org/10.1007/s00024-021-02745-8

    Article  Google Scholar 

  13. Meng F, Ren T, Liu Z, Zhong Z (2023) Toward earthquake early warning: a convolutional neural network for repaid earthquake magnitude estimation. Artif Intell Geosci 4:39–46. https://doi.org/10.1016/j.aiig.2023.03.001

    Article  Google Scholar 

  14. Kong Q, Wang R, Walter WR, Pyle M, Koper KD, Schmandt B (2022) Combining deep learning with physics based features in explosion-earthquake discrimination. Geophys Res Lett. https://doi.org/10.1029/2022GL098645

    Article  Google Scholar 

  15. Banna MHA, Ghosh T, Nahian MJA, Taher KA, Kaiser MS, Mahmud M, Hossain MS, Andersson K (2021) Attention-based bi-directional long-short term memory network for earthquake prediction. IEEE Access 9:56589–56603. https://doi.org/10.1109/ACCESS.2021.3071400

    Article  Google Scholar 

  16. Bai T, Tahmasebi P (2021) Attention-based lstm-fcn for earthquake detection and location. Geophys J Int 228:1568–1576. https://doi.org/10.1093/gji/ggab401

    Article  Google Scholar 

  17. Wang Q, Guo Y, Yu L, Li P (2020) Earthquake prediction based on spatio-temporal data mining: an lstm network approach. IEEE Trans Emerg Top Comput 8:148–158. https://doi.org/10.1109/TETC.2017.2699169

    Article  Google Scholar 

  18. Wu H, Xu J, Wang J, Long M (2021) Autoformer: decomposition transformers with auto-correlation for long-term series forecasting. Neural Inf Process Syst 34:22419

    Google Scholar 

  19. Chen K, Zhou Y, Dai F (2015) A lstm-based method for stock returns prediction: a case study of china stock market. In: 2015 IEEE international conference on big data (big data), pp. 2823–2824. https://doi.org/10.1109/BigData.2015.7364089

  20. Xu K, Ba J, Kiros R, Cho K, Courville AC, Salakhutdinov R, Zemel RS, Bengio Y (2015) Show, attend and tell: neural image caption generation with visual attention. In: International conference on machine learning

  21. Wang Y, Huang M, Zhu X, Zhao L (2016) Attention-based lstm for aspect-level sentiment classification. In: Conference on empirical methods in natural language processing, pp. 606–615. https://doi.org/10.18653/v1/D16-1058

  22. Kardakis S, Perikos I, Grivokostopoulou F, Hatzilygeroudis I (2021) Examining attention mechanisms in deep learning models for sentiment analysis. Appl Sci 11:3883

    Article  Google Scholar 

  23. Bahdanau, D., Cho, K., Bengio, Y.: Neural machine translation by jointly learning to align and translate. arxiv: 1409.0473 (2014)

  24. Iaccarino AG, Guéguen P, Picozzi M, Ghimire S (2021) Earthquake early warning system for structural drift prediction using machine learning and linear regressors. Front Earth Sci 9:666444. https://doi.org/10.3389/feart.2021.666444

    Article  Google Scholar 

  25. Festa G, Zollo A, Lancieri M (2008) Earthquake magnitude estimation from early radiated energy. Geophys Res Lett 35:22307. https://doi.org/10.1029/2008GL035576

    Article  Google Scholar 

  26. Boatwright J, Fletcher JB (1984) The partition of radiated energy between p and s waves. Bull Seismol Soc Am 74:361–376. https://doi.org/10.1785/BSSA0740020361

    Article  Google Scholar 

  27. Mousavi SM, Beroza GC (2019) A machine-learning approach for earthquake magnitude estimation. Geophys Res Lett. https://doi.org/10.1029/2019GL085976

    Article  Google Scholar 

  28. Ristea N-C, Radoi A (2022) Complex neural networks for estimating epicentral distance, depth, and magnitude of seismic waves. IEEE Geosci Remote Sens Lett 19:1–5. https://doi.org/10.1109/LGRS.2021.3059422

    Article  Google Scholar 

  29. Perol T, Gharbi M, Denolle MA (2017) Convolutional neural network for earthquake detection and location. Sci Adv 4:1700578. https://doi.org/10.1126/sciadv.1700578

    Article  Google Scholar 

  30. Kundu A, Bhadauria YS, Basu S, Mukhopadhyay S (2017) Artificial neural network based estimation of moment magnitude with relevance to earthquake early warning. 2017 International conference on wireless communications, signal processing and networking (WiSPNET), 1955–1959. https://doi.org/10.1109/WiSPNET.2017.8300102

  31. Majstorović J, Giffard-Roisin S, Poli P (2021) Designing convolutional neural network pipeline for near-fault earthquake catalog extension using single-station waveforms. J Geophys Res Solid Earth. https://doi.org/10.1029/2020JB021566

    Article  Google Scholar 

  32. Ochoa LH, Niño LF, Vargas CA (2017) Fast magnitude determination using a single seismological station record implementing machine learning techniques. Geodesy Geodyn 9:34–41. https://doi.org/10.1016/j.geog.2017.03.010

    Article  Google Scholar 

  33. Wang C-Y, Huang T-C, Wu Y (2022) Using lstm neural networks for onsite earthquake early warning. Seismol Res Lett 93:814–826. https://doi.org/10.1785/0220210197

    Article  Google Scholar 

  34. Berhich A, Belouadha FZ, Kabbaj MI (2020) Lstm-based models for earthquake prediction. In: Proceedings of the 3rd international conference on networking, information systems security. 46: 1–7. https://doi.org/10.1145/3386723.3387865

  35. Apriani M, Wijaya SK (2021) Daryono: earthquake magnitude estimation based on machine learning: Application to earthquake early warning system. J Phys Conf Ser 1951:012057. https://doi.org/10.1088/1742-6596/1951/1/012057

    Article  Google Scholar 

  36. Wang Y, Li X, Wang Z, Liu J (2023) Deep learning for magnitude prediction in earthquake early warning. Gondwana Res 123:164–173. https://doi.org/10.1016/j.gr.2022.06.009

    Article  Google Scholar 

  37. Bilal MA, Wang Y, Ji Y, Akhter MP, Liu H (2023) Earthquake detection using stacked normalized recurrent neural network (snrnn). Appl Sci 13:8121. https://doi.org/10.3390/app13148121

    Article  Google Scholar 

  38. Allen RV (1978) Automatic earthquake recognition and timing from single traces. Bull Seismol Soc Am 68:1521–1532. https://doi.org/10.1785/BSSA0680051521

    Article  Google Scholar 

  39. Kang Q, Chen EJ, Li Z-C, Luo HB, Liu Y (2023) Attention-based lstm predictive model for the attitude and position of shield machine in tunneling. Underground Space 13:335–350. https://doi.org/10.1016/j.undsp.2023.05.006

    Article  Google Scholar 

  40. Xu Y, Liu T, Du P (2024) Volatility forecasting of crude oil futures based on bi-lstm-attention model: The dynamic role of the covid-19 pandemic and the russian-ukrainian conflict. Resour Policy 88:104319. https://doi.org/10.1016/j.resourpol.2023.104319

    Article  Google Scholar 

  41. Casolaro A, Capone V, Iannuzzo G, Camastra F (2023) Deep learning for time series forecasting: advances and open problems. Information 14:598. https://doi.org/10.3390/info14110598

    Article  Google Scholar 

  42. Joshi A, Chalavadi V, Mohan CK, Raman B (2023) Application of xgboost model for early prediction of earthquake magnitude from waveform data. J Earth Syst Sci. https://doi.org/10.1007/s12040-023-02210-1

    Article  Google Scholar 

  43. Zhu J, Li S, Song J (2022) Hybrid deep-learning network for rapid on-site peak ground velocity prediction. IEEE Trans Geosci Remote Sens 60:1–12. https://doi.org/10.1109/TGRS.2022.3230829

    Article  Google Scholar 

  44. Chatfield C (1981) The analysis of time series: an introduction. arXiv: Learning

  45. Papoulis A, Saunders H (1989) Probability, random variables and stochastic processes. arXiv: Learning

  46. Wiener N (1930) Generalized harmonic analysis. Acta Math 55:117–258. https://doi.org/10.1007/BF02546511

    Article  MathSciNet  Google Scholar 

  47. Hendrycks D, Gimpel, K (2016) Gaussian error linear units (gelus). arXiv: Learning

  48. Chen T, Guestrin C (2016) Xgboost: a scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. 785–794. https://doi.org/10.1145/2939672.2939785

  49. Breiman L (2001) Random forests. Mach Learn 45:5–32

    Article  Google Scholar 

  50. Ke G, Meng Q, Finley T, Wang T, Chen W, Ma W, Ye Q, Liu TY (2017) Lightgbm: a highly efficient gradient boosting decision tree. In: Proceedings of the 31st international conference on neural information processing systems, pp. 3149–3157

  51. Cortes C, Vapnik VN (1995) Support-vector networks. Mach Learn 20:273–297. https://doi.org/10.1007/BF00994018

    Article  Google Scholar 

  52. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Louppe G, Prettenhofer P, Weiss R, Weiss RJ, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E (2011) Scikit-learn: Machine learning in python. ArXiv abs/1201.0490

  53. Joshi A, Raman B, Mohan CK, Cenkeramaddi LR (2024) A new machine learning approach for estimating shear wave velocity profile using borelog data. Soil Dyn Earthq Eng 177:108424. https://doi.org/10.1016/j.soildyn.2023.108424

    Article  Google Scholar 

  54. Assaf JH, Molnar S, Naggar MHE (2023) Cpt-vs correlations for post-glacial sediments in metropolitan vancouver. Soil Dyn Earthq Eng 165:107693. https://doi.org/10.1016/j.soildyn.2022.107693

    Article  Google Scholar 

  55. Johnson R, Zhang T (2013) Accelerating stochastic gradient descent using predictive variance reduction. Adv Neural Inf Process Syst 26:315–323. https://doi.org/10.5555/2999611.2999647

    Article  Google Scholar 

  56. Aoi S, Kunugi T, Nakamura H, Fujiwara H (2011) Deployment of new strong motion seismographs of k-net and kik-net. Earthq Data Eng Seismol

  57. National Research Institute for Earth Science and Disaster Resilience (2019) NIED K-NET, KiK-net, National Research Institute for Earth Science and Disaster Resilience. https://doi.org/10.17598/NIED.0004

  58. Zare M, Bard P-Y (2002) Strong motion dataset of turkey: data processing and site classification. Soil Dyn Earthq Eng 22:703–718. https://doi.org/10.1016/S0267-7261(02)00028-3

    Article  Google Scholar 

  59. Mollova G (2007) Effects of digital filtering in data processing of seismic acceleration records. EURASIP J Adv Signal Process 2007:1–9. https://doi.org/10.1155/2007/29502

    Article  Google Scholar 

  60. Thompson MT (2006) Chapter 14: analog low-pass filters

  61. Rahman A, Marsono A, Rudyanto A (2017) Rapid magnitude estimation using \(\tau\)c method for earthquake early warning system (case study in sumatra). 1857: 020017. https://doi.org/10.1063/1.4987059

  62. Ikeda T, Tsuji T (2018) Temporal change in seismic velocity associated with an offshore mw 5.9 off-mie earthquake in the nankai subduction zone from ambient noise cross-correlation. Progr Earth Planet Sci 5:1–12. https://doi.org/10.1186/s40645-018-0211-8

    Article  Google Scholar 

  63. Shieh J-T, Wu Y, Allen RM (2008) A comparison of \(\tau\)c and \(\tau\)pmax for magnitude estimation in earthquake early warning. Geophys Res Lett. https://doi.org/10.1029/2008GL035611

    Article  Google Scholar 

  64. Zhu J, Li S, Song J, Wang Y (2021) Magnitude estimation for earthquake early warning using a deep convolutional neural network. Front Earth Sci. https://doi.org/10.3389/feart.2021.653226

    Article  Google Scholar 

  65. Nakamura Y (2003) A new concept for the earthquake vulnerability estimation and its application to the early warning system. In: Early warning systems for natural disaster reduction, pp. 693–699. https://doi.org/10.1007/978-3-642-55903-7_92

  66. Okamoto K, Tsuno S (2015) Investigation on relationship between epicentral distance and growth curve of initial p-wave propagating in local heterogeneous media for earthquake early warning system. Earth Planets Space 67:1–8. https://doi.org/10.1186/s40623-015-0339-3

    Article  Google Scholar 

  67. Kingma DP, Ba J (2014) Adam: A method for stochastic optimization. arxiv:abs/1412.6980

  68. Jin X, Zhang H, Li J, Wei Y, Ma Q (2013) Earthquake magnitude estimation using the \(\tau _c\) and \(p_d\) method for earthquake early warning systems. Earthq Sci 26:23–31. https://doi.org/10.1007/s11589-013-0005-4

    Article  Google Scholar 

  69. Scordilis E (2005) Globally valid relations converting ms, mb and mjma to mw, pp. 158–161

  70. Jain R, Nayyar A, Arora S, Gupta A (2021) A comprehensive analysis and prediction of earthquake magnitude based on position and depth parameters using machine and deep learning models. Multimedia Tools Appl 80:28419–28438. https://doi.org/10.1007/s11042-021-11001-z

    Article  Google Scholar 

Download references

Acknowledgement.

This study was funded by Prime Minister's Research Fellows (PMRF) under grand number PM-31-22-626-414.

Author information

Authors and Affiliations

  1. Department of Computer Science and Engineering, Indian Institute of Technology Roorkee, Roorkee, Uttarakhand, 247667, India

    Anushka Joshi & Balasubramanian Raman

  2. Department of Computer Science and Engineering, Indian Institute of Technology, Hyderabad, Sangareddy, Telangana, 502285, India

    C. Krishna Mohan

Authors
  1. Anushka Joshi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Balasubramanian Raman
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. C. Krishna Mohan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Anushka Joshi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Joshi, A., Raman, B. & Mohan, C.K. An integrated approach for prediction of magnitude using deep learning techniques. Neural Comput & Applic 36, 16991–17006 (2024). https://doi.org/10.1007/s00521-024-09891-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-024-09891-9

Keywords