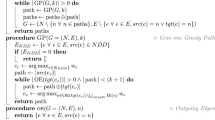Skip to main content
Springer Nature Link
Log in

Designing dataless neural networks for kidney exchange variants

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

Kidney transplantation is vital for treating end-stage renal disease, impacting roughly one in a thousand Europeans. The search for a suitable deceased donor often leads to prolonged and uncertain wait times, making living donor transplants a viable alternative. However, approximately 40% of living donors are incompatible with their intended recipients. Therefore, many countries have established kidney exchange programs, allowing patients with incompatible donors to participate in “swap” arrangements, exchanging donors with other patients in similar situations. Several variants of the vertex-disjoint cycle cover problem model the above problem, which deals with different aspects of kidney exchange as required. This paper discusses several specific vertex-disjoint cycle cover variants and deals with finding the exact solution. We employ the dataless neural networks framework to establish single differentiable functions for each variant. Recent research highlights the framework’s effectiveness in representing several combinatorial optimization problems. Inspired by these findings, we propose customized dataless neural networks for vertex-disjoint cycle cover variants. We derive a differentiable function for each variant and prove that the function will attain its minimum value if an exact solution is found for the corresponding problem variant. We also provide proof of the correctness of our approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

We have no data associated with this research.

References

  1. Abraham DJ, Blum A, Sandholm T (2007) Clearing algorithms for barter exchange markets: Enabling nationwide kidney exchanges. In: Proceedings of the 8th ACM conference on Electronic commerce, pp 295–304

  2. Akiba T, Iwata Y (2016) Branch-and-reduce exponential/FPT algorithms in practice: a case study of vertex cover. Theoret Comput Sci 609:211–225

    Article  MathSciNet  Google Scholar 

  3. Alkhouri Ismail R, Atia George K, Alvaro V (2022) A differentiable approach to the maximum independent set problem using dataless neural networks. Neural Netw 155:168–176

    Article  Google Scholar 

  4. Ashlagi I, Fischer F, Kash IA, Procaccia AD (2015) Mix and match: a strategyproof mechanism for multi-hospital kidney exchange. Games Econom Behav 91:284–296

    Article  MathSciNet  Google Scholar 

  5. Ashlagi I, Gamarnik D, Rees MA, Roth AE (2012) The need for (long) chains in kidney exchange. Technical report, National Bureau of Economic Research

  6. Ashlagi I, Roth AE (2014) Free riding and participation in large scale, multi-hospital kidney exchange. Theor Econ 9(3):817–863

    Article  MathSciNet  Google Scholar 

  7. Giorgio A, Pierluigi C, Giorgio G, Viggo K, Alberto M-S, Marco P (2012) Complexity and approximation: combinatorial optimization problems and their approximability properties. Springer, Cham

    Google Scholar 

  8. Bengio Y, Lodi A, Prouvost A (2021) Machine learning for combinatorial optimization: a methodological tour d’horizon. Eur J Oper Res 290(2):405–421

    Article  MathSciNet  Google Scholar 

  9. Blum A (2013) Algorithms: recitation notes. https://www.cs.cmu.edu/avrim/451f13/recitation/rec1016.txt

  10. Boppana R, Halldórsson MM (1992) Approximating maximum independent sets by excluding subgraphs. BIT Numer Math 32(2):180–196

    Article  MathSciNet  Google Scholar 

  11. Jena SK, Subramani K, Velasquez A (2023) Differentiable discrete optimization using dataless neural networks. In: Weili W, Jianxiong G, (eds.), Combinatorial Optimization and Applications - 17th International Conference, COCOA 2023, Hawaii, HI, USA, December 15-17, 2023, Proceedings, Part II, vol 14462 of Lecture Notes in Computer Science, pp 3–15. Springer

  12. Cornuejols G, Pulleyblank W (1980) A matching problem with side conditions. Discret Math 29(2):135–159

    Article  MathSciNet  Google Scholar 

  13. Cygan M, Fomin FV, Kowalik L, Lokshtanov D (2015) Dániel Marx. In: Michal P, Saket S (eds) Parameterized algorithms. Springer, Cham

    Chapter  Google Scholar 

  14. Dickerson JP, Manlove DF, Plaut B, Sandholm T, Trimble J (2016) Position-indexed formulations for kidney exchange. In: Proceedings of the 2016 ACM Conference on Economics and Computation, pp 25–42

  15. Ding Y, Ge D, He S, Ryan CT (2015) A non-asymptotic approach to analyzing kidney exchange graphs. In: Proceedings of the Sixteenth ACM Conference on Economics and Computation, pp 257–258

  16. Drori I, Kharkar A, Sickinger WR, Kates B, Ma Q, Ge S, Dolev E, Dietrich B, Williamson DP, Udell M (2020) Learning to solve combinatorial optimization problems on real-world graphs in linear time. In: 2020 19th IEEE International Conference on Machine Learning and Applications (ICMLA), pp 19–24

  17. Festa P (2014) A brief introduction to exact, approximation, and heuristic algorithms for solving hard combinatorial optimization problems. In 2014 16th International Conference on Transparent Optical Networks (ICTON), pp 1–20

  18. Flum Jörg GM (2006) Parameterized complexity theory. Texts in theoretical computer science. An EATCS series. Springer, Cham

    Google Scholar 

  19. Fomin FV, Kratsch D (2010) Exact exponential algorithms. Texts in theoretical computer science. An EATCS series. Springer, Cham

    Google Scholar 

  20. Garey MR, Johnson DS (1991) Computers and intractability: a guide to the theory of np-completeness. W. H. Freeman Company, San Francisco

    Google Scholar 

  21. Gaspers S (2010) Exponential time algorithms-structures, measures, and bounds. VDM

  22. Hartvigsen D (1984) Extensions of matching theory. PhD thesis, Carnegie Mellon University

  23. Hartvigsen D (1999) The square-free 2-factor problem in bipartite graphs. In: International Conference on Integer Programming and Combinatorial Optimization, pp 234–241. Springer

  24. Jena SK, Subramani K, Velasquez A (2024) A differential approach for several NP-hard optimization problems. In: International Workshop on Combinatorial Image Analysis, pp 68–80. Springer

  25. Lamm S, Sanders P, Schulz C, Strash D, Werneck RF (2016) Finding near-optimal independent sets at scale. In: 2016 Proceedings of the Eighteenth Workshop on Algorithm Engineering and Experiments (ALENEX), pp 138–150

  26. Li Z, Chen Q, Koltun V (2018) Combinatorial optimization with graph convolutional networks and guided tree search. In: Advances in neural information processing systems, p 31

  27. Mazyavkina N, Sviridov S, Ivanov S, Burnaev E (2021) Reinforcement learning for combinatorial optimization: A survey. Comput Oper Res 134:105400

    Article  MathSciNet  Google Scholar 

  28. Niedermeier R (2006) Invitation to fixed-parameter algorithms. Oxford University Press, Oxford

    Book  Google Scholar 

  29. Roth AE, Sönmez T, Ünver MU (2004) Kidney exchange. Quart J Econ 119(2):457–488

    Article  Google Scholar 

  30. Roth AE, Tayfun S, Utku ÜM (2005) Pairwise kidney exchange. J Econ Theor 125(2):151–188

    Article  MathSciNet  Google Scholar 

  31. Roth AE, Sönmez T, Utku Ünver M (2007) Efficient kidney exchange: coincidence of wants in markets with compatibility-based preferences. Am Econ Rev 97(3):828–851

    Article  Google Scholar 

  32. Segundo PS, Rodríguez-Losada D, Jiménez A (2011) An exact bit-parallel algorithm for the maximum clique problem. Comput Oper Res 38(2):571–581

    Article  MathSciNet  Google Scholar 

  33. Schuetz Martin JA, Kyle Brubaker J, Katzgraber Helmut G (2022) Combinatorial optimization with physics-inspired graph neural networks. Nat Mach Intell 4(4):367–377

    Article  Google Scholar 

  34. Toulis P, Parkes DC (2015) Design and analysis of multi-hospital kidney exchange mechanisms using random graphs. Games Econom Behav 91:360–382

    Article  MathSciNet  Google Scholar 

  35. William TT (1954) A short proof of the factor theorem for finite graphs. Can J Math 6:347–352

    Article  MathSciNet  Google Scholar 

  36. Wilder B, Dilkina B, Tambe M (2019) Melding the data-decisions pipeline: Decision-focused learning for combinatorial optimization. In: Proceedings of the AAAI Conference on Artificial Intelligence, vol 33, pp 1658–1665

Download references

Funding

This research was supported in part by the Defense Advanced Research Projects Agency through Grant HR001123S0001-FP-004.

Author information

Authors and Affiliations

  1. Department of Computer Science and Software Engineering, Miami University, Oxford, OH, USA

    Sangram K. Jena

  2. LDCSEE, West Virginia University, Morgantown, WV, USA

    K. Subramani

  3. Department of Computer Science, University of Colorado Boulder, Boulder, CO, USA

    Alvaro Velasquez

Authors
  1. Sangram K. Jena
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. K. Subramani
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Alvaro Velasquez
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to K. Subramani.

Ethics declarations

Conflict of interest

We declare that we have no Conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jena, S.K., Subramani, K. & Velasquez, A. Designing dataless neural networks for kidney exchange variants. Neural Comput & Applic 36, 22265–22275 (2024). https://doi.org/10.1007/s00521-024-10352-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-024-10352-6

Keywords