1 Introduction

From image classification [1] to natural language processing [2], data-driven models have rapidly revolutionized the way computers learn complicated mappings. The rapid developments in machine learning are being applied to the world of scientific computing by augmenting or replacing numerical algorithms based on mathematical models [3]. Even the Navier–Stokes equations for fluid flows, which are known to be difficult to simulate, are a current focus of interest for researchers looking to improve the simulation process via the application of machine learning [4].

Numerically solving the various differential equations within mathematical models often gives rise to computationally expensive algorithms. This is especially true as the dimension and complexity of the model increases. For such applications, scientific computing has produced a computationally attractive alternative for surrogating such models that rely on recent advances in artificial neural networks (ANNs) [5]. Despite the early introduction of ANNs for solving partial differential equations (PDEs) and ordinary differential equations (ODEs) in the late 90s [6], subsequent results in data-driven algorithms predominantly focused on other machine learning applications. It was not until the recent introduction of physics-informed neural networks (PINNs) in [7, 8] that led to a wave of interest in applying deep learning techniques to either approximate or enhance numerical solvers. This is because neural networks provide a data-based approach to modeling simulations that are more computationally efficient and tractable and do not require all governing mathematical elements to be accurately represented.

The basic PINN employs a data-driven network approach to solving PDEs by encoding the PDE residual as a soft constraint within the loss function used to train the neural network. Ensuing research tailored this concept to specific frameworks such as developments in PINNs targeting problems in fluid mechanics [9] and broadened the versatility of PINNs to handle other classes of PDEs as in [10, 11], which solve instances of fractional and time-dependent stochastic PDEs, respectively. Additional independent efforts tackled the curse of dimensionality as can be seen in [12] wherein the authors blend Galerkin [13] methods with the PINN process, as well as sought to hard code certain constraints (i.e., initial and boundary conditions) [14]. Despite the significant advancement, all research regarding PINNs and such similar approaches to solving PDEs focuses on learning the solution to a single instance of the PDE as they are techniques based on theorems that show neural networks to be universal approximations for functions [15, 16]. For the purposes of this paper, attention is shifted to learning an operator acting across a parameterized family of PDEs.

The work of Chen and Chen in [17] has gone largely unnoticed until recently within the machine learning community. The major theorem introduced by Chen and Chen provides a theoretical foundation for universal infinite dimensional nonlinear operator approximation by single-layer neural network-dubbed operator networks. This introduced the notion that the mapping between infinite dimensional function spaces can be represented by a neural network. Hence, the implication to physical models is a neural network that can learn the mapping between a state(s), condition(s), or other relevant physical data of the model to the solution.

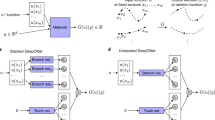
Currently, there are two primary competing types of operator networks based on Chen and Chen’s theorem: DeepONet [18] which was explicitly motivated by the work in [17] and its counterpart Fourier neural operator (FNO) [19]. The FNO was initially motivated by the idea of fundamental solutions of PDEs, while the DeepONet extends the operator network in [17] to deep networks in place of single layers. The basic structure of a DeepONet is a network comprised of two distinct networks known as a branch net and trunk net that are trained simultaneously. Built on the idea of using integral kernels, FNOs take advantage of the convolution theorem in Fourier analysis to parameterize the kernel integral operator in the spectral domain (computationally faster than convolution). A separate work has shown the theoretical justification for the FNO by Chen and Chen’s universal approximation theorem, but only in the case of invariant kernels [20].

The goal of this effort was to demonstrate the ability of a deep learning algorithm to efficiently provide a material’s thermal time-dependent response to incident laser radiation in both one and three spatial dimensions. More plainly, we desired a replacement for existing numerical simulators to provide expeditious real-time calculations in the laboratory environment. FNO networks were unable to learn the desired operator in all problems under the relevant application settings and for the selected materials and were unable to produce a successful approximation for either of the four-dimensional problems. DeepONet was implemented using deepXDE, [21], where testing revealed the operator network capable of learning the operator after significant training iterations (>10,000 epochs). A more recent version of DeepXDE’s DeepONet v1.8.4 demonstrated a working operator network in significantly less training time in contrast to older versions used in the initial experimentation. Operator networks such as FNO and DeepONet have previously only been applied to two or three-dimensional problems with the exception of Grady et al. in [22], wherein a model-parallel FNO is successfully able to learn an operator for function input on a four-dimensional domain. This is done by decomposing the domain for both the function input data and network weights.

For this article’s contribution, an improvement is introduced to the FNO that allows for the physics of the problem to inform the kernel integral operator instead of using a general convolution as the integral kernel resulting in the Fourier integral operator typically used in FNO networks. Neural operators are an excellent starting point as they are well designed for scientific simulations, able to extrapolate and predict solutions at new locations unseen during training [3]. This physics-informed kernel neural operator (PIKNO) network demonstrates similar or better convergence to DeepONet in the four test problems used in the application with the PIKNO being the only neural operator network to demonstrate any success with the four-dimensional domains for functional inputs, as FNO fails to converge. Hence, the PIKNO shows results comparable to that of DeepONet and is the only neural operator network to successfully learn an operator with input data defined in the four-dimensional setting (3D space and 1D time) with the exception of the model-parallel FNO in [22]. To the knowledge of the authors, it is the first neural operator network that does not require decomposing the domain for the input data. The numerical simulators being replaced relied on localizing the problem, which was computationally expensive, due to its ill-posed nature over the entire domain. Circumventing this challenge was a primary goal of implementing the operator network.

The remainder of the paper is structured as follows: Sect. 2 provides more details regarding operator networks as well as an overview of the numerical simulators utilized in the laboratory, focusing on two specific applications: the response of skin and ocular media to radiation exposure. Within Sect. 2, details of the heat equation, a fundamental component of the modeling process and the basis of the paper’s physics-informed approach, are elaborated upon. Section 3 delves into the construction and design of a neural operator, including a detailed architectural description and subsequent improvements. This is followed by the section detailing the numerical experiments and results. The Conclusion and Acknowledgements are in the final two sections.

Remark 1.1

The discovery of DeepXDE’s DeepONet v1.8.4 demonstrating drastically improved performance over older versions was made during the revision process, due to the lapse in time from experimentation to clearance of information for public release. All 4D experiments were updated to reflect the improved implementation of DeepONet, but the 2D experiments remain with the v1.4.0.

2 Background

2.1 Operator networks

In the brief time since their introduction, DeepONet and FNO have already been compared in a variety of settings to include the extensive and fair comparisons conducted in [23]. The FNO was originally praised for its fast convergence during training, excellent accuracy, and its use of the resolution invariant fast Fourier transform (FFT) (although it requires a uniform grid). DeepONet was subsequently improved with a faster implementation than FNO and was also shown to better handle irregular domains as the Fourier transform in FNO requires a regular structure. However, all comparisons were done with operators that act on at most two spatial dimensions with a maximum of three-dimensions for time-dependent problems. With the exception of three test problems in [23], these comparisons were conducted in the presence of ample data, most of which exceeded 1000 training instances, which follows from [17] wherein the theorems clearly suggest better accuracy from larger pools of data. A multiphysics electroconvection problem, predicting the surface vorticity of a flapping airfoil, and one of the regularized cavity flow problems demonstrate convergence for both operator networks with training data sets of 15, 28, and 10, respectively. For the test problems in [23], DeepONet was the better operator network with smaller relative \(L^2\) error in most of the test scenarios.

Additionally, a physics-informed DeepONet (PIDeepONet) [24] and physics-informed Fourier neural operator (PINO) [25] were introduced. Both augment their base network by including the physics element in the loss function. This integration of the physics into the soft constraint was inspired by PINNs, which is only designed to learn the mapping for the solution of a system under fixed conditions. Two notable further developments to operator networks include U-FNO [26] a modification of the original FNO structure designed for multiphase flow, and a hybrid network, Fourier DeepONet [27] that combines DeepONet with layers of FNO and U-FNO networks.

Several of these options showed promise as initial candidates for replacing the numerical simulators outlined in the subsequent section; however, each fell short in some way. Initial testing of incorporating the physics as a soft constraint yielded promising results [28], but ultimately produced mixed outcomes when applied to the context outlined in the following sections. The U-FNO modification was designed to target multiphase flow problems, and Fourier-DeepONet, introduced around the time of submission, would have added to the computational demand in a way that the research aim desired to avoid. Hence, the primary focus shifted to integrating the physics of the specific problem into the architecture as outlined in Sect. 3

2.2 PAC1D and SESE

Python Ablation Code (PAC1D) and Scalable Effects Simulation Environment (SESE) are comprehensive computer programs that conduct time-dependent simulations of a material’s response to incident laser radiation. While PAC1D assumes a one-dimensional spatial domain (Fig. 1), SESE calculates the distribution of radiative energy within the material and simulates the thermal energy diffusion for a three-dimensional spatial domain. Both algorithms are able to successfully model the relevant effects of laser radiation on an inhomogeneous structure [29, 30].

Time steps are adaptive and are controlled to ensure stability and bounded local errors, with a combination of explicit and implicit stepping methods used to optimize convergence speed. Within each time step, both programs employ iterative algorithms to solve the nonhomogeneous heat equation based on the physical characteristics of the material under a variety of boundary conditions. PAC1D uses the Crank-Nicolson method to solve the one-dimensional diffusion step [31], while SESE solves the heat equation in three-dimensions using the easily parallelized red-black successive over-relaxation (RBSOR) [32,33,34]. To model the radiative transport from the source, PAC1D is a more straight forward calculation relying on the material’s relevant physical characteristics due to the one-dimensional spatial domain, while SESE uses a Monte Carlo method to model the transport of radiative energy which can account for multiple sources [29, 30].

The application for this study focused on the thermal response from laser radiation exposure to skin and ocular media. PAC1D and SESE simulations were used to generate data employed for the purposes of training the operator networks. The three-layer skin model simulates the effect of thermal diffusion through the epidermis, dermis, and fat due to laser radiation exposure. While PAC1D and SESE can simulate different ocular media, the retina model was selected as its response throughout the simulation varies greatly from the response in the skin example due to the differences in tissue geometry and properties.

The material properties of both the skin and retina examples vary throughout the domain, with physical properties changing abruptly due to the various layers of biological material that lay adjacent to each other within each model. The physical characteristics of each material determine the spatial distribution of radiation absorbed, referred to as the radiative dose, I, with SI units \(W/m^3\). For the three-dimensional spatial domain, SESE also accounts for how the rays, small packets of energy that model the incident radiation, can erratically change direction due to the scattering, absorption, and anisotropy properties of the material [30].

Fig. 1
figure 1

PAC1D visual representation of 1D domain with layer dependent optical and mechanical properties

Full size image

2.3 Heat equation

The target problem for the purposes of this work is the successful construction of a deep learning surrogate for PAC1D and SESE, which both focus on a material’s response to laser irradiation. Thus, a primary element of the physical phenomenon being described is the transfer of heat energy throughout the material. This diffusion occurs both while the source of laser radiation is active and inactive, and this is why PAC1D and SESE contain a numerical method for solving the heat equation. Knowledge of the heat equation is also what motivated the specific elements of the operator network used in the experiments, with the relevant information presented below.

Consider the diffusion of heat in a bounded domain \(\Omega \subset \mathbb {R}^{d_s}\) for some \(d_s>0\). Given a constant heat conductivity, \(\alpha\), the heat equation

$$\begin{aligned} u_t(x,t)-\alpha \Delta u(x,t)=f(x,t), \,\, x \in \Omega ,\, t>0 \end{aligned}$$
(1)

governs the propagation of heat inside the body, where \(\Delta\) represents the Laplacian operator and u(x, t) is the temperature at the point (x, t). Moreover, letting \(\alpha =1\) without loss of generality, it is well-known that the function

$$\begin{aligned} \Phi (x,t) = \left\{ \begin{array}{cc} \left( \frac{1}{4\pi t}\right) ^{d_s/2} e^{-\frac{|x|^2}{4t}} & x \in \mathbb {R}^{d_s},\,t>0 \\ 0& x\in \mathbb {R}^{d_s},\,t<0 \end{array}\right. \end{aligned}$$
(2)

solves the homogeneous heat equation away from the singularity (0, 0) and is called the fundamental solution. Consequently, given the initial value problem

$$\begin{aligned} \left\{ \begin{array}{cc} u_t(x,t)-\Delta u(x,t)=0 & \text {in } \mathbb {R}^{d_s} \times (0,T) \\ u=g & \text {on } \mathbb {R}^{d_s} \times \left\{ t=0\right\} \end{array}\right. \end{aligned}$$
(3)

for some \(T>0\) and g continuous and bounded on \(\mathbb {R}^{d_s}\), the convolution

$$\begin{aligned} u(x,t) = \int _{\mathbb {R}^{d_s}}\Phi (x-y,t)g(y)dy \end{aligned}$$
(4)

solves (3) for each fixed \(y \in \mathbb {R}^{d_s}\). Turning attention back to the nonhomogeneous initial value problem, it can be shown that, given g continuous and bounded on \(R^d\) and with \(f, f_{x_j}, j=1,\dots ,d_s,\) continuous and bounded on \(R^{d_s}\times [0,T]\), the initial value problem

$$\begin{aligned} \left\{ \begin{array}{cc} u_t(x,t)-\Delta u(x,t)=f(x,t) & \text {in } \mathbb {R}^{d_s} \times (0,T) \\ u=g & \text {on } \mathbb {R}^{d_s} \times \left\{ t=0\right\} \end{array}\right. \end{aligned}$$
(5)

has a unique strong solution satisfying

$$\begin{aligned} u(x,t)= & \int _{\mathbb {R}^{d_s}}\Phi (x-y,t)g(y)dy\nonumber \\ & +\int _0^t\int _{\mathbb {R}^{d_s}}\Phi (x-y,t-s)f(y,s)dyds. \end{aligned}$$
(6)

For further details on the derivation and relevant proofs of these results, refer to [35, Ch. 2]. While the given framework for the heat equation that guarantees the fundamental solution in (2) is not exactly presented in the application, it was the motivation for the inclusion of the fundamental solution within the architecture used for the operator network.

All operator networks used for the experiments within this work were trained using data from the skin and retina models. The diffusion equation for these scenarios then takes the form

$$\begin{aligned} u_t(x,t) - \frac{\kappa }{\rho \cdot c_p} \Delta u(x,t) = \frac{1}{\rho \cdot c_p}I \end{aligned}$$
(7)

where \(\kappa\) is the thermal conductivity, \(\rho\) is the density, and \(c_p\) is the specific heat capacity for the material used, and I denotes the irradiation dose. Notice from (1), where \(\alpha = \frac{\kappa }{\rho \cdot c_p}\) and the source function becomes \(\frac{1}{\rho \cdot c_p}I\). For both the skin and retina models, the optical and mechanical properties of the material change with the structure of the biological tissue. This is more evident in the skin model, where the three adjacent layers epidermis, dermis, and fat have distinct responses to the laser irradiation and subsequent diffusion of thermal energy.

The boundary conditions for the physical domain are not shown for equation (7) as they vary depending on the specific application. The skin model assumes convective (Robin) boundary conditions for the portion of the physical domain that is exposed to air, and fixed (Dirichlet) boundary conditions for the remainder of the boundary for the 1D spatial domain. For the 3D spatial domain, the active boundary conditions are convective, radiative, and evaporative on different parts of the boundary. The data were generated assuming typical ranges for body and room temperatures. The retina model assumes infinite domain space outside the area of interest, which reflects the theoretical framework for the initial value problem in (3) that is satisfied by the fundamental solution. Practically, there must be a finite domain, and thus, the magnitude of a thermal gradient near the edge of the domain contributes a numerical error to the temperature solution due to the insulated boundary condition. The infinite domain is mimicked by increasing the domain size until the error contribution from the boundary in the region of interest converged on a sufficiently small value relative to the numerical error of the thermal solver.

Thus, under consideration of the setting in equation (7), the aim is for the neural network to learn the operator mapping dose to the solution \({\mathcal {G}}^\dagger : I \rightarrow u\), essentially the inverse of the PDE operator in equation (7). The dose function is parameterized by different irradiance (\(W/cm^2\)) levels in the 1D spatial setting and by differing values of power (watts) in the 3D spatial setting. The beam geometry in the 3D setting is left unchanged between experiments and is a matter of future investigations.

Remark 2.1

The abrupt change in layers of material within the skin example results in a discontinuous, piece–wise continuous, source term f(x, t). Continuity is a necessary assumption for implying the existence of the solution (1). This does not seem to affect the success of the models, but for theoretical justification for use of the heat kernel, a smooth version of the source term is assumed.

3 Methodology

3.1 Neural operators

Consider the more general setting where \(D\subset \mathbb {R}^{d_s}\times \mathbb {R}\) is a bounded and open set for some fixed \(d_s\in \mathbb {N}\) designating the spatial dimension and where \(d=d_s+1\) for convenience. The separate temporal dimension is due to the time-dependent nature of the problems considered, but not a necessary inclusion. Next, consider the functions

$$\begin{aligned}&a:D \rightarrow \mathbb {R}^{d_a}, \, \text { for }a \in {\mathcal {A}}(D;R^{d_a}) \end{aligned}$$
(8)
$$\begin{aligned}&u :D \rightarrow \mathbb {R}^{d_u}, \, \text { for } u \in {\mathcal {U}}(D;R^{d_u}) \end{aligned}$$
(9)

such that \({\mathcal {A}}\) and \({\mathcal {U}}\) are Banach spaces. Then, given the operator \({\mathcal {G}}^\dagger :{\mathcal {A}}\rightarrow {\mathcal {U}}\), operator networks seek to build an approximation for \({\mathcal {G}}^\dagger\) via the parametric map \({\mathcal {G}}:{\mathcal {A}}\times \Theta \rightarrow {\mathcal {U}}.\) Starting with a presentation of the evolution of neural operators, this paper concludes with a selection of operator network based on relative performance.

Under these considerations, the neural operator is defined, first introduced in [36], as \({\mathcal {N}}:{\mathcal {A}}\rightarrow {\mathcal {U}}\), where \({\mathcal {N}}\) is a composition mapping of depth \(L\in \mathbb {N}\) taking on the form

$$\begin{aligned} {\mathcal {N}}(a)={\mathcal {Q}}\circ {\mathcal {L}}_L\circ \dots \circ {\mathcal {L}}_2\circ {\mathcal {L}}_1\circ {\mathcal {R}}\circ a. \end{aligned}$$
(10)

Here, \({\mathcal {R}}:\mathbb {R}^{d_a} \rightarrow \mathbb {R}^{d_v}\) is a lifting operator while \({\mathcal {Q}}:\mathbb {R}^{d_v} \rightarrow \mathbb {R}^{d_u}\) is a projection operator, both acting locally and sandwiching a series of operators \({\mathcal {L}}_\ell :\mathbb {R}^{d_v} \rightarrow \mathbb {R}^{d_v}\) for \(\ell =1,2,\dots ,L\) that send their respective input, \(v_\ell\), to a successive state, \(v_{\ell +1}\). In particular, for a given \(\ell\) , this operator is defined as

$$\begin{aligned} {\mathcal {L}}_\ell :=\sigma \left( (W_\ell v_\ell )(x) + ({\mathcal {K}}(a;\theta )v_\ell )(x)\right) , \,\,\,\, \forall x\in D \end{aligned}$$
(11)

where \(W_\ell\) defines a linear mapping \(\mathbb {R}^{d_v}\rightarrow \mathbb {R}^{d_v}\), \(\sigma : \mathbb {R}\rightarrow \mathbb {R}\) is a nonlinear activation function acting component-wise, and \({\mathcal {K}}\) defines a mapping on \({\mathcal {A}}\times \Theta\) to the space of bounded linear operators on \({\mathcal {U}}(D;\mathbb {R}^{d_v})\), represented by \(L({\mathcal {U}}(D;\mathbb {R}^{d_v}),{\mathcal {U}}(D;\mathbb {R}^{d_v}))\). For practical purposes \(d_v\) is assumed greater than \(d_u\) and \(d_a\). Moreover, the operators \({\mathcal {Q}}\) and \({\mathcal {R}}\) can be sufficiently represented by shallow fully connected neural networks as shown in [19, 20].

Definition 3.1

(Kernel Integral Operator) Following the aforementioned framework, [19] defines kernel integral operators with the following specification for the operator \({\mathcal {K}}:\)

$$\begin{aligned} ({\mathcal {K}}(a;\theta )v_\ell )(x):=\int _D \kappa _\theta (x,y,a(x),a(y);\theta )v_\ell (y)dy, \,\,\,\, \forall x \in D \end{aligned}$$
(12)

where the integral kernel \(\kappa :\mathbb {R}^{2(d+d_a)} \rightarrow \mathbb {R}^{d_v\times d_v}\) is actually a neural network parameterized by \(\theta \in \Theta\) and learned from the data.

Motivated by fundamental solutions, the authors of [19] replace the integral kernel with \(\kappa (x,y) = \kappa (x-y)\) in order to obtain a convolution operator for (12). This allows for the subsequent introduction of Fourier integral operators which utilize the fast Fourier transform (FFT) in order to parameterize \(\kappa\) in Fourier space, taking advantage of the convolution theorem for faster training.

Definition 3.2

(Fourier Integral Operator) Applying the same framework as in 3.1, the Fourier integral operator is defined as

$$\begin{aligned} ({\mathcal {K}}(\theta )v_\ell )(x)={\mathcal {F}}^{-1}\left( R_\theta \cdot \left( {\mathcal {F}}v_\ell \right) \right) (x),\,\,\,\,\,\, \forall x \in D \end{aligned}$$
(13)

where \(R_\theta \in {\mathbb {C}}^{d_v\times d_v}\) is a matrix parameterized by \(\theta \in \Theta\) and indexed by \(k \in \mathbb {Z}^{d}\) such that \(R_\theta (k)={\mathcal {F}}(\kappa _\theta )(k)\). Conjugate symmetry is also imposed on \(R_\theta\) as \(\kappa\) is real-valued. As k represents the order of the discrete Fourier modes, the finite representation of the Fourier series is truncated at some \(k_{\max }\) such that \(|k_i|\le k_{\max } \text { for } i=1,\dots ,d+1 \text { and for } k \in \mathbb {Z}^{d}\) depending on the specific application and is usually fine-tuned during the testing phase. For more details on the selection of \(k_{\max }\), or the operator \({\mathcal {K}}\), refer to [19].

While the Fourier integral operator has seen great success within the FNO architecture at learning various operators, this has typically been in environments with ample datasets and in a one or two-dimensional spatial setting. Achieving the same success with smaller datasets and within the four-dimensional setting (three spatial dimension and one temporal) has not been as successful. This could be due in part to the complexities of simultaneous learning across both the parameters in the Fourier space and the linear mapping that comprise each step in an iteration of the FNO network. This, in conjunction with the fact that [20] seems to indicate an invariant kernel, suggested that the higher dimensional setting required either using another network, such as a graph kernel network [36], to learn the parameters for an appropriate kernel integral operator first followed by learning the parameters in the linear mapping (hypernetwork approach [37]), or a kernel integral operator that is motivated by the particular physics of the problem. This operator can then either serve as an initialization for the parameters in Fourier space or be held invariant. Both approaches were tested using a heat integral operator, defined below, that was motivated by the heat kernel described in Sect. 2.3.

Remark 3.1

A major advantage of the physics-informed kernel versus FNO is that FNO must maintain repeated complex multiplication of the elements in \(R_\theta\) with \({\mathcal {F}}v_\ell\) in order to coerce the parameters to maintain the necessary properties needed for the integral operator in the Fourier block. The number of multiplications needed increases exponentially in terms of the domain space over which the input functions are defined. This is a main reason the FNO architecture becomes unreasonable in higher dimensions. The physics-informed kernel does not increase complex multiplications in this manner, maintaining the same number in the higher dimension case as in the lower dimension.

Definition 3.3

(Heat Integral Operator) Let \(K(x,y,t) = \Phi (x-y,t)\), then define the operator

$$\begin{aligned} ({\mathcal {H}}v_\ell )(x)={\mathcal {F}}^{-1}\left( {\mathcal {F}}({\mathcal {S}}(K))(k) \cdot \left( {\mathcal {F}}v_\ell \right) \right) (x),\,\,\,\,\,\, \forall x \in D \end{aligned}$$
(14)

where, again, the discrete Fourier representation of K at \(k_{\max }\) is truncated, and with the necessary lifting operator \({\mathcal {S}}\), the composite mapping \({\mathcal {F}}\circ {\mathcal {S}}:\mathbb {R}^{d}\rightarrow {\mathbb {C}}^{k_{\max }\times d_v\times d_v}\) acts on the heat kernel, K. The lifting operator essentially stacks copies of the kernel to match the dimensions of the hidden layer input \(v_\ell\).

Thus, for the purposes of surrogating the numerical solvers PAC1D and SESE, the integral operator \({\mathcal {K}}\) was replaced with the physics-informed heat integral operator \({\mathcal {H}}\) resulting in a PIKNO. Since the Fourier transform of the heat kernel is well-known, \({\mathcal {F}} \circ {\mathcal {S}}\) was calculated analytically and hard-coded. The altered structure of the neural operator layer can be seen in Fig. 2. It is also worth noting that fundamental solutions of the heat equation assumes a constant conductivity coefficient which is not the case in this application. One can compute the numerical approximation to the fundamental solution for the variable coefficient case, but no analytic solution exists. However, the constant coefficient case is a good approximation if using the average over all regions of discontinuity as a base solution, and then training around this base solution by treating the variable coefficient case as perturbation around the constant coefficient case.

Fig. 2
figure 2

Diagram displaying the location of the physics-informed kernel within the neural operator layer

Full size image

The network PIKNO-H refers specifically to the PIKNO utilizing the heat integral operator. It demonstrated successful outcomes for both the retina model and the three-layer skin model under incidental laser exposure. Notably, its accuracy surpassed that of FNO and was comparable to results from DeepONet, especially in the four-dimensional setting with limited data availability.

To ensure thoroughness, PIKNO-H was also compared to other invariant integral operators using a variety of choices for \(R_\theta\) in (13). However, these alternative operators proved ineffective at learning \(G^\dagger\). Specifically, attempts to modify the exponential term or choose a kernel unrelated to the physics-informed selection resulted in the network’s inability to learn the operator effectively. In cases where changes from the heat-inspired kernel were more drastic, the results were even worse, particularly in higher dimensional settings and when updating the kernel through backpropagation [38].

Additionally, the possibility of using the heat integral operator with \({\mathcal {H}}\) as a point of initialization by allowing the operator to update during the network learning process was evaluated. However, the results indicated that holding \({\mathcal {H}}\) constant as the integral operator yielded optimal outcomes. It is also worthnoting that while the use of the physics-informed heat integral operator is specific to certain problems, the process of adapting the integral operator to better suit specific applications can be generalized to a broader class of parabolic PDEs.

Remark 3.2

The PIKNO is much different than the PIDeepONet and PINO as both PIDeepONet and PINO adopt the PINN strategy of including the PDE residual as a soft constraint, whereas the PIKNO does not employ any use of the PDE. Instead the PIKNO is altering the integral kernel, as a result of the physics of the specific problem. This same integral kernel can then be used without alteration even as the PDE changes for various specific applications.

Remark 3.3

For the purposes of our experiments, it is worthnoting that D is a rectangular domain and the work in [20] is proven under the assumption that the domain is a d-dimensional torus, but the proofs therein are generalizable to rectangular domains. Moreover, certain irregular domains such as the two-dimensional triangle or a star-shaped domain with a hole in it were shown in [23] to cause convergence issues for the FNO network, but that is not an issue under our assumption for D.

4 Numerical experiments and results

In this section, the numerical experiments are described to demonstrate the effectiveness of the PIKNO at surrogating the numerical algorithms PAC1D and SESE in both the two-dimensional and four-dimensional settings and under the constraint of small datasets. For both frameworks, the PIKNO network is learning the operator that maps the radiative dose to the solution of the heat equation (7) under incidental laser exposure. A comparison was performed with other well-known operator networks DeepONet and FNO as well as with the PIKNO heat integral operator \({\mathcal {H}}\) set to other initializations for the kernel integral operator outside of the random initialization employed by FNO. A comparison between holding the heat integral operator invariant versus allowing \({\mathcal {H}}\) to serve as an initialization and updating the heat integral operator via backpropagation is also demonstrated.

For these experiments, the focus is on two physical models: the retina model and the three-layer skin model. In both cases, the physical domain is represented as a rectangular slice of either the retina or the skin, with the material properties defining the physical characteristics of the domain. To simulate real-life scenarios of incidental laser exposure, Robin boundary conditions are applied on the side of the domain exposed to the laser, while Dirichlet boundary conditions are applied on the opposite side.

The data for these experiments were obtained from two sources: PAC1D for the two-dimensional setting and SESE for the four-dimensional setting. PAC1D primarily served as an initial testing ground for the SESE experiments, and its results are included for completeness. The \(L^2\) relative error was used as the test metric for all experiments, following the methodology described in [19, 23].

In implementing the optimal PIKNO for various problem settings, a network with four stacked PIKNO layers (see Fig. 2) was found to be most effective. Each layer employed hyperbolic tangent as the output activation function, which is a departure from the usual choice of Gaussian error linear unit (GeLU) for FNO layers, as described in [3].

Remark 4.1

In both the 1D and 3D time-dependent problems, time as input was included in the FNO and PIKNO thus performing the convolution in both space and time as opposed to performing the convolution in the space domain only and using an RNN for propagating in time as the latter usually produces worse error.

4.1 2D retina and skin

For both the retina and three-layer skin model in PAC1D, a simulation was run to generate only 22 samples of radiative dose functions resulting from a laser irradiance ranging from \([1\times 10^7 \frac{W}{\mathrm {cm^2}},1.01 \times 10^7 \frac{W}{\mathrm {cm^2}}]\) and equally spaced across the range. Each simulation ran for a total of one second across a one-dimensional spatial grid of 250 equally spaced points for a total of 1000 time steps in the three-layer skin example. The retina data have 1000 time steps and 200 steps on the spatial domain. The source irradiation was on for half the time with the remainder of the time allowing for the heat diffusion process to continue with no source term. For both models, only 16 data samples were used for training purposes and six for testing.

Table 1 \(L^2\) error for 2D (1D space and 1D time) problems
Full size table
Table 2 \(L^2\) error for 2D (1D space & 1D time) problems on the more course mesh
Full size table

During the training process, the operator networks learned the mapping to the solution of equation (7) from the dose function values. Different training runs were conducted across different discretizations for the (x, t) domain with the results from the full grid shown in Table 1:\(250\times 1000\) for the three-layer skin problem, and \(200\times 1000\) for the retina problem. The networks were also trained on more sparse but uniform grids across the domain making up only 20% of total domain points available from numerical simulations. Table 2 shows the results from training networks using dose function data taken on course grids of size \(50\times 200\) for the skin problem and \(40\times 200\) for the retina problem. The results between the various discretizations were similar, with computational time naturally in favor of the more coarse space and time grid. The FNO, PIKNO(upd), and PIKNO(const) converged within 0.01 of the final relative error shown in Tables 1, 2 in fewer than 300 epochs while DeepONet required significantly more iterations in order to reach a relative error that was comparable with the other operator networks. Results from at least 1000 training iterations were included with the extra 10,000 required by DeepONet for convergence in order to achieve similar results as the FNO.

It is important to note that DeepONet was faster in iterating through the training loop than FNO by an approximate factor of 10. Thus, the 10,000 epochs required by DeepONet were comparable in computational time to 1000 epochs of FNO. The PIKNO improved the backpropogation time from FNO on average by a factor of 25.7 with a sample variance of 0.8, and the optimizer step by a factor of 2.5 on average with a variance of 0.01. This, paired with PIKNOs ability to converge in significantly fewer epochs than FNO, made it appealing as a substitute for the numerical simulators PAC1D and SESE.

Given enough time, however, the DeepONet actually outperforms the other networks in some cases. In particular, the DeepONet when trained on the dose function corresponding to the more coarse grid actually reaches a relative error of 0.0034 after 100,000 epochs for the skin problem. This exceeds the performance of the other operator networks for this same example. The corresponding image of the trained DeepONet for the skin problem on the more coarse grid can be seen in Fig. 3b, in comparison with the FNO image in Fig. 3a generated after only 1,000 epochs. The DeepONet trained on the same resolution for the retina problem, however, sees no improvement in the relative error after 100,000 epochs.

The ocular medium has a significantly different responses to the laser irradiation in comparison with skin resulting in an excellent test of the operator network’s flexibility. The FNO was unable to converge at all to a suitable network for the fine discretization of the space and time grid. DeepONet appears to produce a favorable result as it converges to a relative error of less than 0.04; however, further inspection of the network shows that the solution approximations produced by DeepONet are constant functions and miss the key features of the true solutions. The solutions to the retina problem, for all of the dose inputs, are mostly constant in terms of temperature throughout the spatial temporal domain with the exception of two relatively small areas of the spatial domain that have drastic spikes that gradually decrease in time due to the diffusion. The DeepONet misses these spikes completely in favor of a function that is constant everywhere, while both the PIKNO-H(upd) and the PIKNO-H(const) are able to pick up the essential shape of these temperature peaks. The coarse grid only contains the information for the larger peak, with the smaller temperature peak missed completely by the coarse data. Thus, the FNO is able to converge to a network with small relative error, but whose output completely misses the primary temperature peak. In a similar manner as the DeepONet, the solution approximations produced by the FNO network maintain a constant temperature for all x and t and miss the spike in temperature that is in the actual solution.

Fig. 3
figure 3

Comparison of the predicted temperature (Kelvin) for the 2D three-layer skin model using (a) FNO network after 1000 epochs and (b) DeepONet after 100,000. Both figures generated from networks trained using dose values taken on the more coarse grid

Full size image

The other operator networks had some success in the lower dimensional setting with a comparison of the images shown in Fig. 3. The FNO, however, was unable to produce a successful network for the retina model as the function values tend to be mostly constant with the exception of a drastic spike in values at a relatively small part of the domain. This caused issues for the Fourier transform even when all Fourier modes were included. The DeepONet was successful at learning the operator for both the retina and skin models, but only after allowing the training to run significantly more epochs than what was required from the other operator networks. However, this was implemented with DeepONet v1.4.0 in the DeepXDE library, and it should be noted versions released post experimentation have demonstrated significant reduction in training time. Also, DeepONet is well-known to be much faster per training epoch than FNO. Even so, the computational demand for training these operator networks made them sub-optimal for surrogating the existing numerical algorithm PAC1D. The 2D results are included out of completeness, but the main interest lies in the 4D simulation domain since radial diffusion cannot often be neglected due to beam diameter or exposure duration. As such, the 2D setting served mostly for the purposes of providing a testing ground prior to implementing models in the higher dimensional setting.

4.2 4D retina and skin

For the 4D case, SESE simulations generated only eight data samples of radiative dose calculated using the beam geometry and power (watt) for both the retina and three-layer skin models. For these samples, the radiative dose resulted from altering the power delivered, while holding the wavelength and pulse duration constant. There are nine time steps sampled across one second with the laser source active for the entire second for the skin example. For the retina case, there were 11 time steps sampled across one millisecond, again, with the laser active for the entire millisecond. Various discretizations were used during experimentation, but the results were similar. Laser power (watt) varied between models for the eight samples used and are as follows:

$$\begin{aligned} \text {Retina : }&\left\{ 24.5, 28, 35, 42, 49, 56, 70, 84\right\} \\ \text {Skin : }&\left\{ 250, 500, 750, 1000, 1250, 1500, 1750, 2000\right\} . \end{aligned}$$

For training purposes, five samples were used with three withheld for testing.

The spatial domain for the retina and skin model is a \(25\times 25\times 70\) grid for (x, y, z) with the point of exposure from the laser radiation occurring along the Z-axis. The more coarse discretization shown here for the four-dimensional setting had the added benefit of being able to train on a local machine with only 32 GB of RAM. Moreover, the PIKNO, still retains the advantages of the FNO of being able to be tested on a finer mesh than the one used during training.

Table 3 \(L^2\) and \(L^\infty\) error for 4D (3D space and 1D time) three-layer skin problem after 1000 training iterations
Full size table
Table 4 \(L^2\) and \(L^\infty\) error for 4D (3D space and 1D time) retina problem after 1000 training iterations
Full size table

The results in Tables 3,  4 show the PIKNO-H(upd) as the model with the minimal \(L^2\) error, although the PIKNO-H(const) produced similar results more efficiently as the network has significantly fewer trainable parameters. More precisely, for the three-layer skin model, Table 5 shows the PIKNO-H(const), which only has 3481 network parameters, is a reduction in the number of parameters of four orders of magnitude from the FNO network. Thus, while PIKNO-H(upd) has the slight edge regarding performance, the PIKNO-H(const) has the advantage of a much smaller training time. Although PIKNO-H(upd) still only has roughly half the trainable parameters as FNO for the same model. DeepONet also demonstrated decent success with the better \(L^\infty\) error for the three-layer problem and had comparable results in the retina problem. The high dimensionality and resulting complexity of the parameter space also resulted in the FNO being unable to converge.

Table 5 Number of parameters for each of the three-layer skin models
Full size table

The operator networks were also trained only over the initial time steps when the source term was presented. The latter time steps modeling thermal diffusion without any source term were omitted. It was speculated that the DeepONet and FNO would perform better in this scenario due to the smaller data sets and less variability in this initial phase of the problem. Indeed, the results displayed in Tables 6, 7 were more of a mixed bag and DeepONet, PIKNO-H(upd), PIKNO-H(const) produced a workable operator network after only 500 training instances. The corresponding plots of the reduction in relative \(L^2\) error during the 500 iterations are displayed in Fig. 4. In this instance, the PIKNO-H(upd) and PIKNO-H(const) are indistinguishable.

Continuing to train the algorithm, past 1000 iterations yield marginal improvements in the relative error, but improved the quality of the images created with the exception of FNO networks that were unable to learn the problem even past 10,000 training iterations. The images generated in Figs. 5, 6 were created comparing the trained PIKNO-H(upd) and DeepONet models after learning for 5000 iterations in comparison with the image generated by SESE. The only consistent differences in the images generated by PIKNO-H versus DeepONet is that the PIKNO-H appeared to better mimic the erratic change in direction of the rays due to the scattering, absorption, and anisotropy properties of the material while the DeepONet created a smoother, more even diffusion throughout the material. This can be observed when comparing to the SESE image shown on the bottom row of both figures.

Table 6 \(L^2\) and \(L^\infty\) error for 4D (3D space and 1D time) three-layer skin problem after 500 training iterations with only the initial time steps where the source term is active
Full size table
Table 7 \(L^2\) and \(L^\infty\) error for 4D (3D space and 1D time) retina problem after 500 training iterations with only the initial time steps where the source term is active
Full size table

As for the other operator networks used as the baseline comparison, FNO struggled to find optimal models in the 4D environment, while DeepONet demonstrated comparable results, with PIKNO-H(upd) demonstrating a slight advantage. FNO failed to produce a successful network for the purpose of surrogating the numerical algorithm SESE in both the three-layer skin and retina settings. Several different implementations were tested for all networks, but changing the network structure, increasing the width of the networks, or the modes in the FNO were all met with the same results. It is possible that there are other higher dimensional settings that would have resulted in a more favorable outcome for the FNO network, but not for the particular design of application here. For all of the tables, the minimum errors are highlighted using bold typeface.

Fig. 4
figure 4

A comparison of L2 relative error reduction between the PIKNO, DeepONet, and FNO models per iteration

Full size image
Fig. 5
figure 5

XY-slice of predicted outputs after 5000 training iterations by PIKNO-H(upd) (top) and DeepONet (middle) for the 4D three-layer skin example across four time steps compared to SESE (bottom)

Full size image
Fig. 6
figure 6

XZ-slice of predicted outputs after 5000 training iterations by PIKNO-H(upd) (top) and DeepONet (middle) for the 4D three-layer skin example across four time steps compared to SESE (bottom)

Full size image

5 Conclusion

This article describes an operator network based on the FNO network structure, but which uses a physics-informed approach to the kernel integral operator. The resulting network, PIKNO-H, could then be implemented as is with the integral operator acting invariantly on the input data during the training process, or the kernel of the integral operator could be updated. Updating the kernel led to better results in the 4D setting, but caused issues in the 2D setting since the network had a relative error of 0.2003 when tested on the three-layer skin data. The PIKNO-H(const) was the optimal network in the 2D setting and maintained excellent results in the 4D setting as well as having the advantage of only a few thousand trainable parameters producing a training time that is less than half of what the PIKNO-H(upd) required. Moreover, DeepONet was the only other operator network to demonstrate success in the 4D setting, as FNO was unable to learn the operator for the higher dimension, with the PIKNO operators producing similar or better results as DeepONet. This demonstrates the PIKNO’s effectiveness at providing computationally efficient approximations in place of SESE, whose calculation of simulations on a similar scale takes considerable time. It is worthnoting that while the applications of interest here dealt with a more smooth boundary and connected region, more rough and complex domains can be approximated by smooth boundaries. This allows for a path in generalizing the use of the PIKNO to learn the operator acting on functions with arbitrary geometries.

In theory, the same integral kernel could be tested in any environment that depends on a thermal diffusion process, but the ability of the PIKNO to generalize to other situations depends on selecting an integral kernel suited to the physics of the specific model. While the same integral kernel is shown to be successful in producing great results in two-different scenarios, a matter of future interest would be to establish this an integral kernel for models where the physics do not lend themselves to such an obvious choice. Such a network could benefit from investigating GKNs and employing them within the neural operator framework.