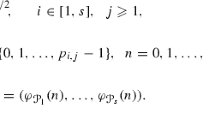Abstract
Assume that α is an irrational number with continued fraction expansion [a0;a1, . . .] and convergents  ,n= 0, 1 . . . . Every positive integer N has a unique expansion N=b0q0+b1q1+ . . . +b
m
q
m
, where the digits b
i
are nonnegative integers with b0<a1,b
i
≤a
i
+1 and such that b
i
=a
i
+1 implies b
i
−1=0, the so-called Ostrowski expansion of N to base α. On the other hand let c[0,
x
) be the characteristic function of the half-open interval [0,x) and let
,n= 0, 1 . . . . Every positive integer N has a unique expansion N=b0q0+b1q1+ . . . +b
m
q
m
, where the digits b
i
are nonnegative integers with b0<a1,b
i
≤a
i
+1 and such that b
i
=a
i
+1 implies b
i
−1=0, the so-called Ostrowski expansion of N to base α. On the other hand let c[0,
x
) be the characteristic function of the half-open interval [0,x) and let

be the L2-discrepancy of the sequence (nα) mod 1, where {y} denotes the fractional part of the real number y. In this paper, we give an explicit formula for D*(2)N(α) entirely in terms of the digits b0, . . . ,b m . This formula enables one to compute the L2-discrepancy in at most O(log4N) steps, where the O-constant does not depend on α, while in the classical formulae for the L2-discrepancy N2/2 calculation steps are necessary. The fastest algorithm so far was found by S. Heinrich [3] and works (for all sequences) in O(N log N) steps.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
P. Barkan (1977) ArticleTitleSur les sommes de Dedekind et les fractions continues finies C. R. Acad. Sci. Paris, Sér. A 284 923–926 Occurrence Handle0347.10007 Occurrence Handle55 #7897
C. Baxa J. Schoißengeier (2002) ArticleTitleCalculation of improper integrals using (nα)-sequences Monatsh. Math. 135 265–277 Occurrence Handle2003h:11084
S. Heinrich (1996) ArticleTitleEfficient algorithms for computing the L2-discrepancy Math. Comp. 65 IssueID216 1621–1633 Occurrence Handle10.1090/S0025-5718-96-00756-9 Occurrence Handle0853.65004 Occurrence Handle97a:65024
D. Hickerson (1977) ArticleTitleContinued fractions and density results for Dedekind sums J. Reine Angew. Math. 290 113–116 Occurrence Handle0341.10012 Occurrence Handle55 #12611
D. E. Knuth (1977) ArticleTitleNotes on generalized Dedekind sums Acta Arith. 33 297–325 Occurrence Handle0326.10007 Occurrence Handle58 #5483
L. Kuipers H. Niederreiter (1974) Uniform distribution of sequences Wiley New York
Roçadas, L., Schoißengeier, J.: Bernoulli polynomials and (nα)-sequences (to appear).
J. Schoißengeier (1984) ArticleTitleOn the discrepancy of (nα) Acta Arithm. 44 241–279 Occurrence Handle0506.10031
J. Schoißengeier (2000) ArticleTitleAnother proof of a theorem of J. Beck Monatsh. Math. 129 147–151 Occurrence Handle0991.11041 Occurrence Handle2001a:11120
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Prof. W. G. Nowak on the occasion of his 50th birthday.
Rights and permissions
About this article
Cite this article
Roçadas, L., Schoißengeier, J. An Explicit Formula for the L2-Discrepancy of (nα)-Sequences. Computing 77, 113–128 (2006). https://doi.org/10.1007/s00607-005-0143-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00607-005-0143-1