Skip to main content
Springer Nature Link
Log in

Point Values Hermite Multiresolution for Non-smooth Noisy Signals

  • Published:
Computing Aims and scope Submit manuscript

Abstract

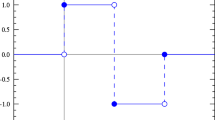
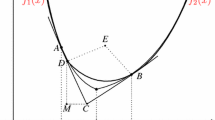
In this paper, a nonlinear interpolation is used in order to compute adaptively derivatives from the discrete information of any signal. Using these derivatives a multiresolution based on Hermite interpolation is performed for compressing the signal. The way in which the derivatives are approximated is crucial when noise or singularities appear.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Amat, S., Donat, R., Liandrat, J., Trillo, J. C.: Analysis of a new nonlinear subdivision scheme. Applications in image processing. Found. Comp. Math. (2005, accepted).

  • F. Aràndiga A. Baeza R. Donat (2004) ArticleTitleDiscrete multiresolution based on Hermite interpolation: Computing derivatives Comm. Nonlinear Sci. Num. Simulation 9 263–273 Occurrence Handle10.1016/S1007-5704(03)00116-3

    Article  Google Scholar 

  • F. Aràndiga R. Donat (2000) ArticleTitleNonlinear multi-scale decompositions: The approach of A. Harten Num. Algorith. 23 175–216 Occurrence Handle10.1023/A:1019104118012

    Article  Google Scholar 

  • A. Harten (1996) ArticleTitleMultiresolution representation of data II: General framework SIAM J. Numer. Anal. 33 1205–1256 Occurrence Handle10.1137/0733060 Occurrence Handle0861.65130 Occurrence Handle97h:65078

    Article  MATH  MathSciNet  Google Scholar 

  • R. Warming R. Beam (2000) ArticleTitleDiscrete multiresolution analysis using Hermite interpolation: Biorthogonal multiwavelets SIAM J. Sci. Comp. 22 1269–1317 Occurrence Handle10.1137/S1064827597315236 Occurrence Handle2001e:42055

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Ecole supérieure de Mécanique de Marseille, 13451, Marseille Cedex 20, France

    I. Ali

  2. Departamento de Matemática Aplicada y Estadística, Universidad Politécnica de Cartagena, 30203, Cartagena, Spain

    S. Amat

  3. Departamento de Matemática Aplicada y Estadística, Universidad Politécnica de Cartagena, 30203, Cartagena, Spain

    J. C. Trillo

Authors
  1. I. Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. Amat
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. J. C. Trillo
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to I. Ali.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ali, I., Amat, S. & Trillo, J.C. Point Values Hermite Multiresolution for Non-smooth Noisy Signals. Computing 77, 223–236 (2006). https://doi.org/10.1007/s00607-005-0159-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00607-005-0159-6

AMS Subject Classifications

Keywords