Skip to main content
SpringerLink
Log in

Finite iterative algorithms for the generalized Sylvester-conjugate matrix equation \({AX+BY=E\overline{X}F+S}\)

  • Published:
Computing Aims and scope Submit manuscript

Abstract

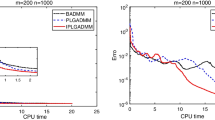
This paper investigates the generalized Sylvester-conjugate matrix equation, which includes the normal Sylvester-conjugate, Kalman–Yakubovich-conjugate and generalized Sylvester matrix equations as its special cases. An iterative algorithm is presented for solving such a kind of matrix equations. This iterative method can give an exact solution within finite iteration steps for any initial values in the absence of round-off errors. Another feature of the proposed algorithm is that it is implemented by original coefficient matrices. By specifying the proposed algorithm, iterative algorithms for some special matrix equations are also developed. Two numerical examples are given to illustrate the effectiveness of the proposed methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Horn RA, Johnson CR (1990) Matrix analysis. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  2. Bevis JH, Hall FJ, Hartwing RE (1987) Consimilarity and the matrix equation \({A\overline{X}-XB=C}\) . In: Current trends in matrix theory (Auburn, Ala., 1986). North-Holland, New York, pp 51–64

  3. Hong YP, Horn RA (1988) A canonical form for matrices under consimilarity. Linear Algebra Appl 102: 143–168

    Article  MATH  MathSciNet  Google Scholar 

  4. Huang L (2001) Consimilarity of quaternion matrices and complex matrices. Linear Algebra Appl 331: 21–30

    Article  MATH  MathSciNet  Google Scholar 

  5. Jiang T, Cheng X, Chen L (2006) An algebraic relation between consimilarity and similarity of complex matrices and its applications. J Phys A Math Gen 39: 9215–9222

    Article  MATH  MathSciNet  Google Scholar 

  6. Bevis JH, Hall FJ, Hartwig RE (1988) The matrix equation \({A\overline{X}-XB=C}\) and its special cases. SIAM J Matrix Anal Appl 9(3): 348–359

    Article  MATH  MathSciNet  Google Scholar 

  7. Wu AG, Duan GR, Yu HH (2006) On solutions of XF − AX = C and \({XF-A\overline{X}=C}\) . Appl Math Appl 182(2): 932–941

    MathSciNet  Google Scholar 

  8. Jiang T, Wei M (2003) On solutions of the matrix equations X − AXB = C and \({X-A\overline{X}B=C}\) . Linear Algebra Appl 367: 225–233

    Article  MATH  MathSciNet  Google Scholar 

  9. Wu AG, Fu YM, Duan GR (2008) On solutions of the matrix equations V − AVF = BW and \({V-A\overline{V}F=BW}\) . Math Comput Model 47(11–12): 1181–1197

    Article  MATH  MathSciNet  Google Scholar 

  10. Wu AG, Feng G, Hu J, Duan GR (2009) Closed-form solutions to the nonhomogeneous Yakubovich-conjugate matrix equation. Appl Math Appl 214: 442–450

    MATH  MathSciNet  Google Scholar 

  11. Wu AG, Feng G, Duan GR, Wu WJ (2010) Closed-form solutions to Sylvester-conjugate matrix equations. Comput Math Appl 60(1): 95–111

    Article  Google Scholar 

  12. Fletcher LR, Kautasky J, Nichols NK (1986) Eigenstructure assignment in descriptor systems. IEEE Trans Autom Control 31(12): 1138–1141

    Article  MATH  Google Scholar 

  13. Syrmos VL, Lewis FL (1993) Output feedback eigenstructure assignment using two Sylvester equations. IEEE Trans Autom Control 38(3): 495–499

    Article  MATH  MathSciNet  Google Scholar 

  14. Carvalho J, Datta K, Hong Y (2003) A new algorithm for full-rank solution of the Sylvester-observer equation. IEEE Trans Autom Control 48(12): 2223–2228

    Article  MathSciNet  Google Scholar 

  15. Wu AG, Duan GR (2006) Design of generalized PI observers in descriptor linear Systems. IEEE Trans Circuits Syst I: Regular Papers 53(12): 2828–2837

    Article  MathSciNet  Google Scholar 

  16. Wu AG, Duan GR, Fu YM (2007) Generalized PID observer design for descriptor linear systems. IEEE Trans Syst Man Cybern B: Cybern 37(5): 1390–1395

    Article  Google Scholar 

  17. Tsui CC (1987) A complete analytical solution to the equation TA − FT = LC and its applications. IEEE Trans Autom Control AC-32(8): 742–744

    Article  MathSciNet  Google Scholar 

  18. Duan GR (1996) On the solution to Sylvester matrix equation AV + BW = EVF. IEEE Trans Autom Control 41(4): 612–614

    Article  MATH  Google Scholar 

  19. Zhou B, Duan GR (2006) A new solution to the generalized Sylvester matrix equation AV − EVF = BW. Syst Control Lett 55(3): 200–208

    Article  MathSciNet  Google Scholar 

  20. Wu AG, Duan GR, Zhou B (2008) Solution to generalized Sylvester matrix equations. IEEE Trans Autom Control 53(3): 811–815

    Article  MathSciNet  Google Scholar 

  21. Wu AG, Duan GR (2007) Kronecker maps and Sylvester-polynomial matrix equations. IEEE Trans Autom Control 52(5): 905–910

    Article  MathSciNet  Google Scholar 

  22. Bischof C, Datta BN, Purkayastha A (1996) A parallel algorithm for the Sylvester observer equation. SIAM J Sci Comput 17: 686–698

    Article  MATH  MathSciNet  Google Scholar 

  23. Ding F, Chen T (2005) Gradient based iterative algorithms for solving a class of matrix equations. IEEE Trans Autom Control 50(8): 1216–1221

    Article  MathSciNet  Google Scholar 

  24. Ding F, Liu PX, Ding J (2008) Iterative solutions of the generalized Sylvester matrix equations by using the hierarchical identification principle. Appl Math Comput 197: 41–50

    Article  MATH  MathSciNet  Google Scholar 

  25. Wu AG, Feng G, Duan GR, Wu WJ (2010) Iterative solutions to coupled Sylvester-conjugate matrix equations. Comput Math Appl 60(1): 54–66

    Article  Google Scholar 

  26. Zhou B, Duan GR, Li ZY (2009) Gradient based iterative algorithm for solving coupled matrix equations. Syst Control Lett 58: 327–333

    Article  MATH  MathSciNet  Google Scholar 

  27. Hou JJ, Peng ZY, Zhang XL (2006) An iterative method for the least squares symmetric solution of matrix equation AXB = C. Numer Algorithm 42: 181–192

    Article  MATH  MathSciNet  Google Scholar 

  28. Peng ZY (2005) An iterative method for the least squares symmetric solution of the linear matrix equation AXB = C. Appl Math Comput 170: 711–723

    Article  MATH  MathSciNet  Google Scholar 

  29. Zhang X (2004) Matrix analysis and applications. Tsinghua University Press, Beijing

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Information and Control Research Center, Harbin Institute of Technology Shenzhen Graduate School, Shenzhen, 518055, People’s Republic of China

    Ai-Guo Wu

  2. Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin, 150001, People’s Republic of China

    Ai-Guo Wu, Guang-Ren Duan & Yan-Ming Fu

  3. National Key Laboratory of Antennas and Microwave Technology, Xidian University, Xi’an, 710071, People’s Republic of China

    Wei-Jun Wu

Authors
  1. Ai-Guo Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guang-Ren Duan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yan-Ming Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wei-Jun Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ai-Guo Wu.

Additional information

Communicated by C.C. Douglas.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wu, AG., Duan, GR., Fu, YM. et al. Finite iterative algorithms for the generalized Sylvester-conjugate matrix equation \({AX+BY=E\overline{X}F+S}\) . Computing 89, 147–170 (2010). https://doi.org/10.1007/s00607-010-0100-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00607-010-0100-5

Keywords

Mathematics Subject Classification (2000)

Search

Navigation