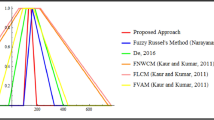
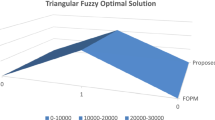
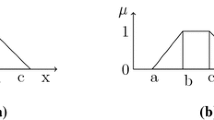Abstract
Several problems involving uncertainties can be modeled with fuzzy numbers according to the type of these uncertainties. It is natural to express the solution to such a problem with fuzzy numbers. In this study, we consider the fully fuzzy transportation problem. All input parameters of the problem are expressed with fuzzy numbers given in the parametric form. We propose a new heuristic algorithm to approximate the fuzzy optimal solution. The fuzzy problem is solved by transforming it into two independent parametric problems with the proposed method. We first divide the interval [0, 1] into a sufficiently large number of equal intervals, then write a linear programming problem for each partition point and solve these problems by transforming them into transportation problems. The proposed algorithm is supported by examples.



















Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
Data sharing does not apply to this study as no datasets were generated or analyzed during the current study.
References
Hitchcock FL (1941) Distribution of a product from several sources to numerous locations. J Math Phys 20:224–230
Hosseini A, Pishvaee MS (2022) Capacity reliability under uncertainty in transportation networks: an optimization framework and stability assessment methodology. Fuzzy Optim Decis Mak 21(3):479–512
Stanojevic B (2022) Extension principle-based solution approach to full fuzzy multi-objective linear fractional programming. Soft Comput 26(11):5275–5282
Saikia B, Dutta P, Talukdar P (2023) An advanced similarity measure for Pythagorean fuzzy sets and its applications in transportation problem. Artif Intell Rev 56:12689–12724
Jansi Rani J, Manivannan A, Dhanasekar S (2023) Interval valued intuitionistic fuzzy diagonal optimal algorithm to solve transportation problems. Int J Fuzzy Syst 25:1465–1479
Kartli N, Bostanci E, Guzel MS (2023) A new algorithm for optimal solution of fixed charge transportation problem. Kybernetika 59(1):45–63
Sun L (2022) Modeling and evolutionary algorithm for solving a multi-depot mixed vehicle routing problem with uncertain travel times. J Heuristics 28(5–6):619–651
ÓhÉigeartaigh M (1982) A fuzzy transportation algorithm. Fuzzy Sets Syst 8(3):235–243
Chanas S, Kolodziejczyk W, Machaj A (1984) A fuzzy approach to the transportation problem. Fuzzy Sets Syst 13(3):211–221
Chanas S, Kuchta D (1996) A fuzzy approach to the transportation problem. Fuzzy Sets Syst 82(3):299–305
Tada M, Ishii H (1996) An integer fuzzy transportation problem. Comput Math Appl 31(8):71–87
Liu ST, Kao C (2004) Solving fuzzy transportation problems based on extension principle. Eur J Oper Res 153(3):661–674
Ebrahimnejad A (2016) New method for solving fuzzy transportation problems with LR flat fuzzy numbers. Inf Sci 357:108–124
Chandran S, Kandaswamy G (2016) A fuzzy approach to transport optimization problem. Optim Eng 17(4):965–980
Muthuperumal S, Titus P, Venkatachalapathy M (2020) An algorithmic approach to solve unbalanced triangular fuzzy transportation problems. Soft Comput 24(19):18689–18698
Das SK (2022) An approach to optimize the cost of transportation problem based on triangular fuzzy programming problem. Complex Intell Syst 8(1):687–699
Dhanasekar S, Hariharan S, Sekar P (2017) Fuzzy Hungarian MODI algorithm to solve fully fuzzy transportation problems. Int J Fuzzy Syst 19(5):1479–1491
Kaur A, Kumar A (2012) A new approach for solving fuzzy transportation problems using generalized trapezoidal fuzzy numbers. Appl Soft Comput 12(3):1201–1213
Kumar A, Kaur J, Singh P (2011) A new method for solving fully fuzzy linear programming problems. Appl Math Model 35:817–823
Singh G, Singh A (2021) Extension of particle swarm optimization algorithm for solving transportation problem in fuzzy environment. Appl Soft Comput 110:107619
Stefanini L, Sorini L, Guerra ML (2006) Parametric representation of fuzzy numbers and application to fuzzy calculus. Fuzzy Sets Syst 157(18):2423–2455
Murthy PR (2005) Operations research (linear programming), pp 155–207
Gasilov NA, Fatullayev AG, Amrahov SE (2018) Solution method for a non-homogeneous fuzzy linear system of differential equations. Appl Soft Comput 70:225–237
Gasilov NA (2022) On exact solutions of a class of interval boundary value problems. Kybernetika 58(3):376–399
Murray K, Müller S, Turlach BA (2016) Fast and flexible methods for monotone polynomial fitting. J Stat Comput Simul 86(15):2946–2966
Gasilov NA, Emrah Amrahov S (2020) On differential equations with interval coefficients. Math Methods Appl Sci 43(4):1825–1837
Acknowledgements
We would like to thank Editor-in-Chief Prof. Schahram Dustdar, Associate Editor, and the anonymous reviewers for taking the time and effort necessary to review the study. We sincerely appreciate all valuable comments and suggestions, which improved the quality of our paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kartli, N., Bostanci, E. & Guzel, M.S. Heuristic algorithm for an optimal solution of fully fuzzy transportation problem. Computing 106, 3195–3227 (2024). https://doi.org/10.1007/s00607-024-01319-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00607-024-01319-5