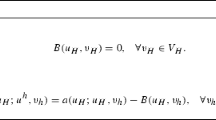p
- and hp-versions of the Galerkin boundary element method for hypersingular and weakly singular integral equations of the first kind on curves. We derive a-posteriori error estimates that are based on stable two-level decompositions of enriched ansatz spaces. The Galerkin errors are estimated by inverting local projection operators that are defined on small subspaces of the second level. A p-adaptive and two hp-adaptive algorithms are defined and numerical experiments confirm their efficiency.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.Author information
Authors and Affiliations
Additional information
Received August 30, 2000; revised April 3, 2001
Rights and permissions
About this article
Cite this article
Heuer, N., Mellado, M. & Stephan, E. hp-adaptive Two-Level Methods for Boundary Integral Equations on Curves. Computing 67, 305–334 (2001). https://doi.org/10.1007/s006070170003
Issue Date:
DOI: https://doi.org/10.1007/s006070170003