External sorting on flash storage: reducing cell wearing and increasing efficiency by avoiding intermediate writes

Abstract

This paper studies the problem of how to conduct external sorting on flash drives while avoiding intermediate writes to the disk. The focus is on sort in portable electronic devices, where relations are only larger than the main memory by a small factor, and on sort as part of distributed processes where relations are frequently partially sorted. In such cases, sort algorithms that refrain from writing intermediate results to the disk have three advantages over algorithms that perform intermediate writes. First, on devices in which read operations are much faster than writes, such methods are efficient and frequently outperform Merge Sort. Secondly, they reduce flash cell degradation caused by writes. Thirdly, they can be used in cases where there is not enough disk space for the intermediate results. Novel sort algorithms that avoid intermediate writes to the disk are presented. An experimental evaluation, on different flash storage devices, shows that in many cases the new algorithms can extend the lifespan of the devices by avoiding unnecessary writes to the disk, while maintaining efficiency, in comparison with Merge Sort.

Appendices

Appendix 1: Proofs

Proof of Proposition 1.

Proof

Consider element $A_O[i]$, where $i\le k/2$. If we do not swap $A_O[i]$ with $A_I[i]$, then $A_O[i]\le A_I[i]$. In this case, $A_O[i]$ is smaller than the elements $A_O[i+1], \ldots , A_O[k]$ because $A_O$ is sorted. Also, $A_O[i]$ is smaller than the elements $A_I[i+1], \ldots , A_I[k]$ because $A_I[i]$ is smaller than these elements due to the order of $A_I$. Hence, there are at least k elements that are greater than $A_I[i]$ in the two arrays $A_O$ and $A_I$.

If we swap $A_O[i]$ with $A_I[i]$, then before the swap the elements $A_I[i+1], \ldots , A_I[k]$ are greater than $A_I[i]$ due to the order of $A_I$. The elements $A_O[i+1], \ldots , A_O[k]$ are greater than $A_I[i]$ because they are greater than $A_O[i]$ and $A_O[i]> A_I[i]$, as a cause to the swap. Consequently, prior to the swap there are at least k elements greater than $A_I[i]$ in the two arrays, and after the swap this holds for $A_I[i]$.

Based on the above two cases $\{A_O[1], \ldots , A_O[k/2]\}\subset S$. Similar arguments can show that for every element among $A_I[k/2], \ldots , A_I[k]$ there are at least k elements smaller than it, and hence, $\{A_I[k/2], \ldots , A_I[k]\}\cap S=\emptyset$.

Finally, we show that after the swaps the arrays are sorted. Consider $A_O[i]$ and $A_O[i+1]$, for some $1\le i \le k-1$. Before the swapping phase, $A_O[i]\le A_O[i+1]$, since $A_O$ is initially sorted. Thus, if none of them is swapped, $A_O[i]\le A_O[i+1]$ holds. If both $A_O[i]$ and $A_O[i+1]$ are swapped, then the claim holds because $A_I$ is initially sorted, so $A_I[i]\le A_I[i+1]$. If just $A_O[i]$ and $A_I[i]$ are swapped, then $A_I[i]<A_O[i]$, so $A_I[i]<A_O[i]\le A_O[i+1]$, so the claim holds. If just $A_O[i+1]$ and $A_I[i+1]$ are swapped, then $A_O[i]\le A_I[i]$, because they were not swapped and $A_I[i]\le A_I[i+1]$ because $A_I$ is sorted, thus $A_O[i]\le A_I[i+1]$ before the swap and the claim holds. Similar arguments show that $A_I$ is sorted after the swaps. $\square$

Proof of Lemma 1.

Proof

The union of two different MSCs is not an MSC because otherwise it would contradict maximality—each MSC is a proper subset of the union but cannot be a proper subset of an MSC. The intersection of any two MSCs is an empty set because otherwise their union would be an MSC, in contradiction to the previous statement. $\square$

Proof of Proposition 2.

Proof

To prove the existence of a partition, consider the following recursive process. When given a sorted (ascending) sequence, return as a partition a set comprising this sequence. When given a sequence $t_1, \ldots , t_m$ that contains two consecutive tuples $t_j$ and $t_{j+1}$ such that $t_j[K] > t_{j+1}[K]$, apply the process recursively on $t_1, \ldots , t_j$ and $t_{j+1}, \ldots , t_m$ and return the union of the partitions that were computed by the recursive calls.

Table 4 I/O rates of flash storage devices

The recursive process provides a partition of R because tuples of R are never discarded or duplicated in the process. Hence, the created sets are disjoint and cover R. Obviously, every set in the result is a sorted sequence, since otherwise it would have been partitioned. Maximality follows from the fact that the partition is always into sequences $t_1, \ldots , t_j$ and $t_{j+1}, \ldots , t_k$ such that $t_j[K] > t_{j+1}[K]$; thus, extending each such sequence disobeys the order.

To show that a partition is unique, suppose there were two different partitions of R into MSCs. Then there would be a tuple t such that t is in one MSC of the first partition and in a different MSC of the second partition. In this case, the intersection of two different MSCs is not empty, since it contains t, in contradiction to Lemma 1. $\square$

Proof of Proposition 3.

Proof

(Sketch) For two tuples $t_i$ and $t_j$ that are in the same MSC, their order is the order in the MSC, and hence, it is according to the sort key.

If $t_i$ is in $M_i$, $t_j$ is in $M_j$ and there is an edge from $M_i$ to $M_j$, then $M_i$ precedes $M_j$. Suppose $M_i$ totally precedes $M_j$. Let $t^{\prime }_i$ be the last tuple of $M_i$ and $t^{\prime }_j$ be the first tuple of $M_j$. Then, $t^{\prime }_i[K]\le t^{\prime }_j[K]$, and thus, $t_i[K]\le t^{\prime }_i[K]\le t^{\prime }_j[K]\le t_j[K]$. Suppose $M_i$ overlaps and precedes $M_j$. Let $(t^{\prime }_i, t^{\prime }_j)$ be the connectors of $M_i$ and $M_j$. Then, $t_i[K]\le t^{\prime }_i[K]\le t^{\prime }_j[K]\le t_j[K]$.

The rest of the proof is by induction showing that if $t_i$ is in $M_i$, $t_j$ is in $M_j$ and there is a path in $G_R$ from $M_i$ to $M_j$, then $t_i[K]\le t_j[K]$. The induction is on the length of the path where the case of $M_i$ and $M_j$ that are connected by an edge is the basis of the induction. $\square$

Proof of Proposition 4.

Proof

From Proposition 3 follows that the underlying sequence of $P_b$ is a sorted sequence. Given a sorted subsequence of R, comprising $t^{\prime \prime }_1, \ldots , t^{\prime \prime }_{k^{\prime \prime }}$, we partition it by assigning each tuple to the MSC that contains it. Recall that the partition into MSCs is unique (Proposition 2). Let $M_{i_1}, \ldots , M_{i_n}$ be the MSCs to which we assigned tuples of the given sorted subsequence. Each pair of consecutive tuples $t^{\prime \prime }_i$, $t^{\prime \prime }_{i+1}$ in the subsequence, satisfies one of the following cases. (1) Tuples $t^{\prime \prime }_i, t^{\prime \prime }_{i+1}$ are in the same MSC. (2) Tuples $t^{\prime \prime }_i, t^{\prime \prime }_{i+1}$ belong to MSCs $M_i$ and $M_j$ such that $M_i$ totally precedes $M_j$. (3) Tuples $t^{\prime \prime }_i, t^{\prime \prime }_{i+1}$ belong to MSCs $M_i$ and $M_j$ such that $M_i$ overlaps and precedes $M_j$. One of these cases must hold. If Case 1 does not hold, $t^{\prime \prime }_i$ and $t^{\prime \prime }_{i+1}$ are tuples in two different MSCs such that $t^{\prime \prime }_i$ appears in R before $t^{\prime \prime }_{i+1}$ and $t^{\prime \prime }_i[K]\le t^{\prime \prime }_{i+1}[K]$. In this case, either the MSCs do not overlap (Case 2) or overlap (Case 3). Thus, $t^{\prime \prime }_1, \ldots , t^{\prime \prime }_{k^{\prime \prime }}$ yields a path in $G_R$. The MSCs $M_{i_1}, \ldots , M_{i_n}$ are, therefore, part of a path in $G_R$. Since the weight of this path is smaller than the weight of $P_b$, it holds that the number of tuples in $t^{\prime \prime }_1, \ldots , t^{\prime \prime }_{k^{\prime \prime }}$ does not exceed the number of tuples that $P_b$ comprises. $\square$

Appendix 2: I/O rates

To illustrate the performances of the storage devices on which we ran the tests, we used CrystalDiskMark ²—a well-known hard drive benchmark.

We performed four different tests on our devices, to examine their characteristics: (1) Sequential read test—4 GB of data were read from the device sequentially, the block size was 1024 KB. (2) Sequential write test—4 GB of data were written to the device sequentially, the block size was 1024 KB. (3) Random read test—4 GB of data were read from the device from random addresses, the block size was 512 KB. (4) Random write test—4 GB of data were written to the device in random addresses, the block size was 512 KB. The tests were performed ten times, the average results were taken, and the rate was calculated. The results are presented in Table 4.

Table 4 shows that the HDD reading rates are almost equal to the writing rates (for both random and sequential accesses). This is non-surprising as there is no difference between reading and writing in HDD. Note that in HDD the writing rates are a little bit better than the reading rates. This is due to the buffering mechanism, which in this benchmark we could not control (as opposed to our experiments). The random I/Os are less efficient than the sequential I/Os, on HDD, due to the large seek time in random access, relatively to the access times in sequential access.

As opposed to the sequential and random read rates of the HDD, we can see that the sequential and random read rates are similar in both SD Card and Micro SD Card. According to [1], the read performances depend on the block size, but usually not on whether the access pattern is random or sequential. We can also see that the sequential read rate is higher than the sequential write rate, in both devices.

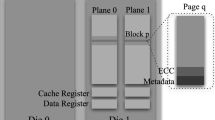
We can see that the SSD performances are good relatively to the other devices. The SSD optimizes the performances in two different levels. (1) An hardware level parallelism is used to perform read, write and erase operations on different planes independently. (2) On the firmware level, the controller of the SSD optimizes the I/O operations while using the garbage collector to erase blocks, as a background process and not immediately. Table 4 shows that the random write performance is relatively poor due to write amplification caused by garbage collection. When writing randomly, the overhead of moving valid pages to other blocks leads to write amplification, which increases the required bandwidth and shortens the time during which the SSD reliably operates [27]. The sequential read rate is slightly better than the random read rate, due to optimizations performed by the controller.